elementaar
Mitglieder-
Gesamte Inhalte
1.404 -
Benutzer seit
-
Letzter Besuch
Inhaltstyp
Profile
Forum
Kalender
Articles
Alle erstellten Inhalte von elementaar
-
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Noch ein Z, aber ein doppeltes. -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Die Maßeinheit der Z-Wertes ist σ (Standardabweichung). -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
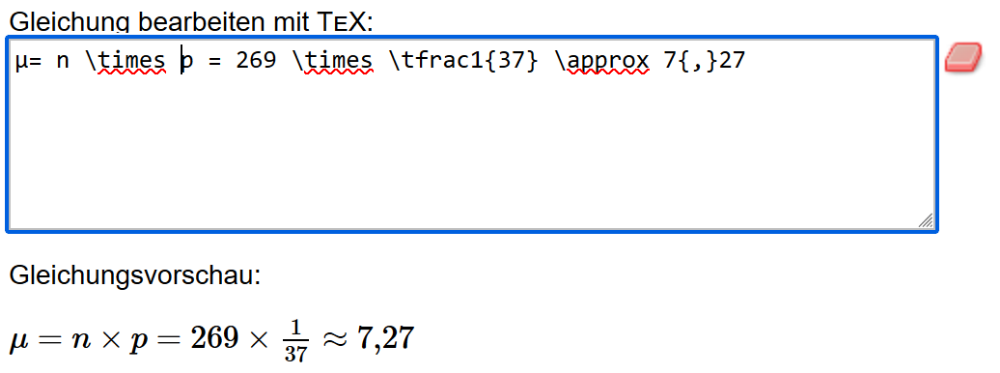
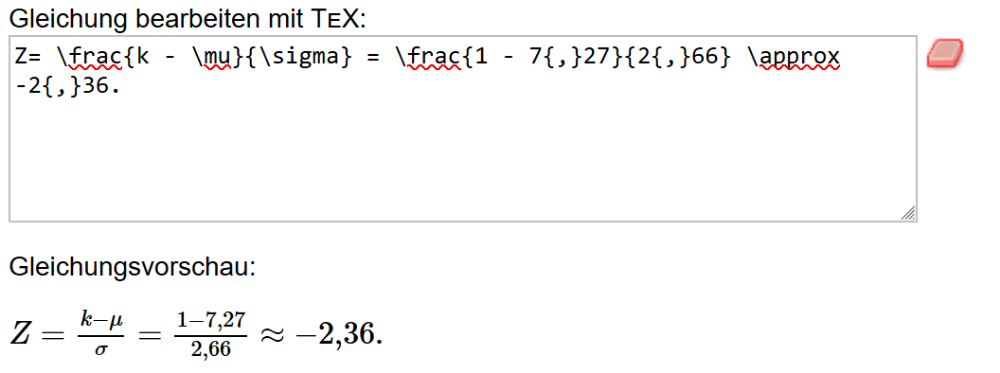
Wozu soll das jetzt gut sein? SEINE bornierte Ignoranz und kaum unterbietbare Dummheit ist auch im letzten 7er-Beitragswüten prächtig zum Ausdruck gekommen. Wozu jetzt die neue Staffel? ER sollte SEINEM "math. " vielleicht nicht alles blind glauben?! So oft wie der falsch liegt. Extra für IHN übersetzt: Erwartungswert mit p=1/37 und 269 Coups: Varianz dazu: ergibt Standardabweichung: ergibt mit K=1 und 269 Coups eine Abweichung (Z): Ich kann nichts dafür, daß man das in dieser Welt so und nicht anders berechnet. So sind die Tatsachen. Und wenn IHM das nicht passt, ist das SEINE falsche und deshalb irrelevante Privatmeinung. Warum belästigt ER unschuldige Forenbesucher fortgesetzt mit SEINEM Humbug? -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Dem selbst erklärten know-it-all den Z-Wert erklären zu müssen, ist allein schon lustig - aber danke für die solide Zusammenstellung. Vor allem: wenn sorgfältig zubereitet, dann schmeckt es auch. SEINE Reaktion allerdings ist, selbst für SEINEN beschädigten Gehirnapparat, erstaunlich. Aber nicht doch. Das entfesselte Formelschreiben des noch tiefer Denkers ist nach wie vor eine unterhaltsame Augenweide. Mit einer Wirkung auf IHN, die fast dem Trinkspiel gleichkommt. Mit den Worten eines bekannten Zeitgenossen: "Und dann hat er gesagt... hihi... er ist... entfesselt" Aber warum denn? ER stellt doch bloß wieder SEINEN liebsten Zeitvertreib aus: SEINEN "math. " bescheuerten Unsinn verlautbaren lassen, um dann grundlos andere Leute zu beschimpfen und zu beleidigen. Wie eine Zahl innerhalb von 37 Coups 268 mal ausbleiben kann, wollte ER wohl nicht erklären (daher die Verbesserung in SEINEM Ursprungsbeitrag, natürlich ohne Korrekturnotiz, aber mit nachfolgender Zitatfälschung.) Und wie kommt ER, als längst Disqualifizierter, zu der Annahme, ER bräuchte bloß zu Toben und zu Schreien, damit IHM jemand die einfachsten Rechenschritte "erklärt"? Wo ER doch regelmäßig schon am Zählen und Addieren scheitert? Hinweis: das bedeutet, ganz praktisch, das Wort "disqualifiziert": es findet sich, außer der KI, niemand mehr, der seine Lebenszeit mit SEINER Spiegelfechterei verschwendet. Denn am Ende, wenn IHM gar kein Ausweg mehr bleibt, wird ER die ganze Rechnerei sowieso für "wurscht" erklären (fakultativ noch "schwülstig" und "Zahlengedöns" verwenden). . (Sätze werden im Schriftdeutschen mit einem Punkt abgeschlossen.) Daß es hier noch Mitleser geben könnte, die diese Selbstbeschreibung wirklich benötigen, ist hoffentlich ganz irreal. Wenn selbst die von IHM so ausdauernd geschmähte KI in der Lage ist, den richtigen sigma-Wert bekannt zu geben (und daß er richtig ist, muss man selber ausrechnen, wenn man es denn kann; ER kann es ja offensichtlich nicht), sollte klar sein, wer hier mit weitem Abstand der Oberblödmann ist. Auge, Splitter und Balken... nicht nur für Fische erwägenswert. -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Neue köstliche Kostprobe vom "math. ". EZ (Plein) Rotation = 37 Coups. Aber "35" bleibt (solitär?) innerhalb von 37 Coups zu 1% dafür aber 268 Coups lang weg. Der richtige Sigmawert ist -2,358. Ich geh' dann mal Wurschtbraten, aber schnurz. -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Das stimmt (wahrscheinlich). Da sei der "math. " vor. Kein denkender Mensch möchte SEINE Art verstehen, weil sie in diesem Universum zu nicht brauchbaren Ergebnissen führt. Unter heftigem Gelächter biegen sich weiter die Balken (brechen die irgendwann, oder gilt das nur für zum Brunnen pilgernde T(r)öpfe?) Beleg für diese Worte? Auf SEINEM Platz ganz gewiß nicht, dort ist der verfügbare Platz flächendeckend und meterdick von SEINER Lügerei belegt. Aber das ist ja alles sowieso "wurscht". (Hinweis: Unterstrichene Worte sind sogenannte "Links". Ein Klick darauf führt manchmal zu erhellenden Fußnoten.) -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Danke für diesen Hintergrundbericht, @Feuerstein. Das fehlende Excel auf SEINEM Rechner hielt ich damals für die unverschämte, aber lustige Pointe der Diskussion (ER hätte ja auch einen der diversen online-Dienste zum Betrachten verwenden können, bevor ER SEIN lächerliches Verdikt von der "Falschheit" ablässt). Aber daß Du IHN per PN, also eher vertraulich, in den ersten Tagen mit nachprüfbaren Belegen SEINER Fehler versorgt hast, macht die Sache ja noch irrer und wirklich ärgerlich. Die von IHM so vehement geforderten Beleglinks in meiner Tabelle hätte ich mir also sparen können, da ER sowieso entschlossen war, nichts davon überhaupt zur Kenntnis zu nehmen. SEINE Dummheit ist zuweilen nervtötend, aber kein adäquater Gegenstand für Spott, SEINE ständige Lügerei allerdings... SEIN Gewinnsatz à 100, mit Geld, was ER gar nicht mehr zur Verfügung hatte, ist im Übrigen das Hunderfache SEINER Anfangssätze: vom 02.01. bis zum 09.01. war SEINE Satzhöhe ausschließlich à 1 (Klick auf die erste Seite dieses Themas zeigt die Belege). Gruss elementaar -
Ganz genau. Schönes Wochenende! elementaar
-
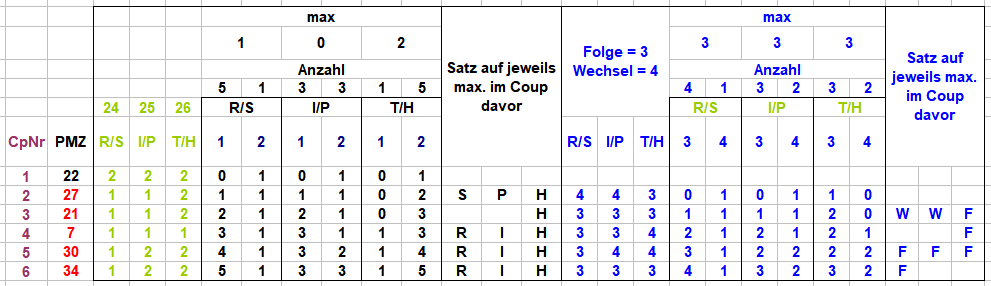
Hallo @Feuerstein, das war für mich schon beim Formulieren eine Hürde, wie das möglichst kurz und knapp in Worte zu bringen sei. Gemeint ist: beginnend mit dem 1. F2 (beispielsweise "26") wird der Zeitpunkt des 1. F3 festgestellt. Es dauert, beispielsweise, 15 Coups bis der 1. F3 erscheint. Ist der 1. F3 "26" wird ein Treffer gezählt, und unter "max" wird "15" eingetragen. Ist der 1. F3 aber eine andere Zahl als "26", beispielsweise "27", wird unter "max" wieder "15" eingetragen, aber natürlich kein Treffer gezählt, der 1. F2 war ja nicht der 1. F3. Dauert es im nächsten Versuch beispielsweise 17 Coups bis nach dem 1. F2 der 1. F3 erscheint, wird in Spalte "max" die dort stehende "15" mit "17" überschrieben. Die Spalte "max" verzeichnet also nur, wie lange es höchstens gedauert hat, bis nach dem Erscheinen des 1. Fx der 1. Fx+1 erschienen ist, ohne daß das eigentliche Spiel (Fx = Fx+1) zwangsläufig mit einem Treffer abgeschlossen wird. Im Beispiel ginge es mit "27" als 1. F3 weiter bis zum 1. F4, der wieder "27" oder eine andere Zahl sein kann. In Kapitel 3 ist eine Verfolgung bis zum Treffer (aber nur bis F20) abgebildet. Gruss elementaar
-
1. F2 bis 1. F100; 102.400 Versuche. EZ_Wie oft ist Fx = Fx+1 - 1. F2 bis 1. F100 Zus01.pdf Gruss elementaar
-
Sehr bedauerlich. Mir ging's mal so mit einer Stange aus Griechenland (Mitbringsel, Oma hat's gut gemeint). Beim Rauchen ständig den aufkommenden Brechreiz bekämpfen zu müssen. Will ich nie wieder haben. Meinst Du die? Quelle: http://www.tabakpfeife24.de/Zigaretten-Feinschnitt/Zigaretten/A-G-Zigaretten-Marken/Afri/Afri-Filter-Zigaretten.html Die kommen auch von van Landewyck. Bekannt ja, selbst geraucht: nein. Ist mir da etwas entgangen? Gruss elementaar
-
Interessante Umfrage. Ich bin wirklich froh und dankbar, daß ich die Vielfalt an Geschmack und Stärke, wie sie in den 1980ern noch möglich war, erleben konnte, bevor sie eine entfesselt geisteskranke EU-Bürokratie unter dem Vorwand der "Gesundheit" in einen kaum noch genießbaren Einheitsbrei pervertiert hat. Damals gab es noch Zigaretten, die von sehr leicht bis sehr stark, von licht und hell bis tief und dunkel die unterschiedlichsten Geschmäcker befriedigen konnten - und das auch noch in unterschiedlichen Ländern zur selben Marke mit unterschiedlichen Mischungen. In der Zeit bin ich regelmäßig nach Frankreich gefahren, weil mir meine damals bevorzugten Zigaretten Benson & Hedges in der französischen Mischung besser als in der deutschen schmeckten. "Silk Cut", sehr scharf, beim Inhalieren bleibt fast der Atem stehen, "Lambert & Butler", sehr befriedigend zwischendurch, oder die damals neu lancierten "Davidoff", sensationell, wie eine Zigarette auch schmecken konnte. Aber auch die originalen, relativ simplen "Gauloises" oder "Gitanes" ohne Filter. Ausgeprägte Charaktere. Alle, wenn noch existent, nur noch ein schaler und schmerzlicher Abglanz vergangener Zeiten. Wirklich verrückt, wozu einen staatliche Übergriffigkeit im Verein mit allzu willfähriger Industrie treiben kann: seit Anfang des Jahres mische ich mir meinen Zigarettentabak selbst. Aktuell: 17 Gewichtsteile (van Landewyck) Ducal 11 Gewichtsteile (von Eicken) Pepe Rich 12,1 Gewichtsteile (Peterson) Early Morning Pipe (früher: Dunhill; vor dem Untermischen kleiner häckseln) Seitdem macht das Zigarettenrauchen wieder richtig Spaß. Der zusätzliche Zeitaufwand ist es mir dicke wert. Gruss elementaar
-
VPS-EC-Figuren-Scanner (das Original)
topic antwortete auf elementaar's Mark Wendor in: Roulette-Systeme
Vielen Dank für Fundstück, Übersetzung und Analogie - besonders liest sich wie eine vollständige Beschreibung meines Selbst: wann immer etwas, auch nur von Ferne, nach Arbeit aussieht, nehme ich die Beine in die Hand (also jetzt nicht buchstäblich, das sagt man nur so, auch den Lunch, getrunkener Weise, nicht zu vergessen) und renne, so schnell ich nur kann, woanders hin. Klappt oft; wenn aber, heimtückisch, dort auch Arbeit lauert, kommt man schnell aus dem Schnauf. -
Du findest aber auch wirklich ALLES (nach wie vor unvergessen: die Apfel-Würstchen-Platte zweifelhafter Appetitlichkeit), und schaust dennoch nicht auf uns andere herab: das nenne ich wahre Noblesse. Danke. 3,49€ geteilt durch 3l = 1,16€/l (extra abgerundet). 2,95€ geteilt durch 1,16€/l = 2,543l (€ kürzt sich weg; nochmal extra abgerundet). Das sollte zum Mittagessen reichen?
-
VPS-EC-Figuren-Scanner (das Original)
topic antwortete auf elementaar's Mark Wendor in: Roulette-Systeme
Hallo @chris161109, mit Deinem hast Du einen Flecken tabula rasa meiner Bildung aufgedeckt. Tatsächlich hatte ich bis hierhin noch nie von dieser, wenn man's sich lebhaft vorstellt, doch ziemlich beunruhigenden Geschichte gehört. Vielen Dank! Gruss elementaar -
Hallo @Paroli, vielen herzlichen Dank! Es ist mir durchaus bewusst, daß solche Ansinnen wie meines Dir zusätzliche Arbeit verursachen, und mein Fehler in der Blödheitsskala ziemlich hohe Punktwerte erzielt - erklärlich (nicht entschuldigt) dadurch, daß ich gar nicht so intensiv in das Thema einsteigen, sondern bloß eine Handreichung geben wollte, und darüber die simpelste Plausibilitätsprüfung unterließ. Die beste Absicht ging gründlich schief. Danke auch für den PN-Hinweis - bisher ging ich davon aus, daß, wenn man den Forennamen als Link schreibt, dies den Adressaten "wie von Zauberhand" auch erreicht. Danke nochmals! Gruss elementaar
-
Hohoho, da muss ich aber mal in die Präche gretchen. Also der Hans, der ist gar kein Fuffziger, aber gar und nimmer nicht, der ist @Hans Dampf (von!!!) und ohne ihn ginge hier ja gar nichts. Kraht hat er wieder was außengegrappen und als ich geleßt, was da stand - plattgold, von wegen! die buren Bahren davon in der Texteröte. Baggerfahren, gut, aber ob heut noch Zugfahren, sogar abgefaaren bei DER Bahn, daß klaup erst wenn mit eiknäm Auk erblickt. Und pasta! kenn wir all vom cornifähre. Abar 1 stiehmt: Unhöflich nicht gutt. Gruss elementaar
-
O ja, das würde ich auch bedauern. Ich bin zwar noch nicht wieder ganz bei mir, nach meinem Ausflug ins Ätherische, doch was ich da erblickte, ich kann Dir sagen... Diese amöbenhafte Gestaltverwandlung der Schablone in Live (kann man das sagen?) ist ein Erlebnis, was dringend auf das Roulettespiel übertragen werden muss. Ein Forschungsfeld sehr variabler Begrenzungen. Aber wie ist das mit dem Volumen? Mit neuer Zuversicht hoffe ich auf künftige Beiträge. Gruss elementaar (fast wieder ein einziger)
-
Hallo @Feuerstein, @Hans Dampf (von) & Copilot und natürlich @Chemin de fer, vielen Dank für Eure Enträtselungsvorschläge. Das weiß ich zu schätzen. Meine ziemlich eindeutige Sympathie liegt dabei im Metamorphischen. Das größte Gelächter hat allerdings Copilot bei mir ausgelöst (vielen Dank, fast noch besser als Formeln schreiben), der adhoc eine Betrachtungsweise erfindet, für die es in den Texten von @Maitre keinen Beleg gibt, und die im Ergebnis einen solch herrlichen Unsinn produziert, daß er in den vernebelnden Worten fast nicht mehr erkennbar ist - vielleicht hat er sich ja die Schrödinger-Wittgensteinsche Interpretationsfalle von @Ropro zu Herzen genommen. Vorwitzige Zwischenfrage: Wenn wir an "Position 1" flexibel "Rot" spielen sollen, müssen wir ja hoffen, daß ein ganzer "6er-Block" ohne vorherige "Musterverzerrung" durch einen zu früh erscheinenden F2 vor uns liegt. Ist das eine begründete Hoffnung? Oder ist das eben das Risiko? Zu welch imposanten Leistungen man sich durch stetiges Üben emporschwingen kann, zeigt diese Nebenbeibemerkung: Hast Du damit noch Schwierigkeiten? Übungssache. Mittlerweile mache ich solche Kleinigkeiten nur mehr im Kopf, die Hände brauche ich zum Lunch. Nahezu unglaublich! würde ich spontan sagen, wenn der Zeuge nicht so zuverlässig wäre. Respekt. Da bleibt mir eigentlich nur, für ein kleines Stündchen, das Schnüffeln am Ätherfläschchen. Erwartung (ohne Wert): Studium der morphischen Schablonenveränderung, aber möglichst meta! Gruss elementaar
-
Als ich genau das tat und veröffentlichte, war's ein Missverständnis und nicht richtig und ungenau. Der Coupsverbrauch für 100.000 Versuche war 832.349 Coups (inklusive erstem F2; 732.349 ohne diesen), mit echten und wahren Zufallszahlen, nicht den falschen. Ein Landcasinotisch bräuchte dafür knapp acht Jahre. Ist aber alles obsolet, ich seh's, ganz ohne Groll, ein: ohne die Schablone geht es nicht. Insofern: weiter frohes Schaffen! elementaar
-
Bitte, gern. Leider dürfte sie aber, laut Wortmeldung von @Maitre, auch nicht dem Gemeinten entsprechen. Ging es am Anfang um die "Farben" der EC, und wann und wie gezählt der Scheitelpunkt beim F2 ist, geht es jetzt um Folge-Wechsel, bei dem dann noch ein Vorlaufcoup benötigt wird und "Zéro" plötzlich nicht mehr mitspielt. Das ist so "kompliziert", daß die nächsten "Missverständnisse" sich sehr schnell einstellen werden. Eines dieser Missverständnisse ist sogar schon eingetreten: Mein viel zu einfach gestricktes Hirn musste schon mehrmals, mit steigendem Energieaufwand, den (wahrscheinlich ganz falschen) Eindruck bekämpfen, veräppelt zu werden. Deshalb bin ich jetzt hier raus. Gruss elementaar
-
Wie gehabt ist ER zu sinnerfassendem Lesen zu faul oder zu dumm, muss aber dennoch SEINEN irrelevanten Unsinn ablassen. Ich mache @Paroli für überhaupt nichts verantwortlich, es ist sein Forum und er handelt, wie es ihm passt. Da gibt es für mich nichts zu diskutieren. Welche Schlüsse ich für mich und mein Verhalten daraus ziehe, unterliegt weder SEINEM noch @Parolis Willen. Wieder für mich: Ende der Diskussion. Es ist sehr schade, daß man hier mittlerweile Selbstverständlichkeiten ausbuchstabieren muss. Dazu fehlen mir Zeit und Antrieb. Tatsachenfeststellung! Ende der Diskussion.
-
-
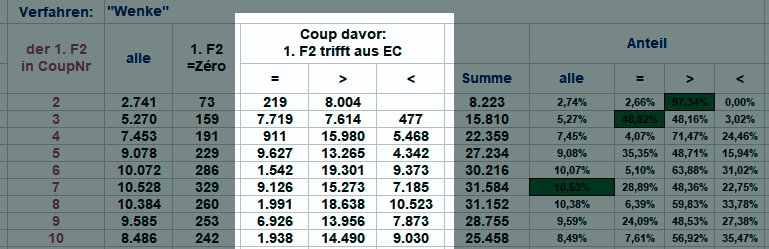
Hallo @Maitre, vielen Dank für Deine erläuternden Worte. Ich darf vielleicht Deine Aufmerksamkeit auf die Spalten 4 bis 6 meiner Tabelle hinweisen: Wer möchte, kann also mit der Tabelle per einfacher Kettenrechnung für jeden Coupzeitpunkt ausrechnen, was er hätte setzen müssen, und welches Ergebnis er erzielt hätte. Nicht ablesbar ist, ob und welche Unterschiede es gibt, wenn eine, zwei oder alle drei EC ein Über/Untergewicht haben. Auch das habe ich untersucht, sehe aber von einer Veröffentlichung ab, da ich mit der ersten Tabelle schon in die falsche Datei gegriffen habe, und aus der Nichtreaktion von @Paroli schließen muss, daß es sowieso keine Rolle spielt, ob hier etwas richtig oder falsch ist. Gruss elementaar