elementaar
Mitglieder-
Gesamte Inhalte
1.436 -
Benutzer seit
-
Letzter Besuch
Inhaltstyp
Profile
Forum
Kalender
Articles
Alle erstellten Inhalte von elementaar
-
Hallo Hans Dampf, Merci. Ein Spiel, bei dem Zéroteilungen vorkommen, sollte eigentlich immer besser abschneiden, als eines, wo dies nicht geschieht, eben weil man bei jedem Erscheinen von Zéro etwas weniger verliert als auf den anderen Chancengrößen. Erwartet wird also irgendetwas größer als -2,7%. Es hängt dann davon ab, wie groß der Anteil des EC-Satzes am Gesamteinsatz ist, wie stark die Verlustverkleinerung ausfällt. Statt es auszurechnen, habe ich es einfach ausprobiert. Ich finde, Dein zweiter Wurf schlägt sich ganz beachtlich, bei 100% Trefferwahrscheinlichkeit. Gruß elementaar
- 451 Antworten
-
- oc
- online-casino
-
(und %d Weitere)
Getaggt mit:
-
Hervorhebung von mir. Das ist u.a. die Teilbegründung dafür, warum das Rechenmodell von @Alter Schwede zwar formal einleuchtet, in der Praxis jedoch, leider, zunächst nicht weit führt.
- 451 Antworten
-
- oc
- online-casino
-
(und %d Weitere)
Getaggt mit:
-
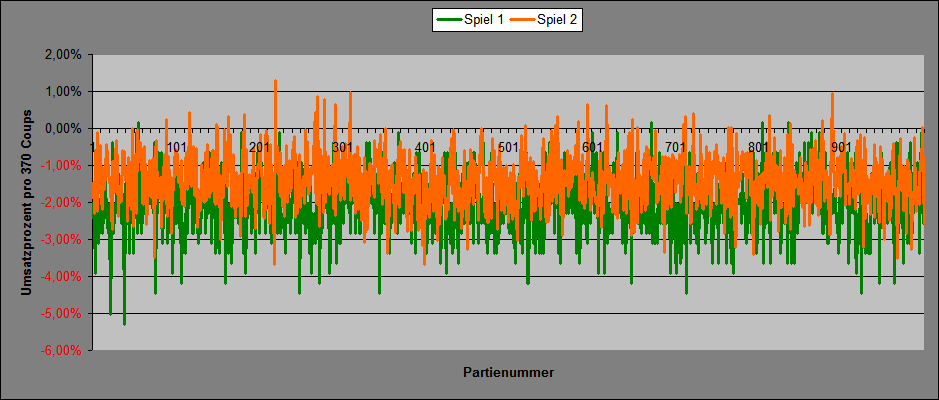
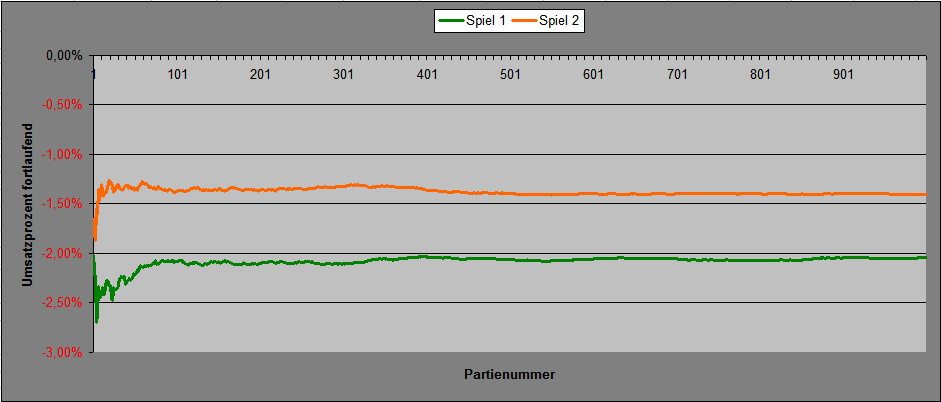
Hallo Hans Dampf (100%), als Ergänzung: ich habe das erste Satzmuster "Spiel 1" genannt. Einsatz pro Coup 143 Stück Jeder Coup gewinnt +1 Stück, außer bei Erscheinen von "18", dann -143 Stück. Analog das zweite Satzmuster "Spiel 2". Jeder Coup schließt mit -1 Stück ab, außer bei Erscheinen von: "0", dann 0 Stück, oder "1", "2" oder "3" dann +8 Stück. Untersucht wurden Permanenzstücke zu je 370 Coups (Verfahren "Wenke"). Umsatz für die Strecke: Spiel 1: 370 x 143 = 52.910 Stück Spiel 2: 370 x 17 = 6.290 Stück Das habe ich 1.000 mal wiederholt. Diagramm 1 zeigt die jeweils nach 370 Coups Spieldauer erzielten Umsatzprozent. Diagramm 2 zeigt die Umsatzprozent bei jeweiliger Fortschreibung und Addition der getätigten Umsätze und Saldostände. Umsatz für die Gesamtstrecke: Spiel 1: 370 x 143 x 1.000 = 52.910.000 Stück Spiel 2: 370 x 17 x 1.000 = 6.290.000 Stück Endergebnis für die Gesamtstrecke: Spiel 1: 370 x 143 x 1.000 = -1.080.088 Stück, entsprechend -2,04% Spiel 2: 370 x 17 x 1.000 = -88.437 Stück, entsprechend -1,41% Von 1.000 Spielstrecken à 370 Coups wurden mit Saldo > 0 abgeschlossen: Spiel 1: 4, entsprechend 0,40% Spiel 2: 30, entsprechend 3,00% Angesichts der Ergebnisse ist mir auch wieder eingefallen, daß ich Spiel 1 damals beim Thema "Schwankungsbreite" quasi als Modell und "Spiegelung" mitlaufen ließ. Gruß elementaar
- 451 Antworten
-
- oc
- online-casino
-
(und %d Weitere)
Getaggt mit:
-
Hallo 100%Hans Dampf, den Titel hast Du Dir redlich verdient - das wird ja ein richtiger Lauf! Außerdem bringst Du mich zum Staunen, mit den Möglichkeiten, die das partielle Mehrfachbelegen von Zahlen bietet. 1a und Respekt! Danke nochmals, elementaar
- 451 Antworten
-
- oc
- online-casino
-
(und %d Weitere)
Getaggt mit:
-
Hallo Hans Dampf, vielen Dank für's Bekantgeben. Ich hatte dunkel 147 Stück im Kopf, und bekam es nicht mehr zusammen. Bei Deinem Vorschlag sind es also 143 Stück pro Coup. Was mich jetzt aber wirklich interessiert: tatsächlich dauerhaft schlechter als minus 2,7% ? Ist das so eine Art Zwei-Dutzend-Ding? Allerdings so richtig, richtig interessant wäre es, wenn er schlechter als -5,4% abschneiden könnte. Habe ich vormals vielleicht zu schnell abgetan. Schaue ich mir vielleicht doch noch einmal an. Zum Thema paßt es allerdings auf alle Fälle. Danke! Gruss elementaar
- 451 Antworten
-
- oc
- online-casino
-
(und %d Weitere)
Getaggt mit:
-
Hallo Hans Dampf, ehrlich, ich ahnte das schon, daß Du noch mehr Tricks auf Lager hast. Aber mit der schönen 100% Trefferwahrscheinlichkeit ist es dann, wenn ich recht sehe, Essig. Andererseits, wenn man darüber einige der 370 x 767 Billionen Scheinspieler einsparen könnte, wäre es eine Überlegung wert, die sind halt doch ein unruhiger Haufen... Glückwunsch auch für Deine Millionen, die @suchender Dir andichtet. Gruß elementaar PS.: Wie ich sehe, Schade, die Millionen sind schon weg.
- 451 Antworten
-
- oc
- online-casino
-
(und %d Weitere)
Getaggt mit:
-
Was für eine ausgezeichnete Idee! Bravo. Ich fürchte allerdings, besser und vor allem unterhaltsamer als der Kollege "overfly" aus dem entschwundenen, anderen Forum wird das in diesem Leben keiner mehr machen können.
-
Mal noch ein Gedankenspiel zum Thema (Absurditäten sind beabsichtigt und dienen, hoffentlich, der Verdeutlichung): will man 100% Treffsicherheit im nächsten Coup gibt es nur einen möglichen Weg: alle Möglichkeiten zeitgleich setzen. Dabei verwenden wir den Satztrick von @Hans Dampf : 18 Stück auf Passe, 18 Stück auf Manque 1 Stück auf Zéro. Klar, in 36 Fällen verlieren wir, trotz sicherem Treffer, unser einkalkuliertes eine Stück. An einem Tisch mit Zéroteilung gibt es aber den einen, für uns günstigen Fall (das weiß nicht jeder!), nämlich wenn Zéro fällt. Dann ist Erntezeit mit fetter Beute: nicht nur 36 Stück Pleinauszahlung, hinzu kommen ja noch 2x9=18 Stück aus den beiden Zéroteilungen. Gesamtauszahlung 54 Stück; viel mehr als wir eingesetzt haben, super, wer sagt's denn, wir sind die ausgemachten Roulettekings (in unserem Freudentaumel vergessen wir den Tronc, geschieht denen aber auch recht, die haben uns ja vorher 36 mal geradezu abgedreht). Da wir aber Systemiers sind, und da ist Disziplin ja mit das Wichtigste (hört man immer wieder: nur ja nicht in wilde Zockerei verfallen, wenn es mal nicht so läuft, immer an das System halten!), gehen wir natürlich nicht an irgend einen Tisch und spielen einfach so drauf los, nein, wir setzen nur, wenn wir auch dürfen, nämlich, wenn vorher in 37 Coups auch wirklich 37 verschiedene Zahlen gefallen sind. Laut Tabelle (ohne die geht ja schon mal gar nichts!) findet das Ereignis innerhalb von rund 767 Billionen Versuchen statt. Das ist natürlich ziemlich selten. Kann uns, zumal in den heutigen Zeiten, aber gar nicht abschrecken: der zweite Trick (jetzt kommt's!) sind die Scheinspieler: wir richten einfach 767 Billionen Scheinspieler ein, dann dürfen wir, im Durchschnitt, jeden Coup setzen. Aber Moment, was ist mit den Schwankungen? Durchschnitt heißt ja nicht, daß wir wirklich jeden Coup spielen dürfen! Puh, ist das anstrengend. Kann uns aber gar nicht aufhalten: wir richten einfach 37 x 767 Billionen Scheinspieler ein, damit erhöhen wir auch die Chance, daß einer davon Zéro trifft. Super. Aber Zéro schwankt in ihrem Erscheinen ja auch. Lieber auf Nummer Sicher gehen: wir richten 370 x 767 Billionen Scheinspieler ein, da sollte aber wirklich nur in absolut seltenen Ausnahmefällen (vom Betrug des Tischbetreibers zu schweigen) bei keinem der satzreifen Scheinspieler die Zéro nicht fallen. Der eventuell nötige Differenzsatz (noch so ein Trick!) ist da nur noch ein Klacks. Soweit gerüstet, treten wir, reinen Gewissens und mehr als bereit, wirklich ganz groß abzusahnen, an den Tisch. Man stelle sich das mal vor: 370 x 767 Billionen Scheinspieler! Die üben einen solchen (man könnte fast sagen: Quanten!-) Druck aus, das kann gar nicht lange dauern, bis Zéro fällt. Und dann gewinnen wir ohne Ende! =========== Warum, bei anderer Betrachtungsweise, die 100% Trefferwahrscheinlichkeit in Coup 38 ein kaum überbietbares Desaster für den Spieler sind, darüber rentiert es sich, ein paar Überlegungen anzustellen. Einige Schlagworte reichen da nicht aus. =========== Das über das doch rechtschaffen öde Thema mit der Rechnerei Hinausweisende hat @Egoist im anderen Thema hier geschrieben: https://www.roulette-forum.de/topic/18595-789-besser-als-24/page/4/?tab=comments#comment-403947 Gruß elementaar
- 451 Antworten
-
- oc
- online-casino
-
(und %d Weitere)
Getaggt mit:
-
Hallo Ropro, also ich bitte Dich, so habe ich es wirklich nicht aufgefaßt. Du hättest auch in Riesenlettern "Fehler" schreiben können, und wärest immer noch im Recht gewesen. Ich bin ja dankbar für jede Fehlerkorrektur, besonders für die aus "Betriebsblindheit" entstandenen. Da ich sowieso im Moment bei diesem Thema bin, konnte ich auch die betreffende Datei schnell finden, und das Schaubild ändern. Richtig ist einfach besser als falsch. Also, nochmals danke! Gruß elementaar
- 451 Antworten
-
- oc
- online-casino
-
(und %d Weitere)
Getaggt mit:
-
Hallo Ropro, danke für Deinen Kommentar und Dein aufmerksames Lesen. Leider habe ich, wie mir gerade auffällt, oben irrtümlich Deinen Namen klein geschrieben. Du hast recht, und doch bitte ich, es so lassen zu dürfen, wie es ist. Ich fasse bei den Werten der Abweichung dieses Prozentzeichen als Einheitenkürzel auf. Wer soll das, außer mir, sonst wissen?! Das ist so zweifelsohne nicht korrekt und geeignet, Verwirrung zu stiften. Dafür bitte ich um Entschuldigung. Es ist dem Umstand geschuldet, daß ich die Tabelle nicht speziell für dieses Forum neu erstellt habe und es intern so gewöhnt bin, weil es mir so mehr sagt. Gruß elementaar
- 451 Antworten
-
- oc
- online-casino
-
(und %d Weitere)
Getaggt mit:
-
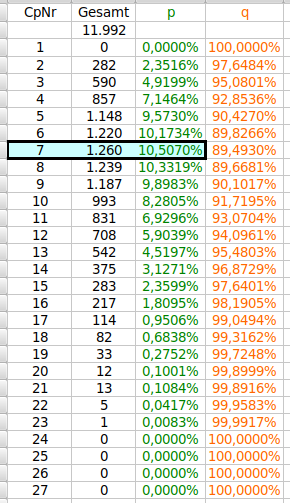
Hallo hemjo, die einfache Standardabweichung errechnet sich aus: Wurzel aus ( [Anzahl der Ereignisse x Trefferwahrscheinlichkeit p = Erwartungswert] x Gegenwahrscheinlichkeit q) Die Werte für p und q kann man sich natürlich aus Ropros Tabelle herleiten. Das sieht dann so aus: Der Nachteil ist, daß durch die Kleinheit der Stichprobe auch die errechneten Werte ungenau werden. Besser sind berechnete Werte (ähnlich wie im 7, 8, 9 Thema) Hier sind sie: Laß Dich durch die Zusatzinformationen in der Tabelle nicht verwirren, uns interessieren hier nur, die mittleren Spalten, Coupnummer (CpNr) und p (in grün; Spalte "Anteil errechnet"). Für Coupnummer 7 lesen wir beispielsweise ab: p= 10,58% oder, bloß anders geschrieben 0,1058. q ist dementsprechend 1 - 10,58% = 89,42% oder 0,8942. Der Erwartungswert für Ropros Stichprobe in Coupnummer 7 ist demnach: 11.992 (Ereignisse) x 0,1058 = 1268,7536 Das bedeutet: wenn wir 11.992 mal nach dem ersten Pleinzweier fragen, sollte dieser rund 1269 mal im siebten Coup erscheinen. Die Standardabweichung errechnet sich daher: Wurzel aus (1268,7536 x 0,8942) = 33,68, gerundet 34. Fertig! Auf 11.992 Ereignisse solltest Du, gerundet, in Coupnummer 7 im 1-sigma-Bereich also zwischen 1269+34= 1303 und 1269-34=1235 Exemplare sehen. Im 3-sigma-Bereich 1269+(3x34)=1371 und 1269-(3x34)=1167. Wie Du siehst sind die natürlichen Schwankungen selbst bei mickrigen +-1 sigma schon 1303-1235=68 Exemplare groß. Das kannst Du jetzt, Coupnummer für Coupnummer, nach diesem Muster weiterrechnen, und, wenn Du willst, in Dein Diagramm einzeichnen. Gruß elementaar
- 451 Antworten
-
- oc
- online-casino
-
(und %d Weitere)
Getaggt mit:
-
Hallo hemjo, das kann man natürlich machen und ist für einen einzelnen Punkt keine große Sache. Nach einer längeren Epistel an ratzfatz bin ich etwas außer Atem und habe jetzt auch keine Zeit mehr. Aber nachher, wenn gewünscht, kann ich Dir etwas einstellen, das zeigt wie es geht. Gruß elementaar
- 451 Antworten
-
- oc
- online-casino
-
(und %d Weitere)
Getaggt mit:
-
7,8,9 besser als 24?
topic antwortete auf elementaar's mamarketing in: Statistik, Abkürzungen, Phänomene, Mathematik
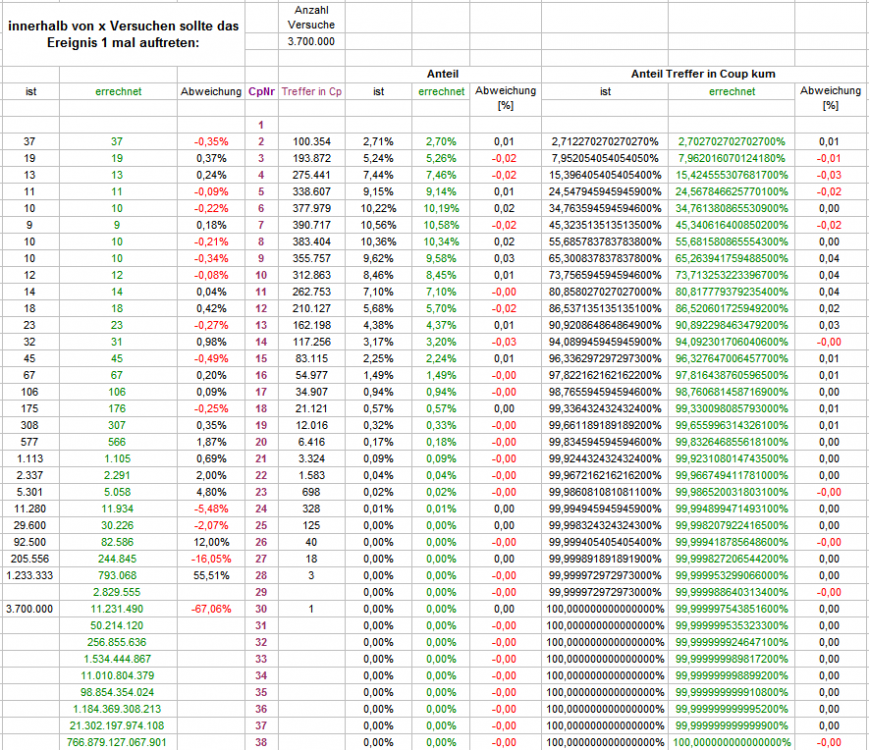
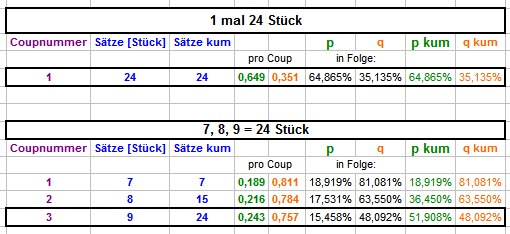
Hallo ratzfatz, ich versuche es einmal so wert- wie ironiefrei wie möglich zu formulieren (keinerlei böse Absicht!): daß jemand hergeht und in der groß mit "Einzelzahl" überschriebenen Tabelle die doppelt bedingte, kumulierte Wahrscheinlichkeit für Coup 7, 8 und 9 abliest, diese Zahlen addiert und tatsächlich meint, damit den richtigen Wert für das Spiel mit zuerst 7 Stücken in EINEM Coup, bei Fehltreffer mit 8 Stücken im nächsten einzelnen Coup, bei wieder Fehltreffer mit 9 Stücken im nächsten einzelnen Coup zu erhalten - ich hätte es nie für möglich gehalten. Und so gesehen, kann ich mir dann jede Arbeit sparen. Dabei zunächst vielen herzlichen Dank vor allem an @Egoist, @Hans Dampf, auch an @roemer! Eure Hartnäckigkeit hat es erst vermocht, ratzfatz seine Summandenrechnung zu entlocken. Aber zurück: die Eigenart der Kettenrechnung ist es doch gerade, daß das Ergebnis aus Zeile 1 erst ermittelt werden muß, um dann zur Weiterverarbeitung in Zeile 2 als Grundlage zu dienen. Irgendwelche Abkürzungen gibt es nicht, sie sind geradezu verboten, und zwar streng! Setze ich im ersten gespielten Coup 7 Zahlen gleichzeitig, ist die Trefferwahrscheinlichkeit p=7/37=0,189 oder anders ausgedrückt 18,9%. Das kann doch gar nicht sinnvoll diskutiert werden, so klar ist das. Schon dies unterscheidet sich deutlich davon, 7 Coups lang jeweils eine Zahl zu spielen mit ihren kumulierten 17,452%. Das könnte einem schon mal einen Fingerzeig geben, daß man sich vielleicht auf dem Holzweg befindet. Weiter: Nach Coup 1 (mit 7 gleichzeitig gespielten Zahlen) haben 18,9% der Fälle ihren Treffer erzielt, sie spielen in dieser Partie hinfort nicht mehr mit. Übrig bleiben jene 81,1% der Fälle, die noch keinen Treffer erzielt haben. Diese, und ausschließlich und nur diese 81,1% der Fälle spielen den nächsten Coup mit 8 Zahlen gleichzeitig. Trefferwahrscheinlichkeit p=8/37=0,216 oder 21,6% (abgebildet in der ERSTEN Tabelle, die betreffenden Spalten überschrieben mit "pro Coup"). 21,6% von was? Na, von jenen 81,1% der Fälle natürlich, die überhaupt noch im Spiel sind und gesetzt haben. Folglich lautet die richtige Rechnung: 81,1% x 21,6% = 17,5%. Nach Coup 2 haben also weitere 17,5% der Fälle ihren Treffer erzielt. Diese spielen in dieser Partie nicht mehr mit, sie haben ja jetzt auch den Treffer erzielt. Es verbleiben 81,1% - 17,5% = 63,6% Lediglich diese 63,6% spielen jetzt noch ein drittes Mal, diesmal mit 9 gleichzeitigen Zahlen. Ihre Trefferwahrscheinlichkeit ist: p=9/37=0,243 oder 24,3%. Wiederum von was? Natürlich ausschließlich von jenen 63,6% der Fälle, die überhaupt noch mitspielen, die anderen sitzen ja schon mit erfolgreichem Partieziel an der Bar. Also: 63,6% x 24,3% = 15,5% So, und jetzt erst, ohne Abkürzung, kann man addieren: aus Coup 1: 18,9% aus Coup 2: 17,5% aus Coup 3: 15,5% Gesamt (kumuliert): 51,9% Wie schön zu sehen, ist es unabdingbar, Zeile für Zeile vorzugehen und die jeweils verbliebene Gegenwahrscheinlichkeit der Trefferwahrscheinlichkeit der aktuellen Chancengröße auszusetzen. Als letztes (jetzt muß heftig gerundet werden): 100 Leute spielen dieses Spiel. 19 Leute treffen im ersten Coup. 81 Leute, obwohl schon mit 7 Stück Verlust aus dem ersten Coup, erhöhen ihre Chancengröße auf 8 gesetzte Zahlen (und damit ihre Trefferwahrscheinlichkeit in diesem Coup von 18,9 auf 21,6%). Und trotzdem dürfen nach dieser Runde nur weitere 18 (nämlich 21,6% von ihnen) an die Bar. Einer weniger als in Coup 1. Die verbleibenden 63 Leute erhöhen nochmals ihre Chancengröße auf 9/37, und dennoch schaffen es nur 15 (Rundungsfehler ausgeglichen) einen Treffer zu erzielen. Ergebnis: 52 Leute zufrieden an der Bar, 48 Leute mit 24 Stück Minussaldo an der Backe, mit 'Pech gehabt', oder 'wie konnte das passieren'. Gruß elementaar -
7,8,9 besser als 24?
topic antwortete auf elementaar's mamarketing in: Statistik, Abkürzungen, Phänomene, Mathematik
Hallo ratzfatz, ganz meinerseits, weil ich nicht verstehe, worin Dein Einwand bestehen könnte. Doch, das habe ich geschrieben. Und Du fragst: Rund 65% zu rund 52% sind nicht dasselbe, wieso sollte ich "meinen", sie seien es? Das tue ich nicht. Um mit dem Spiel pro-Coup-eine-Einzelzahl auf eine kumulierte Erfolgswahrscheinlichkeit von 51,908% zu kommen, muß man zwischen 26 und 27 Coups spielen, wie aus der zweiten Tabelle hervorgeht. Das war aber nicht die Frage von mamarketing. Und es ist auch nicht dasselbe. Mit dem Einzelzahlenspiel über 24 Coup (=24 Stück Maximaleinsatz, wenn man vorher nicht getroffen hat) kommt man auf 48,189% Erfolgswahrscheinlichkeit. Auch das ist eindeutig eine andere Zahl als die beiden anderen. Und das sehe ich auch so. Wieso auch nicht? Du fragst also etwas, was ich gar nicht schreibe, und, sei versichert, auch nicht "meine". Zumal ich aus der Praxis auch weiß, daß die drei Methoden zu unterschiedlichen Erfolgswahrscheinlichkeiten führen. Was soll ich da antworten? Gruß elementaar -
7,8,9 besser als 24?
topic antwortete auf elementaar's mamarketing in: Statistik, Abkürzungen, Phänomene, Mathematik
Hallo ratzfatz, die Frage von mamarketing lautete: "Ist es mathematisch gesehen dasselbe, einmal 7, bei Misserfolg 8, bei erneutem Misserfolg 9 Pleins zu setzen als gleich 1 x 24 Pleins zu setzen? " hier nachzulesen: https://www.roulette-forum.de/topic/18595-789-besser-als-24/?tab=comments#comment-403723 Diese habe ich beantwortet. Ich kann nicht erkennen, daß das nicht die Frage war. Auch hier kann ich nicht erkennen, wo ich in meinem Text etwas geschrieben haben könnte, was die Frage rechtfertigt. Aber klare Antwort: Nein, weder wirklich noch unwirklich sind für mich 64,865%, 51,908% und 48,189% dasselbe. Allein optisch sehen diese Zahlen doch ziemlich verschieden aus, sie bedeuten auch etwas verschiedenes. Gruß elementaar -
7,8,9 besser als 24?
topic antwortete auf elementaar's mamarketing in: Statistik, Abkürzungen, Phänomene, Mathematik
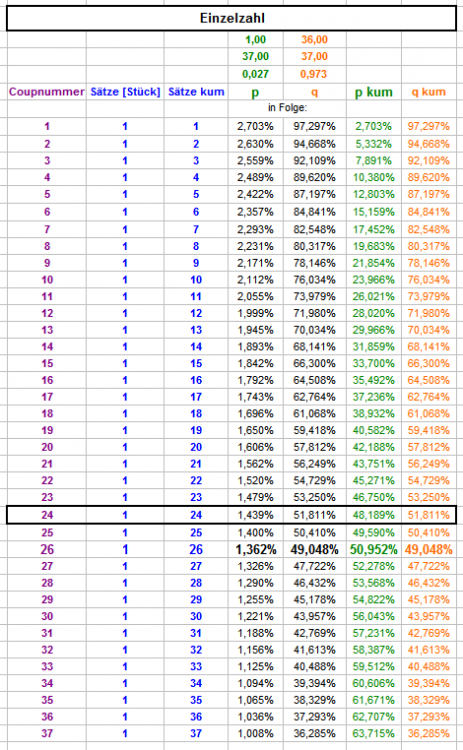
Hallo mamarketing, falls Du noch mit liest, und auf eine korrekte Antwort auf Deine Frage wartest: Und hier für den Fall, daß 24 mal eine einzige Zahl in Folge gespielt wird: Die richtigen Werte müssen natürlich per Kettenrechnung ermittelt werden. Sie stellen sich als Anteilsprozentwerte ein, wenn man unendlich viele Zahlen betrachtet. Als Lesebeispiel die Tabelle mit dem Satz einer Einzelzahl in Folge. Die Wahrscheinlichkeit, eine einzelne Zahl im nächsten Coup zu treffen, ist (bei 37 Möglichkeiten) immer [p=] 1/37 = 0,027 oder 2,703%, die Wahrscheinlichkeit nicht zu treffen (Gegenwahrscheinlichkeit) ist immer [q=] 1 - 1/37 = 0,973 oder 97,297% (im Tabellenkopf zentral vermerkt). In der Zeile mit Coupnummer 1 findest Du genau diese Werte. Nach Coupnummer 1 wurde in 2,703% der Fälle getroffen, in 97,297% der Fälle wurde nicht getroffen. Diese 97,297% der Fälle (und nur diese) spielen in Coupnummer 2 ein weiteres Mal eine einzige Zahl ([p=] 2,703%). Die Wahrscheinlichkeit in diesem zweiten Coup zu treffen ist also 97,297% x 2,703% = 2,630%. Die Wahrscheinlichkeit auch hier nicht zu treffen (Gegenwahrscheinlichkeit) ist mithin 97,297% (aus Coup 1) - 2,630% (aus Coup 2, wie gerade errechnet) = 94,668%. Coup 3 analog: 94,668% (q aus Coup 2) x 2,703% (p für den nächsten Coup) = 2,559% q für Coup 3: 94,668% (aus Coup 2) - 2,559% (aus Coup 3, gerade errechnet) = 92,109%. Und so fort. Die kumulierten Werte findest Du, grün und orange gefärbt, in den Spalten "p kum" und "q kum". In der ersten Tabelle habe ich die Einzelwahrscheinlichkeiten, da sich die Wahrscheinlichkeiten durch unterschiedliche Chancengrößen ändern, in zwei Extraspalten (überschrieben mit "pro Coup") festgehalten. Auf diese Weise kannst Du, auf einfachste Art, die kumulierten Wahrscheinlichkeiten für von Coup zu Coup unterschiedliche Einsätze berechnen. Zusammengefaßt die kumulierten Erfolgswahrscheinlichkeiten: 24 Zahlen in 1 Coup setzen: 64,865% 7, bei NichtTreffer 8, bei NichtTreffer 9 Zahlen in höchstens 3 Coups setzen: 51,908% 1 Zahl in höchstens 24 Coups setzen: 48,189% Gruß elementaar -
Verlust-Zähler in Excel
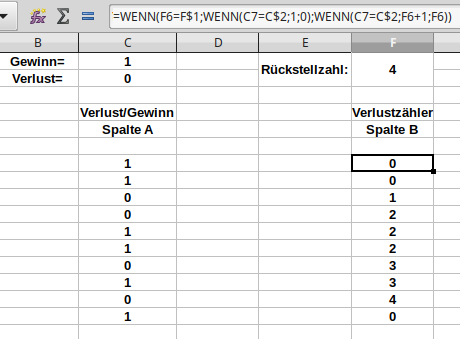
topic antwortete auf elementaar's Leibspeise in: Excel Formeln und Makros, Programmier-Lehrgänge
Hallo Leibspeise, ich gehe davon aus, Du möchtest eine Lösung für "Spalte B". Meine sieht so aus: Mit "Verlust=" in Zelle C1 und "Rückstellzahl" in Zelle F1 wird das Zurückstellen des Zählers dynamisch gemacht, d.h. wenn Du irgend wann den Verlustzähler bei "6" zurück gestellt haben möchtest, trägst Du dies einfach in Zelle F1 ein. Die Zellbezüge natürlich für Deine Umgebung anpassen. Gruss elementaar -
Brauche Hilfe bei VBA
topic antwortete auf elementaar's ecart in: Excel Formeln und Makros, Programmier-Lehrgänge
Hallo ecart, ich verstehe Deine Anfrage so, daß, falls es ein Ergebnis gibt, dieses in eine Extraergebnisspalte eingetragen werden soll. Falls dies so sein sollte, geht mein Beispiel von Spalte "Z11:Z10010" für diese Ergebnisse aus. In Zelle "Z10" wird die Anzahl der schon vorhandenen Ergebnisse gezählt mit (in Zelle "Z10" eintragen): =Anzahl(Z11:Z10010) Das Makro geht dann so: ====== Sub Neues_Ergebnis_eintragen() 'Tabellenblattname von "ecart" zu Deinem Blattnamen ändern! Sheets("ecart").Select Dim VarErg As Object Set VarErg = Range("G10") Dim VarAnzahlErg As Object Set VarAnzahlErg = Range("Z10") If VarErg = "" then goto z else Range("Z11").Select ActiveCell.Range("A1").Offset(VarAnzahlErg, 0).Select ActiveCell = VarErg.Value end if ActiveWorkbook.Save z: End Sub ====== Gruß elementaar -
Erscheinungshäufigkeiten der Pleins innerhalb 37 Coiups
topic antwortete auf elementaar's Sven-DC in: Statistik, Abkürzungen, Phänomene, Mathematik
Hallo Hans Dampf, sehr gut, daß Du den viel weiter oben schon von scoville gebrachten scheinbaren Einwand noch mal hervor holst. Ihm liegt der, meiner Meinung nach, irrige Ansatz zu Grunde, es würde bei der im Raum stehenden Frage irgendeinen Unterschied machen, ob man, auch teilweise, für jeden Cp neue, teilneue oder die alten oder noch ganz andere Zahlen spielt. Begründung: Natürlich ergeben sich unterschiedliche Coupstrecken, wenn man nach Dopplern (soll heißen: unterbrechungsfreie Mehrfachtreffer in aufeinanderfolgenden Cps) von "irgendeinem" im Vergleich zu einem "bestimmten" Dutzend fragt. Das ist klar. Aber was heißt das real für einen Spieler, der darauf abzielt? Der Spieler des "bestimmten" Dutzends kommt nur zum Satz, wenn "sein" Dutzend im Coup zuvor schon einmal erschienen ist. Er macht damit lediglich gut 2/3 weniger Umsatz auf derselben Spielstrecke als ein Spieler, der, des Doppelns wegen, in jedem Coup das zuvor gekommene Dutzend nachsetzt, genau so wie der Spieler, der "irgendein" Dutzend (per Hellseherei, Gefühl, qualifizierten Ratens, weil der Wurfcroupier einen Schnurrbart trägt etc.) in jedem Coup setzt, genauso wie der Spieler, der jeden Coup ein "bestimmtes" Dutzend setzt. Umgekehrt: setzen die aufgezählten jeden-Coup-Spieler nur jeden dritten Coup, machen sie genauso viele Sätze wie der auf-Doppler-eines-bestimmten-Dutzends-Spieler. Und alle erleben haargenau die gleichen Trefferabstände (bezogen auf die gleiche gesetzte Spielstrecke (Sätzeumsatz) und genügend langes Spiel). Es mag banal und provozierend klingen: Für den nächsten Coup muß sich ein Spieler immer auf etwas "bestimmtes" festlegen, sonst kann er nicht am Spiel teilnehmen. Um es noch weiter zu verdeutlichen: Vor einiger Zeit hast Du, im Zuge des BINPOI-Zinnobers, ein Experiment angeregt: https://www.roulette-forum.de/topic/18025-testreihe-sven%C2%B4s-spiel/?page=10&tab=comments#comment-356969 Ich habe das in der Folge auf gleiche Art bis zum ersten 5er weitergeführt (bei Bedarf kann ich die Tabellen einstellen): es zeigten sich keinerlei Auffälligkeiten. Die Ergebnisse zeigen nun zweierlei: 1. natürlich, Favoriten haben auf Dauer, wie sie auch im Einzelfall heißen mögen, keine erhöhte Trefferwahrscheinlichkeit. 2. alle anderen (zusammengenommen) aber auch nicht, denn sonst müßten die Favoriten unterdurchschnittlich gekommen sein. Derselbe Befund bei Restanten, Normalos und was man sich sonst noch ausdenken mag. Ist aber die Trefferwahrscheinlichkeit entsprechend der Chancengröße, sind es die Trefferabstände ebenso, und verhalten sich so, wie sowohl errechnet, als auch experimentell bestätigt. Entscheidend ist das ERGEBNIS des jeweiligen Satzes, nicht wie es zustande kam. Falls es mir nicht gelungen ist, bis hierhin deutlich genug zu schreiben, rege ich noch das Gedankenexperiment aus umgekehrter Warte an: Gäbe es einen (Um-)satzwirksamen Unterschied zwischen "bestimmtem" und "irgendwelchem" Dutzend, müßte dies eine unterschiedliche Trefferwahrscheinlichkeit bedeuten. Schön wär's, begegnet ist sie mir allerdings noch nicht. Gruß elementaar -
Erscheinungshäufigkeiten der Pleins innerhalb 37 Coiups
topic antwortete auf elementaar's Sven-DC in: Statistik, Abkürzungen, Phänomene, Mathematik
Leider steht der beleglose Vorwurf der "Fälschung" und "Manipulation" im Raum. Es erscheint deshalb angezeigt, auf einen großen Vorteil der Wissenschaften noch einmal explizit hinzuweisen: Niemand muß die von mir zwar gewissenhaft, aber vielleicht doch fehlerbehaftet, aufgefundenen Werte "glauben". Jeder ist in der Lage, den weiter oben detailliert beschriebenen Versuchsaufbau für sich zu reproduzieren, und so die mitgeteilten Werte mit eigenem Zufallszahlenmaterial zu überprüfen. Und sollte das, mindestens bei Zweifeln, auch tun. Bei Abweichungen von mehr als den zufallsbedingten Schwankungen, wäre eine Diskussion darüber auch interessant. Ein belegloses "stimmt nicht" ist allerdings nicht akzeptabel, von obigen Worten zu schweigen, die leider eine noch ganz andere Qualität haben. Gruß elementaar -
Erscheinungshäufigkeiten der Pleins innerhalb 37 Coiups
topic antwortete auf elementaar's Sven-DC in: Statistik, Abkürzungen, Phänomene, Mathematik
Nein. -
Erscheinungshäufigkeiten der Pleins innerhalb 37 Coiups
topic antwortete auf elementaar's Sven-DC in: Statistik, Abkürzungen, Phänomene, Mathematik
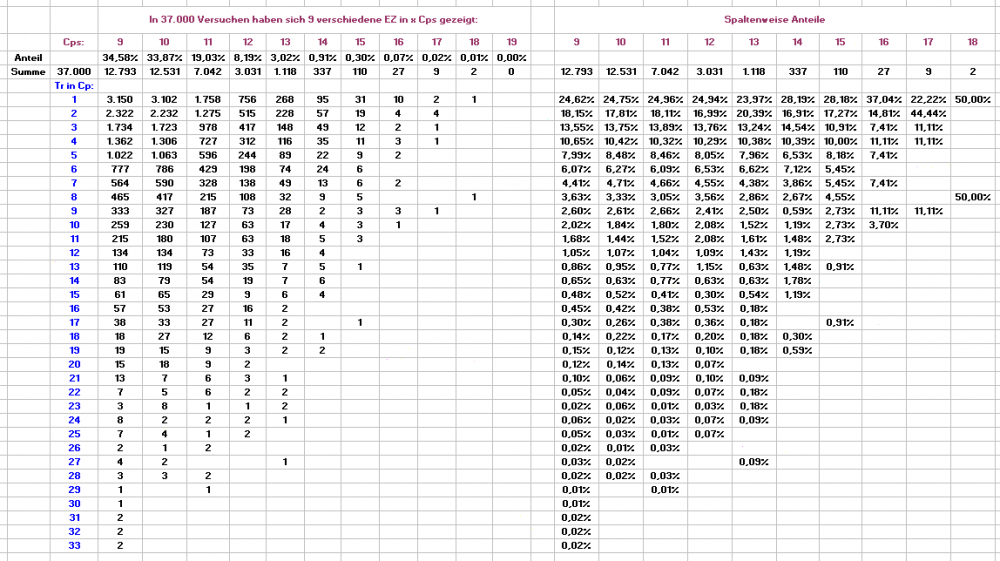
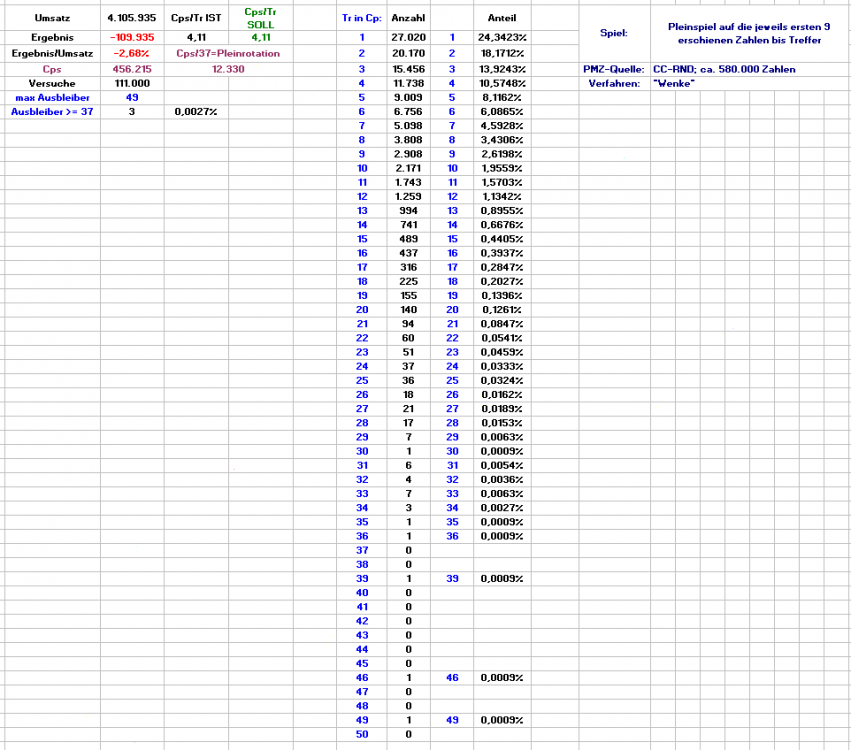
Die Auszählung mit 111.000 Ereignissen (dann ist aber auch Schluß): Das Spiel (wie oben): Es wurde gewartet, bis die ersten neun verschiedenen Zahlen einer Permanenz erschienen sind, danach diese unmittelbar nachgespielt bis zum ersten Treffer. Aufgezeichnet wurden die bis zum Treffer benötigten Coups und als Anzahl in die Wertetabelle eingetragen. Danach Start eines neuen Versuchs mit neuen Permanenzzahlen. Der Versuch wurde 111.000 mal wiederholt. Für 111.000 Treffer wurden 456.215 Coups gebraucht, das entspricht 12.330 (gespielten) Pleinrotationen. Der längsten Ausbleiber waren (unverändert): 49 (Coups bis zum Treffer) (1 mal); 46 (Coups bis zum Treffer) (1 mal); 39 (Coups bis zum Treffer) (1 mal); (siehe Tabelle) Die Anzahl von Ausbleibern >= 37 liegt damit momentan mit 3 (=0,0027%) leicht unterhalb des errechneten Wertes von 0,003322%. Dafür wurden einige Lücken (z.B. 30er Trefferabstand) geschlossen. Das alles nun nicht, um irgendwem auf die Nerven zu gehen, sondern eher als Abfallprodukt, weil ich bei den letzten 37.000 Versuchen noch Zusatzinformationen habe aufschreiben lassen. Es geht um die ersten neun Zahlen (die dann gespielt werden): diese können frühestens in Cp 9 feststehen, je nach Aufkommen von Favoriten aber auch erst deutlich später. Die Frage lautet nun: werden sich Unterschiede in den Trefferabstandsquoten zeigen, je nachdem sich die neun spielbaren Zahlen in neun Cps oder bspw. erst in 14 Cps zeigen? Ich werde die betreffende Tabelle morgen im Laufe des Tages einstellen, bis dahin können Tips, Einschätzungen, Ergebnisse qualifizierten bis vorraussetzungslosen Ratens oder auch Druidenvorhersagen u.ä. hier öffentlich gemacht werden. Preise und Ranglisten soll es aber nicht geben, wer möchte, hat halt Spaß daran. Gruß elementaar -
Erscheinungshäufigkeiten der Pleins innerhalb 37 Coiups
topic antwortete auf elementaar's Sven-DC in: Statistik, Abkürzungen, Phänomene, Mathematik
Hallo Feuerstein, vielen Dank für Dein Lob und Deine erläuternden Worte. So, wie Du es beschreibst, habe ich es bisher auch gesehen. Deshalb Dank für Deine Vermittlung. Vielleicht haben mich aber auch die Worte von Egoist ("Fälschung", "vom Tisch wischen", "von unzutreffender Kritik nicht lassen wollen" sich aufbauende "Wut" etc.) zu sehr beeindruckt. Warten wir einmal ab, ob und wie Egoist seine Sicht der Dinge konkret erläutert. Gruß elementaar -
Erscheinungshäufigkeiten der Pleins innerhalb 37 Coiups
topic antwortete auf elementaar's Sven-DC in: Statistik, Abkürzungen, Phänomene, Mathematik
Hallo Ropro, ich habe per Verfahren "Wenke" für jeden Versuch ein neues Permanenzstück von 497 Cps Länge erstellen lassen (siehe auch rechts oben in den Tabellen). Dies schien mir eine genügend lange Strecke, damit sich sowohl neun verschiedene Zahlen bilden konnten, als auch um danach noch auf einen Treffer kommen zu können. Hätten sich während der Auszählung entweder keine neun verschiedenen Zahlen gezeigt, oder wäre mit diesen kein Treffer zu erzielen gewesen, hätte die Auszählung mit Warnschild gestoppt. Dies war nicht der Fall. Es ging mir dabei um eine möglichst schnelle, dabei aber genügend valide Antwort auf die Frage von Albatros. Ein Rollieren fester Permanenzstränge hätte eine unvergleichlich höhere Anzahl an Versuchen erfordert, bis die Schwankungen sich einigermaßen beruhigt hätten. Mit Cp-zu-Cp-Verlaufsdaten kann ich also leider nicht dienen. Gruß elementaar -
Erscheinungshäufigkeiten der Pleins innerhalb 37 Coiups
topic antwortete auf elementaar's Sven-DC in: Statistik, Abkürzungen, Phänomene, Mathematik
Hallo Feuerstein, Das ist gut möglich, deshalb vielen Dank für Deinen Versuch der Übersetzungshilfe. Man kann ja über vielerlei anderer Ansicht sein, kein Problem, ich wüßte halt nur gern, worüber wir denn angeblich anderer Ansicht sind. Ich vermag das nicht zu erkennen. Vielleicht ist meine Versuchsbeschreibung nicht eindeutig genug gewesen. Folgendes habe ich bei der Auszählung gemacht: Zuerst wurde gewartet, bis sich in der, für jeden Versuch jeweils neu erstellten, Permanenz neun unterschiedliche Zahlen gezeigt haben (= nicht mitgezählter Vorlauf unterschiedlicher Länge). Sobald diese neun Zahlen ermittelt waren, wurden eben diese bis zum ersten Treffer gespielt und die zum Treffer benötigten Satzcoups aufgezeichnet. Also zum Beispiel: In neun (nicht mitgezählten) Coups erscheinen neun verschiedenene Zahlen ==> 1. Satz in Cp 10 (zählt als Satz 1), wenn Treffer ==> Verzeichnet in Tabelle unter "1" +1mal, neue Permanenz; wenn NichtTreffer ==> 2. Satz in Cp 11 (zählt als 2. Satz), wenn Treffer ==> Verzeichnet in Tabelle unter "2" +1mal, neue Permanenz; wenn NichtTreffer ==> 3. Satz in Cp 12 (zählt als 3. Satz) usf. Es wurde immer bis zum ersten Treffer gespielt (also auch über eine "Rotation" hinaus, siehe Trefferabstände > 37), die jeweilige Spieldauer bis zum Treffer als Anzahl (in den Spalten) notiert, und, zusätzlich, die verbrauchten Cps summiert. In der letzten Tabelle https://www.roulette-forum.de/topic/18009-erscheinungshäufigkeiten-der-pleins-innerhalb-37-coiups/?page=2&tab=comments#comment-386800 kann man also in den mittleren Spalten ablesen: (blau gefärbt und mit "Tr in Cp" überschrieben, von oben nach unten zu lesen:) die Trefferabstände 1 -50. Daneben (mit "Anzahl" überschrieben): Die in 74.000 Versuchen aufgefundenen Anzahlen der Trefferabstände. Also bspw. in "Tr in Cp" "10" "1.467" Exemplare mit dieser Spielstrecke, was bedeutet es wurden 10 x 1.467 = 14.670 Cps verbraucht, um diesen Trefferabstand in dieser Anzahl während der gemachten 74.000 Versuche zu erzielen. Links oben in der Tabelle (in Schriftfarbe coral, neben "Cps") ist die Summe aller verbrauchten Cps genannt ("304.540"). Dieselbe Zahl muß sich ergeben, wenn man (mittlere Spalten) rechnet: (17.847 x 1 Cp) + (13.514 x 2 Cps) + (10.392 x 3 Cps) + (7.865 x 4 Cps) + usf. Diese Zahl "304.540" der tatsächlich gespielten Cps für 74.000 erfolgreiche Trefferversuche teile ich unter "Cps/37=Pleinrotation" ,wie damit definiert und genau beschrieben, durch 37 und komme auf 8.231 Pleinrotationen. Weder zähle ich die (Cps-)Zeit bis zum Enstehen der neun überhaupt erst spielbaren Zahlen mit, noch irgendetwas, was erst nachdem der Treffer gekommen ist passiert: warum auch, das war nicht die Frage von @Albatros. Daß nach bspw. Treffer im ersten Satz (-Coup) ein neues Spiel beginnt, ist klar und eindeutig beschrieben. Daß damit die "Rotation" "abgebrochen" würde, ist ja ein Verständnisunsinn, den ich Egoist gar nicht zutraue. Als würde es irgendeinen Unterschied machen, ob ich nach Treffer neue neun Zahlen ermittele, oder mit den alten bis in alle Ewigkeit weitermache. Welche "abgebrochene" "Rotation" denn? Was nach dem Treffer passiert, interessiert doch niemanden, und ist für die in Frage stehende Frage auch ganz unerheblich. Sollte Egoist tatsächlich eine Methodenkritik beabsichtigt haben, bin ich auf seine diesbezügliche Argumentation aber mal sehr gespannt. Also vielen Dank, Feuerstein, für Deinen Übersetzungsversuch, aber wie Du siehst, so wirklich weiß ich immer noch nicht, was Egoistens Wut entfacht hat, und wie man da Abhilfe schaffen könnte. Gruß elementaar PS: Mir fällt gerade noch ein: Vielleicht nährt sich Egoistens Wut aus meiner Umbennung seiner 30.103 "Rotationen" in "Versuche". Also: Er nimmt sich 30.103 mal Permanenzstücke von je 37 Cps Länge, und wird dann, im Schnitt, 1 mal keinen Treffer in einem 37-Cps-Stück erblicken. Das ist aber doch ganz unbestritten, wenn auch praxisirrelevant und nicht die Frage von Albatros. Denn man kann daraus nicht einfach die real gespielte Strecke machen, da 1. müßten dann auch die Mehrfachtreffer innerhalb der 37er-Stücke gezählt werden, und 2. hätten wir dann das Problem der NichtTreffer-Überlappung am Ende bzw. Anfang eines jeden Teilstücks. Würde man das, viel komplizierter, korrekt machen, kämen aber dennoch keine anderen Verhältnisse heraus, als in meiner Tabelle abgebildet: nämlich auf 17.847 Treffer im ersten Satzcoup, kommen knapp drei Treffer, die länger als 37 Cps auf sich warten lassen.