elementaar
Mitglieder-
Gesamte Inhalte
1.145 -
Benutzer seit
-
Letzter Besuch
elementaar's Achievements
Mentor (12/14)
-
-
Rare
-
-
-
Rare
Recent Badges
-
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Wenn ich mich recht erinnere, fand die RNF und GUT Entwicklung im anderen, verblichenen Forum statt. Extrakte daraus (und ein unschöner Streit über "Multinomialverteilung") im englischsprachigen (ich glaube vls) Forum. Da auch die sehr schön gemachte (aber vollständig, soll man sagen "geklaute"?) Broschüre. Beim Eingeben seines Namens hat die Listenfunktion der Forensoftware seine Anmeldung offenbart. Wie es ihm geht und was aus ihm geworden ist, weiß ich leider nicht. Ein heller Kopf jedenfalls. Gruss elementaar -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Das ist mir überwiegend entgangen. Was ER, und vor allem mit welcher "Begründung" ER setzt, langweilt mich so sehr, daß ich schon letztes Jahr beim "Turnier" in dieser Frage abgeschaltet habe. Wie ER auf den Verlauf SEINER Ergebnispermanenz reagiert, ist indiskutabel. Da fehlt es an allem: Grundlagen, Einsicht, Training - nichts. Deutlich faszinierender finde ich SEINE Satzhöhenkapriolen - das nicht kapitalgedeckte hundertfache des Anfangssatzes hatten wir ja schon - der Sinn der ganzen Veranstaltung ist mir allerdings in der vorgetragenen Form sowieso vollkommen unklar, aber ich muss den Sinn ja auch nicht erfassen.. Ja stimmt. Mir fällt noch @Serienkiller als wichtiger Mitstreiter ein, der etliche Auswertungen übernommen hat. Ich sage es gerne und immer wieder: Eine echte Sternstunde (die sich ja auf ein paar Jahre ausgedehnt hat) an öffentlicher Zusammenarbeit zur Untersuchung und Verdeutlichung des Themas (inklusive Neben- und Irrwege, wie könnte es anders sein, aber auch diese gut dokumentiert). Gäbe es eine Ruhmeshalle des Roulettespiels, müsste die damalige Truppe einen prominenten Ehrenplatz einnehmen. Bedauerlich finde ich lediglich, daß die Ergebnisse scheinbar nicht für jeden engagierten Roulettespieler als unverzichtbares Grundlagenwissen auf dem Lehrplan stehen, und statt dessen ein unqualifizierter Scharlatan sein Unwesen treibt. So ist halt auch der Roulettetiergarten groß. Gruss elementaar -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
So ist es. Und erfreulicherweise war damals von dem Fremdfederfisch noch weit und breit nichts zu sehen. -
Wie viele verschiedene Zahlen erscheinen in 30 Coups?
topic antwortete auf elementaar's elementaar in: Höhere Chancen
Einschub 2: Zwei Verdeutlichungen Erstens: Jedem verständigen Leser ist es sowieso klar, dennoch möchte ich betonen: bloß weil in den Tabellen absolute Zahlen und deren Anteilsprozente abgebildet sind und diese zu allerlei Spekulationen verführen, heißt das nicht, daß sie irgendetwas anderes als Tatsachenbeschreibungen sind. Diese Tatsachen entstehen, weil im nächsten Coup p=1/37 gewährleistet ist, und im übernächsten Coup, und im überübernächsten usf. Jeder Versuch, sich aus den abgebildeten Zahlen einen Vorteil errechnen zu wollen, ist vergeblich und Zeitverschwendung. Es geht darum, Aspekte des Permanenzverlaufs deutlicher sichtbar zu machen. Zweitens: Die Möglichkeit, die Ergebnisse der detaillierten "F>1" Auszählung mit der Anzahl der vorgefundenen verschiedenen Zahlen in 30 Coups zu verknüpfen, um so ein noch feineres Abbild des Permanenzverlaufs zu gewinnen, habe ich verworfen. Dank der kombinatorischen Eigenschaft des Roulettespiels wissen wir, daß jede Zahlenkonstellation auf 30 Coups gleichwahrscheinlich mit allen anderen möglichen ist. Verfeinert man seine Betrachtung nun so weit, daß sie in die Nähe bloß einer möglichen Kombination rückt, wird der Aufwand gigantisch und bringt als Ergebnis lediglich und voraussehbar die pure Vernebelung: im nächsten Coup erscheint gleichwahrscheinlich eine von 37 Zahlen. Das kann man aber viel einfacher verifizieren und ist Voraussetzung des Spiels. Wahrscheinlich ist etwas Erfahrung im Umgang mit Zufallsgeschehen nötig, um die nicht sinnvoll überschreitbare Genauigkeitsgrenze zu erahnen. Gruss elementaar -
Wie viele verschiedene Zahlen erscheinen in 30 Coups?
topic antwortete auf elementaar's elementaar in: Höhere Chancen
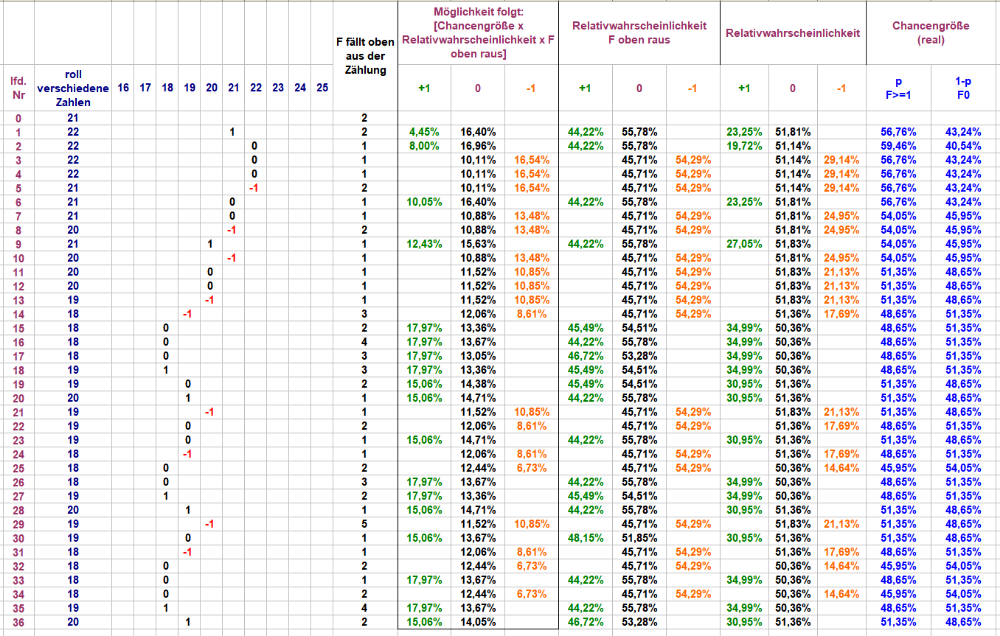
Der oben abgebildete "Beispielverlauf über 36 chronologische Coups" kann also mit neuen Informationen erweitert werden: Wenn man nun unbedingt möchte, hat man die Möglichkeit eines sehr einfachen Spiels (und virtuell seines Gegenteils): -
Wie viele verschiedene Zahlen erscheinen in 30 Coups?
topic antwortete auf elementaar's elementaar in: Höhere Chancen
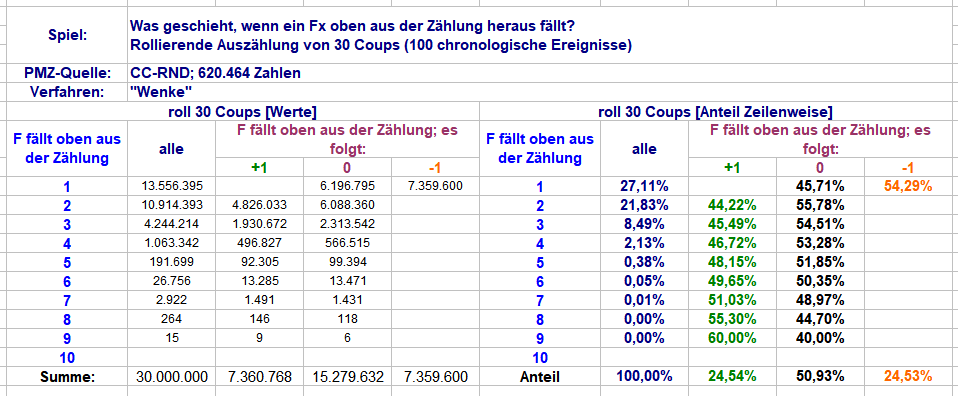
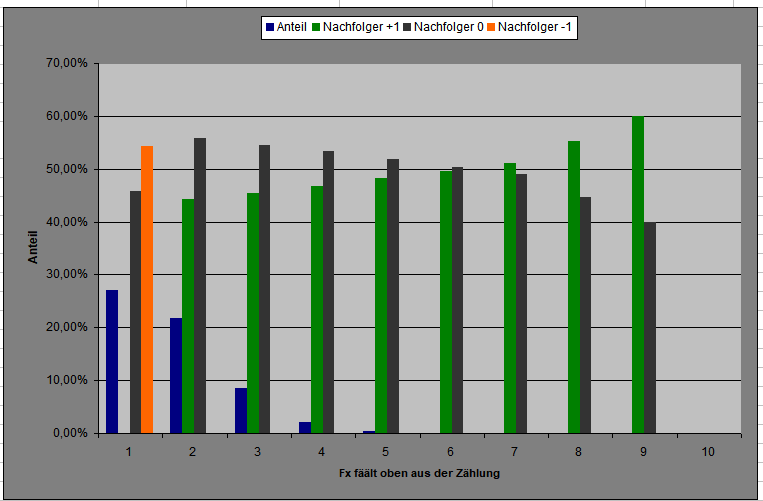
Betrachtet man den oben abgebildeten "Beispielverlauf über 36 chronologische Coups", Spalte "F fällt oben aus der Zählung", so bestimmt die Unterscheidung "F1" und "F>1" die realen Satzmöglichkeiten. Es stellt sich die Frage, ob eine Unterscheidung der zusammengefassten "F>1" in reale "F2", "F3", "F4" etc. einen Zugewinn in der Betrachtung zeigt. Wie zu sehen, gibt es da sehr wohl Unterschiede, ob oben ein "F2", ein "F5" oder ein "F9" (als höchstem, in dieser Stichprobe gezähltem "F") aus der Zählung herausfällt. Erkennbar ist eine abfallende Neigung zur Zahlenanzahländerung "0", je höher die herausfallenden Fx, einhergehend mit einer Steigerung des Anteils von "+1". (Natürlich müssten mindesten F7, 8, 9 wegen zu geringer Anzahl an gezählten Exemplaren noch gesondert verifiziert werden.) -
Wie viele verschiedene Zahlen erscheinen in 30 Coups?
topic antwortete auf elementaar's elementaar in: Höhere Chancen
Hallo @Feuerstein, vielen Dank für den engagierten Enthusiasmus Deiner ersten Reaktion. Daß die Darstellung von (für mich) Altbekanntem diese Wirkung entfalten könnte, hat mich doch erstaunt - und sehr gefreut. Und zerstreute, in diesem Fall, wirksam die Selbstzweifel, ob es den Aufwand überhaupt wert sei, die Tatsachenergebnisse präsentabel zu machen. Herzlichen Dank! Sehr richtig. Was an sich kein Makel sein muss. Da ich mich damit aber so gar nicht wohl fühle, begann ich damals nach Möglichkeiten Ausschau zu halten, mit denen man die Anzahl der zu setzenden Pleins wirksam reduzieren könnte. Aber das ist eine andere Geschichte. Gruss elementaar -
7,8,9 besser als 24?
topic antwortete auf elementaar's mamarketing in: Statistik, Abkürzungen, Phänomene, Mathematik
Schade! Aber bei den derzeitigen Temperaturen kann man seine Zeit ja auch einem schönen, kühlen Getränk widmen. Auf Deine gute Gesundheit! elementaar -
7,8,9 besser als 24?
topic antwortete auf elementaar's mamarketing in: Statistik, Abkürzungen, Phänomene, Mathematik
Bei weitergehendem Interesse vielleicht lohnenswerte Lektüre: Die Hans Dampf und Charly Setzweise -
7,8,9 besser als 24?
topic antwortete auf elementaar's mamarketing in: Statistik, Abkürzungen, Phänomene, Mathematik
Schreibfehlerkorrektur: statt "erläuterten" muss es natürlich "erläuternden" Beispiel heißen. Bei einem Beitrag mit vielen Zitaten scheint die Forensoftware beim "Bearbeiten" überfordert. -
7,8,9 besser als 24?
topic antwortete auf elementaar's mamarketing in: Statistik, Abkürzungen, Phänomene, Mathematik
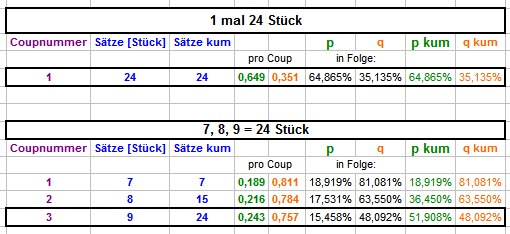
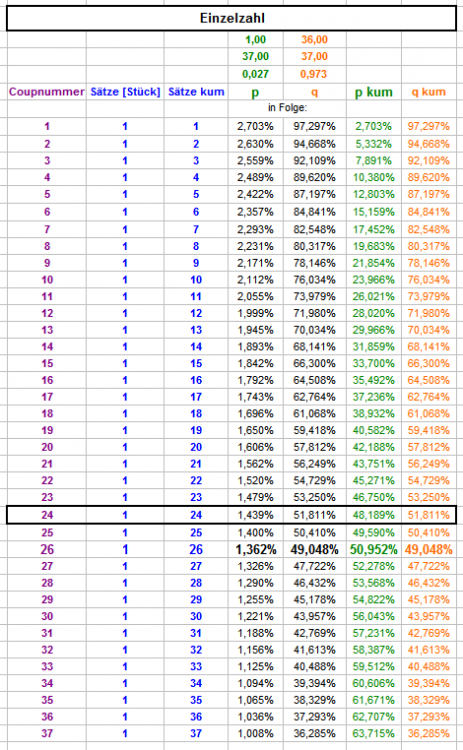
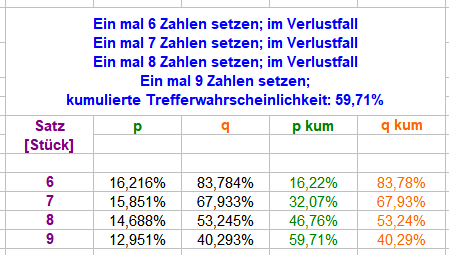
Das ist zweifellos eine wahre Feststellung. Und einige Antwortgeber glaubten auch, die Fragestellung von @mamarketing uminterpretieren zu müssen. Auch diese Aufforderung ist immer höchst empfehlenswert. In diesem Fall ist die Fragestellung jedoch so eindeutig, wie man sie sich eindeutiger nicht wünschen könnte. Nach Themeneröffnung durch ihn selbst, schreibt @mamarketing: U.a. ich beantworte ihm seine Frage vollständig und richtig mit: nebst überausführlicher Erläuterung des Vorgehens und seiner Begründung. https://www.roulette-forum.de/topic/18595-789-besser-als-24/page/2/#comment-403793 Hiermit Hammer! Vielen Dank für diese Darstellung. bedankt sich @mamarketing und damit ist seine Frage zur Zufriedenheit des Fragestellers (und darauf kommt es an) beantwortet. In der Folge und auch der Zwischenzeit demonstriert @ratzfatz die Holzwege, die sich durch ein allzu hemdsärmeliges Vorgehen ergeben können; da ist die eigentliche Frage jedoch längst richtig beantwortet. Aus einem erläuterten Beispiel, scheinst Du nun ein "oder" konstruieren zu wollen (ich hoffe, daß ich mich irre): Für die Erscheinenswahrscheinlichkeiten sind jedoch allein die bespielten Chancengrößen entscheidend, nicht der Zeitpunkt, zu dem sie gespielt werden, und auch nicht die Namen ihrer Mitglieder. Ob jemand 8, 9, 10 Coups ohne Plein-Zweier abwartet und dann die gefallenen Zahlen nachspielt, oder in Coup 1 irgendwelche 7 Zahlen, im Verlustfall in Coup 2 (auch vollständig andere) 8 Zahlen und im Verlustfall in Coup 3 (auch vollständig andere) 9 Zahlen spielt, ist für die Erscheinenswahrscheinlichkeiten vollkommen irrelevant. Sie bleiben immer gleich. Es ist halt ein Kreuz mit nicht verstandenen Verteilungshistogrammen: sie entstehen "weil", nicht "trotz". Gruss elementaar -
Hier bitte: Gewiss. Totaaal logisch. Ganz bestimmt. Drei = Vier. Da habe dann ich keinen weiteren Diskussionsbedarf. Logisch, nicht wahr?
-
Kettenrechnung (Link, mit Maus draufklicken, lesen, verstehen --> lernen.)
-
Drei Fünftel sind gleich so ca. vier Fünftel - also eigentlich nichts Neues vom "math. " Konnte gerade nicht widerstehen, sonst versuche ich mich weiter an zu halten, auch bei Leseschmerzen. Gruss elementaar
-