elementaar
Mitglieder-
Gesamte Inhalte
1.447 -
Benutzer seit
-
Letzter Besuch
Inhaltstyp
Profile
Forum
Kalender
Articles
Alle erstellten Inhalte von elementaar
-
https://www.roulette-forum.de/topic/31209-berechnungbetrachtung-von-soziablen-und-solitären-serien/#comment-519891
-
!!! Tja, das mache ER dann mal mit SICH aus.
-
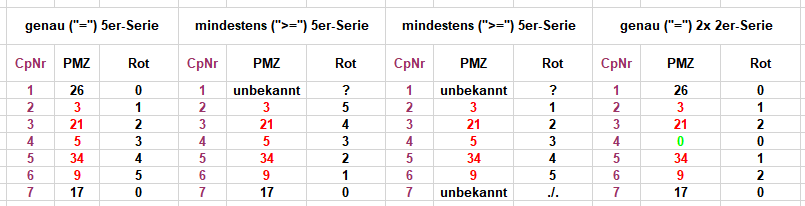
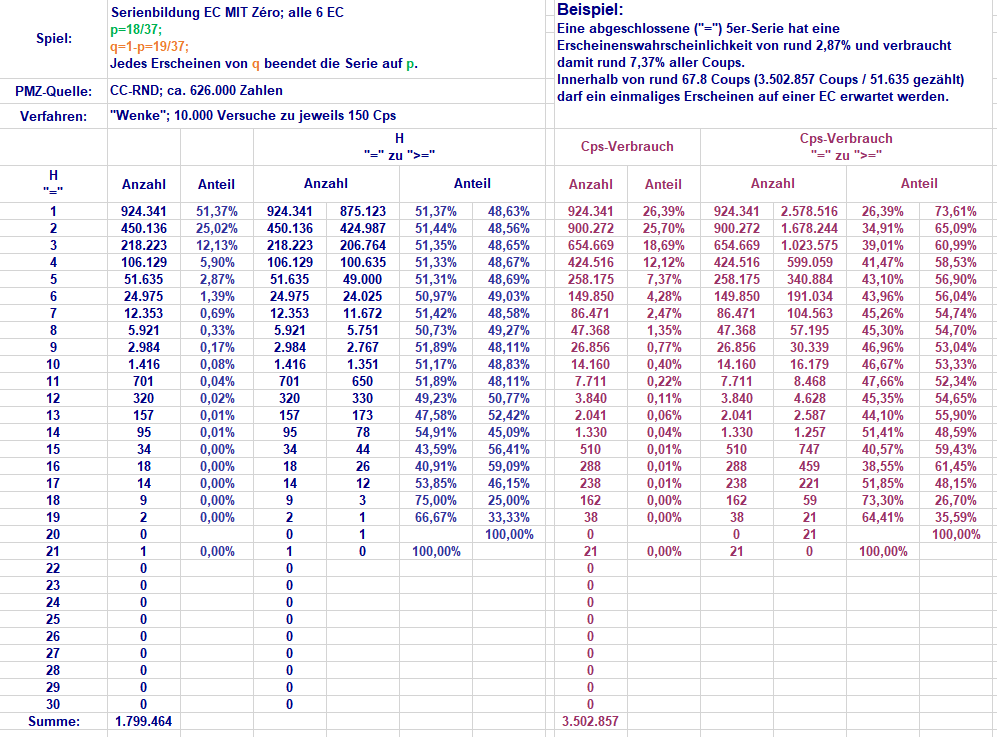
Meine Güte, diese Dreckschleuder hört wohl nie auf. War aber sowieso klar. Schon SEINE pseudointeressierte Nachfrage: machte ja überdeutlich, daß ER diesen Beitrag https://www.roulette-forum.de/topic/31146-lukasz-resurrection/page/11/#comment-528336 in SEINER bornierten Dummheit nicht begreifen konnte. SEIN Urteil dennoch, selbstverständlich: So, dann noch einmal speziell für den offenbar minderbemittelten GröRaZ, der SICH doch ständig mit SEINEM falsch verwendetem solitärsoziabel Gewäsch aufplustert: Es gibt Serien mit genau feststellbarer Länge (=) und es gibt Serien mit Mindestlänge (>=). Beispiel 1 (genau 5er-Serie) und Beispiel 4 (genau 2 mal 2er-Serie) Beispiel 2 und Beispiel 3 zeigen in Mindestlänge 5er-Serien, deren genaue Länge nicht feststellbar ist. In Beispiel 2 ist lfde Nr 1 unbekannt (weil der Tisch gerade erst aufgemacht hat) In Beispiel 3 ist lfde Nr 1 unbekannt (weil der Tisch gerade erst aufgemacht hat) und der nächste Coup noch nicht gefallen ist. Und bevor der nächste Coup gefallen ist, der möglicherweise eine Serie beendet, kann niemals und von niemandem die genaue Serienlänge bestimmt werden; sie ist buchstäblich unbekannt. Ein Kleinkind kann das begreifen, nur ER muss darüber "diskutieren" und sich so weiter disqualifizieren. Wenn das sein soll, dann haben es alle Anderen eben bisher falsch gemacht - was ja gar nicht stimmt. Also hat ER mir mal wieder, diesmal 20 Minuten, meiner Lebenszeit vollkommen sinnloserweise geklaut. Da kann ER jetzt wirklich stolz auf SICH sein.
-
-
-
Und nach wie vor schwadroniert ER wahrheitswidrig von "obwohl", wo es richtig "weil" heißen muss. Das geht über SEINEN armseligen Horizont. Mehr muss man im Grunde über SEIN analphabetisches "Verständnis" von Zufallsgeschehen nicht wissen. Aber ja. Spiel auf Zeit - der Begriff ist in den letzten zehn Jahren ab und zu mal gefallen. Gruss elementaar
-
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Ah ja. Dreister Lügner. Vor 1 (einer!) Stunde schrieb ER: -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Vielen Dank. Ist scheinbar so ein Prophetending mit Wasser und Wein. Immer ganz besonders lustig, wenn ER sich zu Fragen von Anstand und Manieren äußert - ausschließlich bei Anderen selbstverständlich. Schönes Wochende! elementaar -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
https://www.roulette-forum.de/topic/31153-favoritenangriff-nach-bin-öffentliches-testspiel/page/218/#comment-527428 https://www.roulette-forum.de/topic/31153-favoritenangriff-nach-bin-öffentliches-testspiel/page/191/#comment-526318 https://www.roulette-forum.de/topic/31153-favoritenangriff-nach-bin-öffentliches-testspiel/page/143/#comment-523816 https://www.roulette-forum.de/topic/31153-favoritenangriff-nach-bin-öffentliches-testspiel/page/134/#comment-522586 https://www.roulette-forum.de/topic/31234-maßgeschneiderte-rückoptimierte-marschstrategie/page/4/#comment-523707 https://www.roulette-forum.de/topic/31232-nebendiskussion-favoritenangriff-nach-bin-öffentliches-testspiel/page/7/#comment-522700 https://www.roulette-forum.de/topic/31153-favoritenangriff-nach-bin-öffentliches-testspiel/page/117/#comment-521491 Unvollständige kleine Auswahl (!) der letzten Monate. Eine Benennung der Tatsachen ist keine Unterstellung sondern eine Tatsachenfeststellung. -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Mir war die Möglichkeit, es könnte nicht so sein, noch gar nicht bewußt. Danke der Nachfrage! Doch urteile selbst: Quellen: https://shop.segafredo.de/intermezzo-1000-g https://www.matildevicenzi.com/de/product/cantuccini-mit-mandeln-225-g/ https://www.nzz.ch/deutschland Obwohl nun in der Eigen-Lobpreisung vom "12-Zylinder unter den italienischen Espressi!" die Rede ist, scheint mir, auch bei streng angewandten Kriterien, eine Jugendgefährdung sehr unwahrscheinlich. Ist aber natürlich bloß meine Meinung. Zeitlich immer noch sehr eingeschränkt, ist mir dennoch ein Phänomen nicht entgangen, nämlich das vermehrte Auftreten von Geschlechtswandlern. Im Zuge der Saldoverwirrnis wurde aus dem (?) geschätzten @Wenke eine, sozusagen, Wenkin , @D a n n y mutierte zum, wie sagt man das jugendfrei?, Penisbesitzer - und erst gestern wurde: @Hans Dampf (von) per Doppelkomma feminisiert. Klar, wirklich Wissen kann man es bei Aliasnamen per se nicht, eine erkleckliche Anzahl an Leuten ist ja auch nicht mehr in der Lage, den Unterschied von Genus und Sexus zu begreifen, und im Kontext ist es ja auch nicht wichtig - aber mich irritiert es doch. Ist schon schwierig genug, beim Metamorph, also jetzt im übertragenen Sinn, am Ball zu bleiben. Grüsse, bitte auch mit Dank an die Göttin der Morgenröte unter den Titanen! elementaar -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Also, hier muss doch wohl ein Mißverständnis vorliegen! Da haut die intelligenteste, höflichste, immer streng sachgerecht argumentierende, die überhaupt Grösste Ruhlättcornifähre Aller Zeiten (GröRaZ) mal so nebenbei die Quintessenz dessen 'raus, was ER zu Zufallsgeschehen, Rechnen und Logik beizutragen hat - SEIN Lebenswerk sozusagen, noch dazu mit 99% Gewinngarantie (wenn nicht die Schwankungen wären), und wird schon wieder, so scheint's, total verkannt. Dabei meint ER's nur gut: die Fackel der Erleuchtung soll halt auch uns niederen Erdenwurmlingen leuchten. Quelle: https://www.markolorenz.com/die-hoechsten-stufen-der-erleuchtung/ Für SEINE zahllosen Bewunderer noch einmal SEINEN Ursprungsbeitrag (Original Grammatik wie Rechtschreibung, buchstäblich kein Buchstäblein geändert) (Hinweis: Herunterladen und in Fettdruck auf A0 ausdrucken und über's Bett hängen; das kommt so schnell nicht wieder!): Interessant, daß sich der, ganz ähnlich IHM, so überaus, aber eher speziell immer höfliche Krawallbruder @Mark Wendor, oder, am anderen Ende, auch @Schneckchen (Hauptsache: friedlich, egal welcher Schwachsinn, egal wie aggressiv verbreitet wird) gar nicht äußern. Noch ein Hinweis an SEINE Bewunderer: ausschließlich und nur nach 10 x Rot darf man Schwarz setzen, um die 99% zu kassieren, nach 10 x Schwarz ist das was anderes; und bei den anderen 1022, gleichwahrscheinlichen Kombinationen auf 10 Coups, ist es noch mal was ganz, ganz, GANZ anderes. Logisch: ist ja auch nicht 10 x Rot - so lautet nun mal die Kausalkette. Und ER selbst spielt lieber SEIN Mülleimerspiel, weil ER nicht auf 10 x Rot warten will, trotz weit über 99% - da kann man sowieso viel besser falsch rechnen, sich selbst widersprechende Logik hervorblubbern, und von einer Ordnung im Chaos schwadronieren, die sich nach den von IHM persönlich, zu unser aller (aller! paar 2tausend) Wohl, erfundenen Gesetzen richtet. Lieber ein Stück mehr auf dem Solitärpleinzwilling verlieren - da weiß man, was man (dann nicht mehr) hat. Quelle: https://jamesbond.fandom.com/de/wiki/Solitaire Also: Forum schließen, alle ab ins Landcasino und auf Dauer (solange muß Haus und Hof schon reichen) gewinnen weit über 99 von 100 Spielern auf Schwarz nach 10 x Rot. "Schön, dann wäre das ja geklärt." -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Die vereinten KI-Maschinen haben also in Kurz- und Prägnant-Form die mathematische Standardfolklore dargestellt. Vielleicht ist das sogar ab und zu angemessen und kaum jemand mit einem Rest an funktionsfähigem logischen Denkens wird dem widersprechen. Diese mathematische Standardfolklore ist, wie so oft in der Mathematik, sowohl unbestreitbar wahr, wie weitgehend nutzlos. Sie ist für den einzelnen Spieler ein eindringlich warnendes Hintergrundrauschen, bietet jedoch für die Satzentscheidung für den nächsten Coup praktisch keine Hilfestellung - wie denn auch. Für ihn ist es schlichtweg irrelevant, daß er "auf Dauer" keine Chance hat; hat er auf "Rot" gesetzt und es erscheint "Rot", hat er seinen Einsatz verdoppelt. Er hat tatsächlich gewonnen; ihn kümmert nicht, daß jeder Satz (ob mit Gewinn oder Verlust) mit 1/74 dem Hausvorteil unterliegt; ihn kümmert auch nicht, daß, wenn er danach noch 1.000, 10.000 oder 100.000 mal auf "Rot" setzt, es immer unwahrscheinlicher wird, daß er sich der Wahrheit der Großen Zahl erfolgreich entziehen kann. Verzeihung für das Selbstzitat: Selbstverständlich ist es unter den Bedingungen der Großen Zahl vollkommen gleichgültig, was ein Spieler bei Saldostand -2 macht, er wird seinem Schicksal nicht entgehen. Nach zwei gespielten Coups hat er es aber nicht mit der "Großen Zahl", sondern mit der ganz konkreten, geldbeutelwirksam gewordenen Situation zu tun, 2 Stücke im Brand zu sein, und die Möglichkeit mit den nächsten 3 Coups bei Saldo +1 zu landen exakt genauso wahrscheinlich ist, wie weitere 3 Stücke zu verlieren (1/8). Und das ist (für ihn und jeden Anderen in dieser Situation) etwas ganz anderes, als zu Beginn des Spiels: an den Wahrscheinlichkeiten hat sich überhaupt nichts geändert (1/2 für den nächsten Coup, 1/8 für die nächsten drei Coups) - die Treffertatsachen (aus der 2-Coups-Vergangenheit) sind aber andere. Zur weiteren Verdeutlichung richte man sich, spaßeshalber, Folgendes ein: Gleichsatzspiel auf EC (ohne Zéro); zur laufenden Permanenz 101 unabhängige Scheinspieler; die Mehrheit entscheidet, was im nächsten Coup gesetzt wird. Aufgezeichnet wird dabei nicht nur, Coup für Coup, das Ergebnis (+ oder -; Saldo) sondern auch, wie die Mehrheitsverhältnisse sind, die im Coup zuvor zur Satzentscheidung geführt haben. Eine graphische Darstellung der Verläufe ist angebracht. Das macht man so lange, bis der Groschen fällt. Wem das die Augen noch nicht genügend öffnet, kann den selben Versuch auch mit 1.001 Scheinspielern machen. Gruss elementaar PS: Der Beitrag hat sich mit dem von @Chemin de fer überschnitten - beide gehen in dieselbe Richtung. -
Da bist Du mir weit voraus... ich ahnte es schon. In dem Club habe ich auch eine lebenslange Mitgliedschaft. Wenigstens auf Etwas kann man sich verlassen.
- 5.148 Antworten
-
- ec
- intermittenz
-
(und %d Weitere)
Getaggt mit:
-
Hallo @Hans Dampf (von), Wahrscheinlich nichts Neues für Dich: selbst bei den beiden Beispielen von @Feuerstein ist eine situative Spielerentscheidung nötig, nämlich ob 1 x auf Wiederholung (bei Nase: nach links 1 x auf rechts) oder Durchspielen angesagt ist. Im Falle von Serienketten bedeutet das Durchspielen, daß 2er-Ketten nur Umsatz aber keinen Gewinn bringen (immerhin mit der Möglichkeit, bei +1 auszusteigen; mit dem finalen Minusstück bei Abbruch), bei Nasen auch so (mit finalen zwei Minusstücken bei Abbruch). Und 2er-Serien sind nun mal die häufigsten Serienerscheinungen (mit häufigerer und längerer Kettenbildung). 1 x Nachspielen verwehrt allerdings die Teilhabe an praktisch mühelosem Gewinn mit deutlich längeren Serien, die es ja auch ab und zu gibt. Ein einfaches Hilfsmittel für die "Chaosphase" ist die Umformung der realen Permanenz durch weitere "Märsche", die diese Phasen in für den Spieler begreifbare Plus/Minus-Folgen verwandeln (und damit nebenbei den aktuellen Charakter der Permanenz verdeutlichen). Diese müssen dann jedoch, trotz scheinbar gewandelt "einfachem" Aussehen wieder wie oben beurteilt werden. Diese Maßnahmen sind aber lediglich ein solides Fundament, damit man sich wirksam einbilden kann, man wisse, was gerade geschieht. Der nächste gefallene Coup wird die Wahrheit unbestechlich enthüllen. Gruss elementaar
- 5.148 Antworten
-
- ec
- intermittenz
-
(und %d Weitere)
Getaggt mit:
-
au contraire (à le = au) im Gegenteil
- 5.148 Antworten
-
- ec
- intermittenz
-
(und %d Weitere)
Getaggt mit:
-
Hallo @starwind, mit Freude lese ich Deine Zeilen. Die Klarheit Deiner Gedanken, und wie Du sie ausdrückst, wird hier, wie ich hoffe nicht nur von mir, schmerzlich vermisst. Verständlich allerdings, daß, wenn man scheinbar gezwungen ist, dasselbe immer wieder schreiben zu sollen, daß man sich dann zuweilen den gerade wichtigeren Dingen zuwendet. Meine Frage nach dem Serienverhalten sollte bloß, auch zum wiederholten Male, über die darin enthaltene Banalität hinausweisen. Asymmetrie entsteht durch mindestens einen größeren Teil und mindestens einen kleineren Teil. Der größere Teil erscheint häufiger, produziert kleinere Abweichungen und bildet häufiger und länger anhaltende Serienerscheinungen seines Charakters. Soweit, so banal. Der kleinere Teil erscheint entsprechend seltener, produziert größere Abweichungen und bildet seltener und kürzer anhaltende Serien seiner Art. Wenn es nun aber doch einmal zu einer längeren Serie des kleineren Teils kommt, so ist das ganz wesentlich außergewöhnlicher, als wenn dies der größere Teil veranstaltet - man kommt schneller in den Bereich des "unverdienten" Glücks. Auch dies natürlich nichts Grundstürzendes - man sollte es aber nicht ganz aus dem Sinn verlieren. Viele herzliche Grüsse! elementaar
- 5.148 Antworten
-
- ec
- intermittenz
-
(und %d Weitere)
Getaggt mit:
-
Hallo @Chemin de fer, vielen Dank für Deine erläuternde Antwort. Es mag durchaus sein, daß ich eine Spur zu heftig reagiert habe, und das, was bei notwendiger Konzentration und Zuspitzung des Textes untrennbar mitgedacht und als Hintergrund gesehen werden muß, diesmal sträflich vernachlässigt habe: das bedaure ich und bitte um Entschuldigung. Dieser Schlüsselsatz machte es mir besonders deutlich: Vor diesem Hintergrund stimme ich Deinen Aussagen vollständig zu, und schreibe das auch seit Jahren. Aber ja doch - selbstverständlich, was denn sonst. Aber ja doch - selbstverständlich, was denn sonst. Die raunenden Karottenschwenker sind doch relativ einfach zu identifizieren, ab und zu sogar unterhaltsam, und bekümmern mich weiter nicht, sofern sie nicht die Mehrheit werden - dann bin ich eben weg. Im Kontext - ja sicher. Schaue ich mir hingegen die von Dir gezeigten Verlaufsgraphen der Permanenzumformung an, auch diejenigen aus Deinen früheren Tagen, bin ich nicht nur entzückt - sie vermitteln mir auch den Eindruck, hier sei ein "Könner" am Werk gewesen. Das Vertrackte ist leider, das Sprache, Logik, Statistik nur unzureichend in der Lage sind, Zufallsgeschehen und den Zeitpunkt seines Erscheinens hinreichend zu beschreiben, zumal ständig der menschliche Defekt dazwischen funkt, Wirkungen zu sehen, wo es keine Ursache gibt. Die "langfristig strukturierte Einsatzsteuerung" von der Du sprichst (und wie gesagt: volle Zustimmung) ist untrennbar mit der Vergangenheit verknüpft: nämlich mit der Tatsache gewordenen Satzwirklichkeit und ihrer Ergebnisse. Die aktuelle Satzhöhe richtet sich nach dem, was vorher Tatsache geworden ist. Weil unser Blick strikt auf die Zukunft gerichtet ist, und das vor jedem Coup neu, erschaffen wir mit jedem (selbst virtuellen) Satz eine persönliche Vergangenheit, die nachträglich nur die üblichen Phantasten (hätte ... wenn) leugnen. Vernünftige Leute (falls es diese Spezies gibt) reagieren. Was ich diesbezüglich unter "Vernunft" verstehe, soll ein Beispiel deutlicher machen: Spiel EC 5er-Figuren (ohne Zéro), es geht nicht um "Rot" oder "Schwarz" sondern um die Einsatzergebnisse (Plus/Minus), Spiel auf Saldo +1, Einsatz also maximal 5 Sätze. 32 Möglichkeiten; 68,75% der Partien enden mit +1 16 davon +1 nach dem ersten Satz. Ende der Partie. 16 davon -1 nach dem ersten Satz 8 davon Saldo 0 nach dem zweiten Satz. immerhin 5 von diesen 8 können +1 nach maximal 3 weiteren Sätzen noch erreichen. 8 davon aber Saldo -2 nach dem zweiten Satz. nur noch eine einzige Partie von diesen acht kann noch mit +1 enden. Aus meiner Sicht: wer bei diesem Spiel bei Saldostand -2 keine Maßnahmen ergreift (sei es per Automatikroutine oder per Augenblicksentscheidung) handelt "unvernünftig". Nebenbei: ein einfacher Test, ob man mit einem positiven Erwartungswert setzt. Die Anzahl der jeweils ersten Sätze muß mit mehr als 16/32 +1 ergeben. Die Anzahl der jeweils zweiten Sätze muß mit mehr als 8/16 0 ergeben. Zeitlich immer noch limitiert. Gruss elementaar
- 5.148 Antworten
-
- ec
- intermittenz
-
(und %d Weitere)
Getaggt mit:
-
Lieber und geschätzter @Chemin de fer, leider bewegt sich Dein letzter Beitrag in Wort und Ton wieder in den diesem Forum eigenen Bahnen mehr oder minder gemilderter Apodiktik, besonders ausgeprägt bei Sachverhalten, die niemand, auch nicht der Gerade-Sprecher, mit letzter Stringenz überblicken kann - und der geht so: "wenn Ihr nicht ganz genau meiner Ansicht seid - und allein das Hinterfragen der Ansicht ist Ausdruck Eures wirren Hirns - dann seid Ihr nichts anderes als Wundergläubige mit nicht ernstzunehmender Gehirnverdrahtung. Muss das wirklich sein? Eine Diskussion ist natürlich mit dem so Geschmähten sofort beendet, aber was soll die Veranstaltung? Als Beispiel (und ich will das gar nicht wirklich diskutieren, es ist ein Beispiel): der Differenzsatz. Vorausgesetzt wird: wer beim klassischen Roulette längere Zeit im Plus bleiben will (womöglich ein Spielerleben lang), für den bietet sich der Differenzsatz als eines der einfachsten Hilfsmittel an, und wahrscheinlich wenden wir ihn alle, in mehr oder minder expliziter (auch virtueller) Form an. Progressionen gehören natürlich auch dazu. Darin aber das alleinige Mittel zu sehen und das deshalb, ausgerechnet mit dem Argument, weil man eben nicht wissen könne, was der Zufall im nächsten Coup macht, ist dann doch etwas zu schlicht, weil es die unbedingt zu vermeidende große Zahl hinterrücks wieder importiert. Etwas plakativ: was machen denn die Differenzspieler, wenn ab sofort die nächsten 400.000 Coups nur noch das Nicht-Gesetzte kommt? Nach der reinen Zufallslehre ist das zwar sehr unwahrscheinlich, bleibt aber möglich. Und diese Möglichkeit (nicht ob, sondern wann) sollte allein schon für gehörige Demut sorgen. Zu dem hier immer geschmähten, in den Bereich des Knallköpfigen gerückten "Permanenzlesen" habe ich mich vor Jahren geäußert, ich will das nicht wiederholen. Es scheint mir nur absurd, wenn ich sehe, es kommt verstärkt die "1" (sie hat also lokal einen positiven Erwartungswert), es NICHT mit ein paar Sätzen (Kosten-Nutzen- Rechnung) auf "1" zu versuchen; natürlich nicht immer (große Zahl), natürlich nicht immer gleich lang (wieder große Zahl), natürlich nicht immer in gleicher Situation (lokales Umfeld --> große Zahl). Ob man trifft, zeigt sich für uns alle nach Kugelfall, und mit dieser dann Tatsache muß man umgehen können. Das ist das Wichtige Und nicht, was man sich vorher überlegt hat. Das klassische Roulette ist so gesehen also immer eine Art von Vergangenheitsbetrachtung. Und die Frage bleibt: was fangen wir damit an. Mal abgesehen davon, das unterschiedliche Leute unterschiedliche Zielsetzungen haben, ohne deshalb zwangsweise esoterische Romantiker zu sein. Die schon öfters zitierte Veranstaltung von @Egoist und @Feuerstein auf einem Dutzend, beispielsweise, war spieltaktisch auch für mich interessant - da ich aber auf die Rendite schaue, und nicht, ob ich "irgendwie" ins Plus komme, für mich von limitiert praktischem Nutzen. Der Gedanke allerdings, da seien zwei Idioten unterwegs, kam mir nicht - wie denn auch, das sind sie gewiss nicht. Falls mein Argumentieren nicht klar genug ist, kann ich, auf Nachfrage, noch einen weiteren Anlauf nehmen; jetzt muß ich allerdings erst mal Schluss machen - andere Aufgaben warten. Gruss elementaar
- 5.148 Antworten
-
- ec
- intermittenz
-
(und %d Weitere)
Getaggt mit:
-
Hallo @Chemin de fer, Dein Beitrag hat mich gefreut. Danke. Um einmal die, meiner Meinung nach, wichtigsten Feststellungen untereinander zu schreiben: Da stimme ich vollkommen mit Dir überein, wobei ich bei Struktur insofern ein Fragezeichen setze, als damit lokale (und nur um diese kann es ja gehen) nicht mitgemeint sind. Die Erwartung einer immerwährenden Wenn-Dann-Beziehung wird enttäuscht werden. Aber u.a. darum ging es mir: wir spielen real nur wenn wir uns ganz blöd anstellen in der großen Zahl. Auch Deine Schlussfolgerung ist, in meinen Augen, überhaupt kein Gegensatz. Es gibt aber unterschiedliche Wege, wie man die erwünschte Asymmetrie hinbekommt. Da ich EC nur extrem selten spiele, mich u. a. deshalb auch nicht wirklich wohl dabei fühle, kann ich, persönlich, nur soviel sagen, daß mir lediglich zwei Läufe leider zu wenig sind. Meine Bewunderung haben die Spezialisten allemal. Mir jedoch fehlen dazu eindeutig Können, Geduld und Nerven. Ist vielleicht auch eine Typfrage. Jeder halt wie er kann. Und bei den von mir bevorzugten mehrfachen Chancen muß man, wieder nur meiner Meinung nach, im Aussehen etwas anders vorgehen. Das Prinzip ist allerdings dasselbe. Einen schönen Restsonntag wünsche ich Dir auch! elementaar
- 5.148 Antworten
-
- ec
- intermittenz
-
(und %d Weitere)
Getaggt mit:
-
Hallo @Hans Dampf (von), hallo Sir Copilot, vielen Dank Euch beiden - das ging ja sehr schnell. Diese Zusammenfassung ist sehr gut gelungen. Für ein praktisches Spiel bleibt aber noch sehr viel Arbeit, die, naturgemäß, in einer Zusammenfassung zwar enthalten, aber so nicht sichtbar ist. Zwei Punkte möchte ich, wieder beispielsweise und willkürlich, ansprechen: die Verlaufsentwicklung hin zur "Schieflage" und wieder davon weg. Meiner Ansicht nach muß das von jedem Spieler selbst trainiert werden - eine Abkürzung ist mir nicht bekannt. Die 10.000-Stundenregel könnte hier zutreffend sein. was kann man mit der ganz richtigen Feststellung von @starwind (herzliche Grüsse!) anfangen, daß häufigere Erscheinungen geringere Abweichungen (Coupzeit) produzieren? Wie sieht es mit der Serienbildung dabei aus? Das wünsche ich Euch beiden auch. Danke. Gruss elementaar
- 5.148 Antworten
-
- ec
- intermittenz
-
(und %d Weitere)
Getaggt mit:
-
Was aber wieder nur mit der großen Zahl und ohne positiven Erwartungswert gilt. Um dieser ewig langweiligen und vollkommen unfruchtbaren Diskussion um Durchschnittswerte zu entkommen, schlage ich, zum wiederholten Mal, ein einfaches Experiment vor: rollierende Betrachtung eines, beispielsweise, 11-Coup-Fensters Verhältnisbetrachtung von Rot-Schwarz über, beispielsweise, 1000 Coups Aufzeichnung des Verlaufsgraphen über diese 1000 Coups des rollierenden 11-Coup-Fensters Wem dabei nichts Zündendes auffällt, muß sich eben etwas Anderes ausdenken. Es geht bei diesem Experiment gar nicht so sehr um die Frage, was man richtig vorhersehen kann, als vielmehr, was kann man mit den festgestellten Fakten für sein Spiel anfangen. Gruss elementaar
- 5.148 Antworten
-
- ec
- intermittenz
-
(und %d Weitere)
Getaggt mit:
-
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Ganz gewiss nicht. Was soll die Frage? Und warum schon wieder so patzig? Es war die Rede von Sir copilot - inwiefern gibt es Anlass, daß ER das auf SICH bezieht? -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Richtig. In Sachen Permanenzentwicklung wollte ich nicht darauf verzichten. Das Stichwort "Schneidungen" wollen wir dann schon mal gar nicht erwähnen. Ich bin wirklich gespannt, was Sir copilot an Programmierung zustande bringen wird. Bisherige Selbstversuche mit ihm und python waren eher ernüchternd; sowohl, was Lauffähigkeit angeht, wie codezeilen-Sparsamkeit. Aber er lernt ja jeden Tag dazu. Daß das Betrachtungsfenster bei 222 Coups (6x37) liegt, scheint bei ihm jedoch noch nicht angekommen zu sein. -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
F0 Zählung fehlt. Unklar: wird nach jedem Coup rolliert oder nach 37? Nicht geklärt: welche der unterschiedlichen Hallertabellen enthalten denn die richtigen "EW"? Rätselhaft: warum fragt ER nicht SEINEN "ein" Programmierer? -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
aller! Quelle: https://spirituelles-bewusstsein.net/die-superkraefte-des-geistes-was-macht-einen-mental-starken-menschen-wirklich-aus/ oder so ähnlich. Ein Geist des Weine(n)s wird helfen.