elementaar

Hallo @Chemin de fer, Volle Zustimmung. Mir sind überhaupt nur zwei Methoden bekannt, die nicht den natürlichen Schwankungen unterliegen. je ein Stück auf alle 37 Zahlen, mit dem völlig schwankungsfreien Ergebnis von -2,7% vom Umsatz in jedem Coup (schon die Variante je 18 Stück auf gegensätzliche EC mit einem Stück auf Zéro produziert aber durchaus schon Schwankungen). man ist der Dämon, der mit der Sicherheit 1 (eins!) jede nächste Zahl bis in alle Ewigkeit richtig und fehlerfrei vorhersagt. Alle anderen Methoden, nach meinem Kenntnisstand und egal wie viel sie erwirtschaften, unterliegen Ergebnisschwankungen. Es gab hier vor Jahren auch einmal ein Thema, wo ansatzweise Einiges dazu zusammengetragen wurde. Gruss elementaar

Hallo @Take_7, zwei Anmerkungen und eine Nachfrage. Nein, gerade nicht "im Prinzip". Es handelt sich um tatsächliche Durchschnittswerte, gewonnen durch Bildung einfacher arithmetischer Mittelwerte (Summe der betrachteten Zahlen (Orte) geteilt durch ihre Anzahl). Keinerlei Gewichtung fließt in die Hallerschen Tabellen ein. Ich sprach von Sätzen (= real von mir platzierte Stücke), nicht von Coups. Ich habe keine Angabe darüber gemacht, wieviele Coups während dieser Phase gefallen sind ("Wartecoups"). Rechnest Du nahe 800 Sätze in Pleinrotationen um (800/37) kommst Du auf über 21 Rotationen. Aus meiner Sicht IST das heftig! Zu Bedenken ist jedoch: Je länger man reale Sätze tätigt, desto unwahrscheinlicher wird es, daß man auch solch ungewöhnlich starke Schwankungen NICHT erlebt, auch bei einem Spiel mit positivem Erwartungswert. Persönlichkeiten, die sich eher auf der Weichei-Seite des Spektrums befinden, werden große Probleme damit haben, solcherart "Prüfungen" erfolgreich zu bestehen. Die Nachfrage (ohne irgendeinen polemischen Unterton): Was erscheint Dir denn in dem von Dir zitierten Textstück nicht restlos "logisch" und was ist Dir darin nicht "ganz klar"? Da ich auch beim wiederholten Lesen nicht in der Lage bin, den logischen Spalt, den Du entdeckt zu haben glaubst, zu erkennen, bitte ich um Aufklärung. Gruss elementaar

Hallo @Take_7, danke für Deine teilnehmende Rückmeldung. Eine der zahlreichen Gehirnvernebler hast Du benannt: die MITTELWERTbildung, deren Auftreten (in vielerlei Verkleidung) nicht erkannt und deren Folgen entweder nicht verstanden oder nicht ausreichend mitbedacht wird. Ein gutes Beispiel ist die Binomialverteilung: ich wüsste nicht, was man mit einer "mittleren" Bestimmung des Ortes wie der Anzahl der Teilnehmer im nächsten Coup eigentlich anfangen soll. Etwas besser sieht es aus, wenn man, Coup für Coup, die qualifizierten Einzelwahrscheinlichkeiten und vor allem deren Folgen für die Serienbildung betrachtet, und dabei ausschließlich das aktuelle Permanenzgeschehen zum Maßstab macht. Aus meiner Sicht ganz entschieden nicht nur "im Prinzip", sondern tatsächlich und, wenn Du so willst, ausschließlich. Mit dem Wissen, daß Zufall zwanghaft Muster bilden MUSS, ist das Identifizieren der Muster ja vergleichsweise einfach, in jeden Fall aber ENDLICH. Damit hat man sich aber bloß einen Überblick verschafft, was bei einer bestimmten Coupstrecke möglich ist (und damit auf lange Distanz auch eintreffen wird). Feststellung: auf einer vorher bestimmten Permanenzlänge bilden sich endliche, vollständig abzählbare Muster. Und mehr geht auch nicht; damit ist Zufallsgeschehen als ein simples Spiel der Kombinatorik (mit jeweils eigenen Wahrscheinlichkeitserwartungen) identifiziert, und ein Ende des "Zufalls" erreicht (auch Zufall kann nichts "Unmögliches"). Verkürzt und aus meiner Sicht: ENDE der Betrachtung des Möglichkeitsraums. Ganz wesentlich ist die logisch zwingende Schlussfolgerung aus dieser Betrachtung: nicht die Muster an sich sind potentielle Gewinnbringer, sondern ihre FUNKTION im jeweiligen Permanenzumfeld, denn, das ergibt sich ebenso zwingend aus der Gleichwahrscheinlichkeit der kombinatorischen Muster, sie selbst KÖNNEN die notwendige Information nicht in sich tragen, ob im nächsten Coup "Rot" oder "Schwarz" zu setzen ist. Es ist also ganz unsinnig bspw. die vier 2er-EC-Figuren in der Hoffnung auf Erleuchtung anzustarren, sie können, für sich genommen, keine Information darüber enthalten, wie es im nächsten Coup weitergeht. Ja. Ja. Nein. Ob sich dies bei konsequentem EC-Spiel erreichen läßt, halte ich für möglich, vermag es aber aus eigener Erfahrung nicht zu sagen, da ich überwiegend Mehrfachchancen spiele. Bisher ragt als Einzelfall eine Satzstrecke nahe 800 Coups heraus, bis ich wieder ein neues Allzeitsaldohoch erreicht hatte. Schlimm genug, aber mit vorsichtiger Möglichkeitseinschätzung noch nicht das Ende der negativen Fahnenstange. Die Knappheit der letzten drei Antworten spiegelt dabei wider, für wie relevant ich die Verquickung meiner persönlichen Spielmethoden (oder die anderer verständiger Mitdiskutanten) mit dem Diskussionsthema selbst halte. Gruss elementaar PS: Danke @Juan del Mar für die Klarstellung, es ist halt immer wieder zu absurd.

Vielen herzlichen Dank an alle, die sich themenbezogen geäußert haben, für Eure sowohl kenntnisreichen wie nachsichtigen Reaktionen. Erfreulich und überraschend, fast überwältigend, daß sich eine ganze Reihe von aufmerksamen Beobachtern und Gehirnbenutzern versammelt, wenn man das Forum fast schon abgeschrieben hat. Bemerkenswert erfreulich auch, daß jeder von Euch meine Illustrationsbeispiele als das verstanden hat, was sie sein sollen: Illustrationen zur Verdeutlichung, nicht exakte Handlungsanweisungen. Bspw. würde man sich bei der Binomialverteilung in der Praxis natürlich nicht mit arithmetischen Mittelwerten des Erscheinens zufrieden geben, sondern das gewichtete Erscheinen in jedem Coup verwenden, um dort eine von ferne ähnliche Ungleichverteilung wie beim Coupsverbrauch der Einer und Serien anzutreffen. Selbst bei einem "Versuch" einer "Zusammenfassung" muß man halt abkürzen. Vielen Dank fürs Lesen, Verstehen und sogar einzeln Durchgehen! Gruss elementaar

Versuch einer Zusammenfassung: 1. Die berechneten Erwartungswerte stimmen beim Roulettespiel mit den statistisch ausgezählten Werten echter Zufallszahlen bei der großen Zahl sehr gut überein. Fahrlässiger Weise werden bei dieser Aussage aber die unverzichtbaren Voraussetzungen nicht im Bewußtsein behalten - sie sind jedoch entscheidend. 1.1 Da ist zum einen die Berechnung: der berechnete Erwartungswert gilt für "unendlich" viele Versuche. "Unendlich" ist aber eine Kategorie ausschließlich des menschlichen Geistes. In der Natur, nennen wir es hilfsweise "Realität", gibt es sie nicht; nicht nur in Folge dessen ist sie der menschlichen Erfahrbarkeit entzogen, und zwar in einem Ausmaß, das einige Beispiele verdeutlichen sollen. "Unendlich" viele Versuche bedeuten u. a., daß sich "innerhalb" dieser Strecke eine Passage finden läßt, die Hunderttausende Coups (mithin länger als ein Menschenleben) nur "Rot" zeigt, ebenso aber auch "Schwarz" und alles was man sonst noch betrachtet. Und immer auch eine Serie gleicher Länge + 1, und davon wieder eine + 1 usf. Das bedeutet "Unendlich". Sämtliche schon geschriebenen Meisterwerke der Weltliteratur sind in "Unendlich" enthalten, alle noch zu schreibenden aber auch, genauso wie jeder mögliche Schwachsinn, vergangener wie zukünftiger. Falls es die "das-erklärt-alles"-Weltformel gibt, ist sie in "Unendlich" enthalten, man muß sie nur finden. Das wäre ein brute-force-Angriff der potentiell niemals endet. Das bedeutet "Unendlich". Man muß sich das einmal drastisch vor Augen führen: würden wir tatsächlich einer paar-Hunderttausender-Rot-Serie ansichtig (Millionen, Milliarden, was man will, geht auch!), eine Serie, die seit Generationen nicht abbricht, sämtliche Kessel überprüft, jeder Betrug ausgeschlossen, außer den unvermeidlichen Widerspruchsgeistern, die auf Abbruch setzen, alle Dauergewinner, dann aber sämtliche Spielbankbetreiber schon längst bankrott wären, wir müssten letztlich an der Richtigkeit der Wahrscheinlichkeitsrechnung zweifeln. Für uns, mit den Erfahrungen von Generationen vor uns, wäre Roulette ein Spiel mit zwar 37 Ergebnismöglichkeiten wie im Kessel sichtbar abgebildet, bei dem aber immer nur dieselben 18 tatsächlich herauskommen. Und würden damit ein komplett falsches Weltbild haben. Zufall in Verbindung mit "Unendlich" kann das. Zum Glück ist das Antreffen einer solchen Serie nicht sehr wahrscheinlich. Als Hilfsgrösse zum Rechnen hat sich "Unendlich" bewährt, keine Frage, man darf aber niemals den Fehler machen sie tatsächlich für "real" zu halten. --Spaßeshalber: wir können mühelos Zahlen hinschreiben, die größer sind als es Teilchen im Universum gibt - wie "real" soll das denn sein? Wenn man nicht aufpasst, kann man allein daran schon irre werden.-- Sehr real ist jedoch der nächste Coup und dessen Ergebnis: niemals wird man mit Erfolg sein gesetztes und verlorenes Stück zurückfordern können, "weil" die bestens berechnete Wunschzahl dann doch nicht gekommen ist. "Der nächste Coup" und "Unendlich"; es sollte, auch mit äußerst limitierten Geistesgaben, unmittelbar einleuchten, daß man diese beiden, in ihren Eigenschaften so extrem unterschiedlichen Ereignisse, nur mit einem enorm großen, dazu ständig präsenten Hintergrundwissen irgend sinnvoll zusammenspannen kann. 1.2 Andererseits haben wir die Ergebnisse statistischer Auszählungen von echten Zufallszahlen: sie nähern sich früher oder später den errechneten Sollzahlen prozentual an; sie scheinen damit sowohl die Richtigkeit der Rechnung als auch die Zuverlässigkeit des Zufallsgenerators zu bestätigen. Ist man aber dieser Auffassung, muß zwingend das unter 1.1 Gesagte mitgedacht werden. Obwohl diese Auszählungen immer gemacht werden müssen, ist der mit ihnen, im Vergleich zur theoretischen Überlegung in 1.1, erzielte zusätzliche Erkenntnisgewinn gering. 1.2.1 Auf (mindestens) einen Haken bin ich allerdings selbst da gestoßen: auf Anregung von @Shotgun habe ich mir das Verhalten direkter Gegensatzpaare bei den Figuren der einfachen Chancen angesehen (bspw. SSS und RRR bilden ein direktes Gegensatzpaar etc.). Beginnend mit der 3er-Figur bis zur 13er-Figur, habe ich die Erscheinenshäufigkeit der Gesamtheit der Gegensatzpaare ausgezählt, und dabei festgestellt, daß, verblüffender Weise, die Anzahl der Unterschiede des Erscheinens nicht nur absolut größer wird, sondern auch prozentual stabil abweicht. Je länger die Figurenpaare dabei gewählt werden, desto stabiler, aber auch geringer ist dabei die prozentuale Abweichung. Der Betrag der Abweichung (13er-Figur: ca. 0,9% vor Zéro) reicht dabei nicht, um den Auszahlungsnachteil zu egalisieren, gibt aber einen Hinweis, daß es selbst in der großen Zahl nicht gänzlich aussichtslos ist, eine gewinnfähige Strategie zu konstruieren. 2. Aus 1. ergibt sich nahezu zwingend: ein möglicher Dauergewinn beim Roulettespiel muß auf jeweils sehr kurzer Spielstrecke realisiert werden. Das leuchtet unmittelbar ein: kein Mensch kann "unendlich" lange spielen, kein Mensch hat (selbst ohne Tischlimit) "unendlich" viel Kapital, selbst im scheinbar günstigen Fall von bspw. 1%iger Überlegenheit: kein Mensch wäre in der Lage, die allfälligen Schwankungen dauerhaft auszuhalten. (Die beim Roulettespiel im Schnitt etwas über 2% liegende Überlegenheit der Spielbankbetreiber markiert dabei die untere Grenze, die ein einzelner Spieler mit seinem Spiel mindestens übertreffen muß.) 2.1 Ich schreibe "möglicher" Dauergewinn beim Roulettespiel und muß sofort präzisieren: daß dies abstrakt "möglich" ist, beinhaltet ja gerade die Unendlichkeitskonstruktion aus 1 (die Hunderttausender Rotserie beschert dem Rotspieler eine lebenslange Siegesserie ohne einen einzigen Fehltreffer), die Frage ist doch eigentlich eine ganz andere. Nämlich: ist es möglich aus der zweifelsfrei existierenden "Möglichkeit" etwas Tatsächliches zu machen, oder anders formuliert: ist bei reinem Zufallsgeschehen persönlich "kluges" Handeln überhaupt eine sinnvolle Kategorie, oder gilt das "inschallah" der Geht-nix-Fraktion? "Die" Mathematik jedenfalls sollten jene Glaubensjünger tunlichst außen vor lassen. Wie gerade kurz umrissen, ist die keineswegs so eindeutig, wie sie es gerne hätten. Das Argument, daß sich viele kurze Spielstrecken zu einer einzigen großen addieren, ist dabei sowohl vollkommen richtig wie vollkommen nutzlos (wie so oft bei "mathematischen" Aussagen). Um es möglichst platt auszudrücken: schließe ich jede kurze Spielstrecke mit dem Ergebnis + 1 Stück ab, kann ich addieren bis zum Sanktnimmerleinstag, und werde damit lediglich Indizien anhäufen, daß meine Spielweise selbst bei einem unfairen Spiel ganz offensichtlich einen positiven Erwartungswert produziert. Wie das dann "möglich" ist, kann wissenshungrige Geister in ihrer Freizeit jahrelang beschäftigen, ändert jedoch nichts an den Tatsachen, die der Füllstand des Geldbeutels unbestechlich abbildet. Der etwas gedankenlose Umgang mit diesem Argument ist scheinbar die Folge dessen, daß sich in den allermeisten Fällen simpler Spielvorschläge die Erwartung erfüllt, daß ein zunächst positiver Ertrag einer Strategie auf Dauer dem negativen Erwartungswert des Spiels unterliegt. Mehr ist damit aber auch nicht gezeigt: spiele ich negative Erwartungswerte, erhalte ich in der großen Zahl negative Erwartungswerte. Tatsächliches Erstaunen darüber verwundert. Und die Anforderungen sind in der Tat hoch: ein Dämon, der behauptet jede nächste Zahl vorhersagen zu können, muß nach der Clariusformel seine Fähigkeiten 38 mal in Folge demonstrieren, bevor wir halbwegs "sicher" sein können. Irrt er sich dabei nur ein einziges Mal, muß er schon knapp 400 weitere Zahlen ohne einen zusätzlichen Fehler vorhersagen. Irrt er sich dabei wieder nur ein einziges Mal, muß er in der Folge dann schon einige Tausend weitere Zahlen fehlerfrei vorhersagen. Das ist schon heftig. 2.2 Auf eines kann man sich bei reinem Zufallsgeschehen allerdings verlassen: auf kurzen Spielstrecken müssen sich Verdichtungen und Dehnungen der Einzelereignisse bilden, anderenfalls wäre es kein Zufall mehr. Beispiele sind Binomialverteilung, Bifurkation, Sierpinskidreieck. Für alle gilt: WEIL für jedes Einzelereignis ein bestimmter Erwartungswert nicht nur "erwartet" sondern auch real eingehalten wird, MUSS sich das jeweils charakteristische Muster bilden, je häufiger ("unendlich") die Versuche, desto deutlicher. Niemals kann es dabei zu einer statistischen Gleichverteilung kommen. Die obig herbeiphantasierte Hunderttausender Rot-Serie wäre, auf kurze Strecke heruntergebrochen, lediglich eine extreme Verdichtung. Die einfachen Chancen (EC) haben eine einzigartige Eigenschaft: ihr jeweiliges Gegenteil ist genau gleichgewichtig, sowohl in der Erscheinenswahrscheinlichkeit, wie der Auszahlung. Eine bspw. 3er-Figur kann nur auf zwei Arten im nächsten Coup zur 4er-Figur werden. Da aber auch 4er-Figuren gleichwahrscheinlich sind, wird sofort klar, daß unsere Satzweise in der Praxis gewährleisten MUSS, daß beim Anblick einer bestimmten 3er-Figur mal die eine Chance und mal das Gegenteil zu setzen ist. Mit einfachem Raten, welche der beiden Möglichkeiten im nächsten Coup zu bevorzugen ist, wäre aber auch nichts gewonnen (Zufall gegen Zufall), denn damit unterliegen wir sofort dem Erwartungswert der Chancengröße. Die nötigen Informationen zum qualifizierten Raten liegen somit ganz offensichtlich im Permanenzverlauf, in der mehr oder minder langen Historie der praktischen Spielsituation, in der wir uns gerade befinden. Der Spott schlichter Gemüter über das "Permanenzlesen" und die Gedächtnislosigkeit der Kugel demonstriert dabei nur, daß, mal wieder, eine wichtige Eigenschaft des Zufalls "vergessen" wurde: der Zwang zur Musterbildung. Nochmals: WEIL für jedes Einzelereignis ein bestimmter Erwartungswert nicht nur "erwartet" sondern auch real eingehalten wird, MUSS sich das jeweils charakteristische Muster bilden. Ein Gedächtnis ist dafür nicht erforderlich, sondern lediglich zufälliges Erscheinen gemäß der Chancengröße. Dabei ist die Musterbildung an sich nicht gewinnfähig (als FOLGE des negativen Erwartungswertes), daß die Muster sich allerdings bilden MÜSSEN, ist eine TATSACHE. Die 5er-Figur der EC (1/2^5 = 1/32) verhält sich recht ähnlich der Einzelzahl (EZ = 1/37), mit Recht sagt also der "Permanenzleser" voraus, daß sich ca. in Coup 6 eine bisher erschienene 5er-Figur zum zweiten Mal zeigen wird. Seine Vorhersage wird dabei umso genauer, je öfter er sie macht. Vergleicht er also nach Coup 5 die beiden Möglichkeiten, wie die letzte 4er-Figur zur 5er-Figur werden kann, hat er eine qualifizierte Handhabe für seine Entscheidung: eine gänzlich neue Figur würde einen Wartecoup signalisieren, ebenso wenn beide Möglichkeiten einen ersten Figurenzweier ermöglichten, ansonsten das Eine oder eben das Andere setzen. Das damit auf Dauer nicht gewonnen werden kann, sollte klar sein (nach wie vor negativer Erwartungswert), es ist aber ein einfaches Beispiel für "Permanenzlesen" - und hoffentlich Verdeutlichung und Anregung. Die Genauigkeit des vorhergesagten Ortes, wann ein Ereignis stattfinden wird z.B., erhöht sich in der Binomialverteilung durch die Verringerung der Einzelwahrscheinlichkeit. Was spricht also dagegen sich einmal das Verhalten von 13er-, 21er oder 35er-Figuren anzusehen? Und diese Vorhersagen bspw. mit vdW zu kombinieren? Natürlich sind die Aussichten damit nicht gut: ein negativer Erwartungswert + ein weiterer negativer Erwartungswert ergibt schließlich wieder einen negativen Erwartungswert. Womöglich begegnet einem aber auf dem Weg dorthin eine Einsicht, die weiterführt. 2.3 Ein paralleler Ansatz besteht darin, sich die Umsatz/Saldo-Entwicklung verschiedenster Spielanweisungen als eine Art Film vorzuführen (auf Youtube gab es verschiedentlich solche Filmchen, wenn man es nicht selber programmieren möchte). Dabei wird man schnell bemerken, daß es bei buchstäblich jeder Spielanweisung Phasen eines steilen (relativen) Gewinnanstiegs gibt. Offensichtlich haben wir in solchen Phasen einen POSITIVEN Erwartungswert (es wird ganz wesentlich mehr gewonnen als verloren), und diese Phasen bilden sich zwanghaft, weil Zufall nun einmal ist, was er ist. Und nur in diesen Phasen ist ein reales Setzen überhaupt sinnvoll. Es ist einfach absurd, in den Phasen des steilen (relativen) Saldoabstiegs, aber auch in Phasen der Seitwärtsbewegung (immer noch negativer Erwartungswert) überhaupt nur ein einziges Stück zu riskieren. Gewinnforschung beim Roulettespiel muß sich also darauf konzentrieren, wie man zuverlässig und möglichst schnell jene Phasen eines steilen (relativen) Gewinnanstiegs identifiziert und per realem Setzen für sich ausnutzt, egal bei welchem Spielvorschlag und egal welcher Chancengröße. (Daß man außerdem den Abbruch der Gewinnphase ähnlich zuverlässig und möglichst schnell identifizieren muß, versteht sich in dieser Betrachtungsweise von selbst.) 2.4 Die rohen EC-Salden haben leider die unangenehme Eigenschaft, daß sie die allermeiste Zeit in Seitwärtsbewegungen verbringen. EC-Spieler, die es nicht hinnehmen wollen, daß mindestens 60-80% ihrer Coups- (und damit Lebens-)zeit mit Uninteressantem verschwendet wird, sind also schon deswegen gezwungen, die vorhandene Permanenz mit mehreren parallelen Scheinspielern jeweils anders aufzubereiten. Klug ausgewählt können sie zudem auch nicht offensichtliche Periodenbildung (Schwingung, Rhythmus wären andere Worte desselben Phänomens) zugänglich machen. Die Selbstähnlichkeit der Fraktale können ebenfalls sichtbar gemacht werden. Gruss elementaar

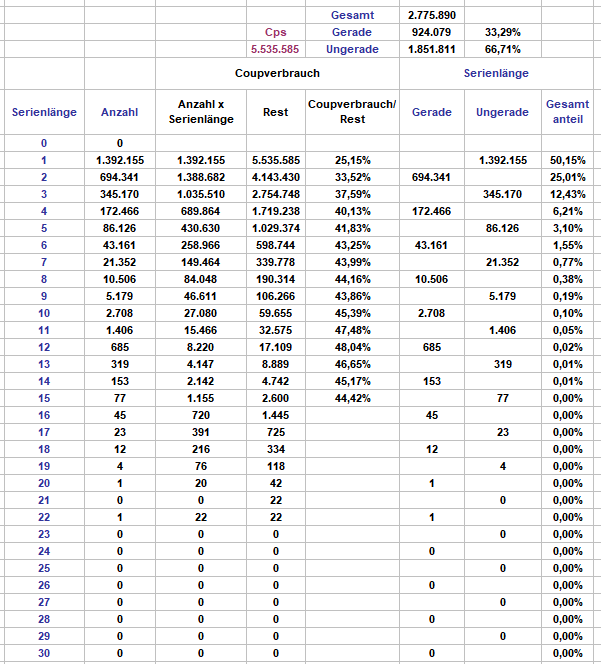
Hallo @Hans Dampf, es geht bei dieser Frage aber gar nicht um Anzahlen, Folgen oder Wechsel, sondern einfach um den Coupverbrauch. Die Frage lautet schlicht: Wieviele Coups werden verbraucht mit Einern (Nase oder Kette) und Serien (egal wie lange, ob isoliert auftretend oder in Kette, auch egal, ob die "Farbe" zwischen den Serien wechselt (sonst kann es keine Kette werden))? Die Antwort auf diese schlichte Frage (sowohl empirisch wie rechnerisch) lautet: die Einer verbrauchen ca. 25% der Coups, die Serien verbrauchen ca. 75% der Coups. Ob das nun "bledzin", in welcher Potenz auch immer, ist, kann jeder für sich selbst beurteilen, jedenfalls ist es eine Tatsache, die man hinnehmen muß. Jeder parallel zur Permanenz und virtuell gespielte Marsch zeigt mit seinen Plus/Minus-Folgen ein ähnliches Coupverbrauchsverhalten. In ihrer Gesamtheit sind sie geeignete Hilfsmittel, um die aktuelle Permanenz besser beurteilen zu können und das eigene Spiel entsprechend anzupassen. Denn nur darum geht es im praktischen Spiel: auf sehr kurze Strecke mehr richtig als falsch zu "raten". Beste Grüsse elementaar

Hallo @benjo, vielen Dank fürs genaue Lesen! Und ja, den zitierten Satz kann man zweifelsohne so verstehen, würde in meinem Fall aber doch daneben liegen. Ich verkaufe in dieser Hinsicht nichts. Die betreffende Textpassage sollte andeuten, was jeder Auftragnehmer kennt: Kunden wissen oft nicht so ganz genau, was sie eigentlich wollen, oder, fast noch schlimmer, haben sich die Auswirkungen dessen, was sie wollen, etwas anders vorgestellt, was mehr oder minder latente Unzufriedenheit beider Seiten bewirkt. Engagierst Du einen Programmierer auf Stundenbasis wirkt das auf beide Seiten beruhigend. Meine ganzen Spielbankprogrammierungen sind aus purem Wissensdrang (wie verhält sich (Roulette-)zufall?) über Jahrzehnte zusammengekommen, nicht weil mir Programmieren an sich so besonders viel Spaß macht, sondern einfach weil man das richtige Werkzeug zur jeweiligen Aufgabe braucht. Wenn also jemand nach etwas Speziellem fragt (und jeder Programmierer steht irgend wann einmal auf dem Schlauch!), und ich erinnere mich, eine solche Fragestellung schon einmal zufriedenstellend gelöst zu haben, und ich finde eine Lösung mit annehmbarem Aufwand, dann stelle ich sie halt als Schnipsel hier ein. Kleine Mühe für mich, und, wenn es klappt, großer Ertrag für den Fragesteller. So sollte ein Forum (auch) sein. Wenn es nicht klappt - war einen Versuch wert, Schaden gering. Daß es sich bei Deiner Anfrage nicht um einen solchen Fall handelt, war Deinem ersten Text für mich nicht zu entnehmen, insofern ein Mißverständnis, für das ich um Entschuldigung bitte. Gruss elementaar

Hallo @benjo, leider entwickeln sich Deine Anfragen nicht so, wie ich es erhofft hatte, nämlich als "Hilfe zur Selbsthilfe". Natürlich "kann" ich eine solche Datei erstellen, und habe es auch schon längst getan, wie Dir ein halbwegs sachverständiger Blick in die ersten beiden Dateien hätte andeuten können. Die Figurennummer neben den letztgefallenen Coup bilde ich mit SVERWEIS() oder WVERWEIS() ab, dafür braucht man aber keine Verformelung der Figurenaufzählung (dritte Datei), sondern lediglich deren Werte und die Zusammenfassung in einem Term. Deine Wünsche bzgl. der Rot-Schwarz-Aufschlüsselung und besonders der Behandlung von "Zéro" machen, leider, den Eindruck des Nicht-zu-Ende-gedachten. Kein Problem, wenn Du einen fähigen Programmierer engagierst, dem ist das recht und erhöht nur dessen Stundenkonto, aber auf freiwilliger und kostenlos Basis stehe ich dafür nicht zur Verfügung. Noch ein Tip, nachdem Du die "Zéro"-Behandlung gedanklich gelöst hast: Damit im nächsten Coup eine 13er-Figur vollendet werden kann, ist in diesem Coup eine eindeutige 12er-Figur entstanden, die sich im nächsten Coup nur auf zwei Arten in eine 13er-Figur erweitern kann. Zuvor hat sich die jetzt eindeutige 12er-Figur aus einer 11er-Figur (mit wiederum genau zwei Möglichkeiten zur 12er-Figur) gebildet usf.; zurück bis zur 2er-(oder auch 1er-)Figur. Daraus lassen sich Entscheidungsbäume aufzeichnen und auch graphisch aufbereiten. Kombiniert mit den Einzelwahrscheinlichkeiten der jeweiligen Figuren und deren Binomialverteilung: ein interessantes Thema. Gruss elementaar

Hallo @benjo, meine Spielbankdateien sind mit vielen wechselseitigen Verweisen modular aufgebaut. Daraus funktionsfähige Einzeldateien zu extrahieren, ist unverhältnismäßig aufwendig - also nein, dieser Mühe unterziehe ich mich nicht. Ich habe Dir jedoch eine Datei gebastelt, die Du selbst vervollständigen mußt: Nach dem Öffnen markiere die Zellen "A6" bis "AA6". Kopiere diesen Zellenblock (per Anfasser rechts unten) bis Zeile 8196. Fertig ist die vollständig verformelte Datei für die 13er-Figur. Beim Aufschreiben evtl. anderer Figurenlängen beachte bitte, daß auch die Zellen "B5" bis "N5" verformelt sind. Gruss elementaar Variationen mit Zurücklegen_EC_13er-vervollständigenK.xls

Teil 2 Variationen mit Zurücklegen_EC_13er-Figur_Werte_02K.xls

Hallo @benjo, im Anhang die erbetene Datei. Die Figurennummer steht in Spalte "B". In den Spalten "C" bis "O" findest Du die EC pro Coup. "1" und "2" sind dabei Platzhalter für ein EC-Paar. Wegen der Uploadbeschränkung sind alle Angaben als Werte abgebildet und nicht verformelt. Und selbst damit mußten es noch zwei Teile werden. Nach dem Herunterladen bitte Datei ...02K an die Datei ...01K anhängen. Gruss elementaar Variationen mit Zurücklegen_EC_13er-Figur_Werte_01K.xls

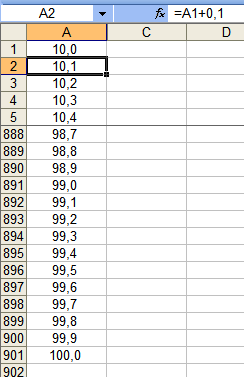
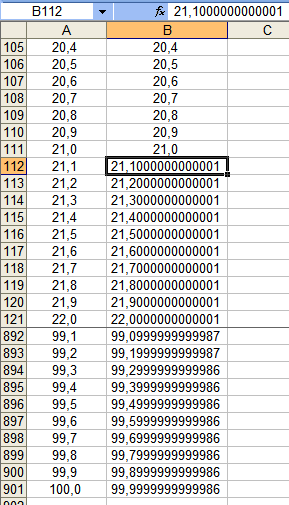
Hallo @Tüdel, welch haarsträubende Dinge Excel treibt, wenn es "rechnet", kannst Du Dir mit einem einfachen und schnellen Experiment vor Augen führen: 1. öffne eine neue Mappe in Excel 2. markiere die Spalten A und B und formatiere die Zellen als "Zahl" mit einer Nachkommastelle 3. schreibe in Zelle A1: "10" 4. schreibe in Zelle A2: "=A1+0,1" 5. fasse Zelle A2 rechts unten und kopiere diese bis Zeile 901; in Zelle A901 steht dann "100,0" Alles bestens und wie es sein soll? Könnte man glauben. 6. Markiere Spalte A und kopiere diese 7. Markiere Spalte B, rechtsklick, "Inhalte einfügen...", Werte Immer noch alles bestens? 8. Gehe in Zelle B901 und lies in der Anzeigeleiste (fx) den dort verkündeten Wert ab! In Wirklichkeit produziert Excel schon ab Zeile A112 einen Matrixfehler, den es laut eingegebener Formel (Zellen A2 ff.) gar nicht geben dürfte. (Beispiel erstellt mit Excel 2003; neuere Versionen sind nicht besser geworden, bspw: https://administrator.de/forum/excel-2010-rechenfehler-309559.html ) Ganz allgemein: softwareerstellte Zufallszahlen (Pseudozufallszahlen) sind für unsere Zwecke nicht zufällig genug. Falls Dir kein physikalischer Zufallszahlengenerator zur Verfügung steht, gibt es noch das hier im Forum oftmals beschriebene "Verfahren Wenke". Der möglichst große Zahlenvorrat, aus dem es neue Permanenzen generiert, darf allerdings ausschließlich aus echten Zufallszahlen bestehen. Gruss elementaar

Hallo @Ropro, Fragen? Bei mir bis jetzt keine. Alles sehr übersichtlich und klar dargestellt. Dankeschön! Besonders schön an Deiner Staffel finde ich, daß jede Satzstufe die jeweils gesetzten Zahlen mit dem gleichen Stückwert (1/3 Stück) belegt. In Deiner Testpermanenz bekommst Du also 11 von 12 TP zu einem zeitweiligen Plus, und das mit purem Durchspielen. Allerdings sind die -173 bei TP3 (7-9) schon heftig: bei grob 12 Stück pro Rotation sind das knapp unter 15 Rotationen! Sie werden wohl nach den +13 entstanden sein, aber dennoch: heftig (aber vielleicht auch ein Ansatzpunkt). Ich selbst kann leider erst in frühestens 4-6 Monaten wieder mitmachen - deshalb diese nur kurze Meldung. Interessant ist es schon. Gruss elementaar

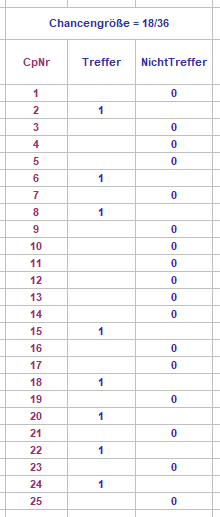
Hallo @Hans Dampf, Nur zu, nichts dagegen. Allerdings hoffe ich, daß wir uns nicht mißverstehen: oben ging es um den eher akademischen Mikrovorteil, den 1er gegenüber allen Serien bei endlicher Spielstrecke haben (und sind dabei wieder auf das altbekannte Problem des Nachweises gestoßen: "eigentlich" je endlicher, d.h. je kürzer die Betrachtungsstrecke, umso "größer" der Vorteil - aber auch desto größer die Schwankungen, die jeden Vorteil wieder zunichte machen; dieses Problem läßt sich logisch nicht restlos und einwandfrei lösen!) Als ich weiter oben von Kettenbildung sprach, bezog sich das aber ausdrücklich auf lokale Phänomene. Im Schaubild zeigt der "Treffer"-strang lokal eine Kette von 1ern im von mir angesprochenen Sinn. Diese werden sich weder häufiger noch länger bilden als Ketten von Serien jeder Länge (>1, Verhältnis 1:1), sehr wohl jedoch doppelt so häufig/lang wie Ketten von abgeschlossenen 2er-Serien (Verhältnis 2:1). Als "Marschbefehl für immer" bringt das natürlich gar nichts. Hier sieht man deutlich, daß man dieses Ketten-Verhältnisspielchen bis ultimo treiben kann. Aus meiner Sicht interessant ist das alles aber erst dann, wenn man bei "Farben"-wechsel (bei mir von Treffer zu NichtTreffer oder umgekehrt) vor der Beurteilungsfrage steht: Folge oder erneuter Wechsel. Gruss elementaar

Hallo @Hans Dampf, danke, Dir auch einen schönen Sonntag. Bleiben wir bei der Theorie, könnten sich die Hundertstel-Prozent durch Hinzunahme der kurzen Serien maximal knapp verdoppeln zu <2 x Hundertstel-Prozent. Da stimme ich Dir zu. Praktisch sind wir dann aber beim reinen Unsinn angelangt: nach erstmaligem Erscheinen eines Treffers (oder NichtTreffers) sollen wir auf 1er-Abbruch spielen, klappt das nicht, ist damit ein 2er entstanden, den wir wieder auf Abbruch spielen sollen usf. Wo hört das auf? Beim 10er Abbruch, oder beim 15er Abbruch? Während wir dann schon dem tausendstel- oder zehntausendstel-Prozent "Vorteil" hinterherjagen. Wahrscheinlich kommt dann die 16er-Serie einmal zu viel, und wir sind ein ganzes Stück los. Am oben geschilderten indirekten Nachweisverfahren kann man schon ablesen, in welchen Mikrobereichen man sich dabei bewegt. Und eines der lustigsten Vorkommnisse des 500-Milliardenabenteuers habe ich noch gar nicht geschildert: in einer der 500-Millionen-Stichprobe tauchte eine 42er-Serie auf; diese "sollte" sich erst mit 2,2 Billionen Ereignissen zeigen, -(dieses "sollte" ist natürlich purer Unfug, es gilt: innerhalb von x Coups "sollte", diese 42er-Serie war ja "innerhalb", halt etwas früh)- justament diese Stichprobe zeigte aber eine leichte Unterrepräsentation der 1er; trotz "starkem" Coupsverbrauch mit der langen Serie (schön falsch gerechnet: zur erwartbaren 30er-Serie in der Stichprobe +12 Coups [auf 500 Millionen!]), hätte man mit 1er-Abbruch satt verloren, wenn man denn 500 Millionen Coups gespielt hätte. Überhaupt das Nachweisverfahren: 1.000 Stichproben sind ja nicht viel für diese Frage. Aber gesetzt den Fall die Aussage "ca. 65% Prozent der längsten Serien erscheinen in der zweiten Hälfte" ließe sich erhärten, es sind damit ja immer nur die längsten gesehenen Serien gemeint, d.h. je länger man dies treibt, umso kleiner wird der errechnete Vorteil, und umso schwerer wird der Nachweis, bis (im Unendlichen) gar keiner mehr existiert. Gruss elementaar

Guten Morgen @starwind, Das kann ich sehr gut nachvollziehen - zumal ein sauberer Nachweis extrem mühevoll ist. Was Du über "Restungenauigkeiten" der Empirie schreibst, ist ja alles sehr richtig und einsichtsvoll. Aber genau darin liegt auch die Mühe des Nachweises, nicht etwa im bloßen Bewegen von Milliarden Zahlen, das macht der Rechner alleine. In der reinen Lehre (Mathematik) ist ja klar, daß @Hans Dampf und @Alter Schwede Recht haben (sollten). Es kann sich dabei aber, wenn überhaupt, nur um winzige Bruchteile von Prozent handeln. Wie schon geschildert, wird bei einer praktischen Überprüfung dieser These schnell klar, daß ein direkter Nachweis wegen der (auch im Milliardenbereich) unvergleichlich stärkeren, natürlichen Schwankungen nicht sinnvoll ist. Das ist Dein Gegenargument - gut erkannt und richtig. Genau deshalb bin ich einen anderen Weg gegangen. Ich habe stichprobenbezogen aufzeichnen lassen, wann die jeweils größten zu erwartenden Serien innerhalb der Stichprobe auftraten; also beispielsweise, in einer 100-Millionen-Stichprobe sind zwei >=27er-Serien zu erwarten, wann traten sie innerhalb der Stichprobe auf? Läßt sich nämlich zeigen, daß diese langen Serien überwiegend in der zweiten Hälfte der Stichprobe auftreten, ist der Nachweis erbracht. Mit den 100-Millionen-Stichproben ist das nicht zu meiner Zufriedenheit gelungen ("Tendenz" ja, aber mit zu großer Fehlerquote). In einem zweiten Anlauf habe ich dann 500-Millionen-Stichproben genommen (erwartbar: eine >= 30er-Serie innerhalb der Stichprobe). Das habe ich 1.000 mal wiederholt (gesamt: 500 Milliarden Coups). Im Ergebnis kamen die langen Serien zu, grob gerundet, 65% Prozent erst in der zweiten Hälfte der Stichprobe. Nun kannst Du einwenden, daß 1.000 Stichproben bei diesen Prozentzahlen noch deutlich zu wenig sind - und Du hättest vollkommen Recht damit. Ich will auch gar nicht behaupten (und habe es auch nicht getan) mir persönlich sei der Nachweis damit gelungen. Mit dem aufgezeigten Weg ist es allerdings möglich. Es hat sich allerdings auch gezeigt, und das überdeutlich, daß es eine rein akademische Frage ist - ein praktischer Nutzen müßte erst mal erfunden werden. Praktisch habe ich den Versuch nach dieser Zahlenmenge abgebrochen, weil die Hauptfrage, weswegen ich ihn überhaupt aufgesetzt habe, längst beantwortet war: gibt es eine "natürliche" Grenze der möglichen Serienlängen oder sind sie, wie mathematisch vorhergesagt, unbegrenzt. Es war äußerst faszinierend, dabei live beobachten zu können, mit welcher Präzision sich die mathematischen Vorhersagen erfüllen. Übrigens für Deine Skepsis und Dein Nachhaken bin ich außerordentlich dankbar: eine Diskussion der Methoden zur Wissensvermehrung findet hier viel zu selten statt. Gruss elementaar

Hallo @Hans Dampf, Das ist richtig - und es läßt sich sogar nachweisen. Die Stichproben müssen allerdings im > Milliardenbereich sein; ich habe es irgendwann gut sein lassen und kam auf Abweichungen im Hundertstel-Prozent-Bereich. Es entspricht im Ergebnis der Überlegung von @Alter Schwede. https://www.roulette-forum.de/topic/17969-denkfehler-der-mathematik/?tab=comments#comment-349786 Das ist aber leider ebenso richtig - und es kommt noch schlimmer: die Schwankungsbreite im Erscheinen der kleineren Serienlängen, also die, die auch ein "normaler" Spieler erwarten muß, ist um ein vielfaches größer. Das ist das alte Problem, daß Prozentabweichungen mit steigender Spieldauer zwar kleiner werden, auf den Tisch aber (absolute) ganze Stücke gelegt werden müssen. Da sind ein paar 3er-Serien "zuviel" wesentlich schmerzhafter, als daß das Ausbleiben einer 50er-Serie einen trösten könnte. Gruss elementaar

Oja! Du hast ja oft genug darauf hingewiesen: aus meiner Sicht muß man bei EC aus dieser 50:50 Denkfalle wegkommen - ich würde behaupten: sonst wird das nichts. Gruss elementaar

Einer der besten (klassischen) Spieler, die ich in meiner Landcasinolaufbahn je kennen gelernt habe, verkündete mir eines Tages: "Heute spiele ich nur 2er- und 3er-Abbruch." Gemeint waren Serienabbrüche auf Rot-Schwarz. Da ballistisch unterwegs, dachte ich nur "Aha". Nach anderthalb Stunden war er erfolgreich fertig, während ich noch nicht einmal angefangen hatte. Von der Seitenlinie und zum Nachdenken: Abgeschlossene 2er-Serien verhalten sich zu allen anderen Serienlängen 50:50. Altbekannt. Welche Serienlängen bilden also am ehesten Ketten von gleich langen Serien? Selbst wer an die jederzeitig sich manifestierende 50:50-Chance bei EC glaubt: was spricht denn dagegen, bei lokal gehäuft auftretenden 2er-Serien auf Schwarz auf eine Fortsetzung zu spielen? Mehr als verlieren kann man ja nicht. Spielt man IMMER auf den 2er-Abbruch sollte man sich keine Illusionen machen - aber lokal auch? Gruss elementaar

Hallo @mona13, es ist sehr freundlich von Dir, daß Du nach meiner Meinung fragst und auch noch "nett" über mich sagst. Merci! Meine Meinung ist zweigeteilt: Als Spiel auf Zeit: wie auch schon weiter oben geäußert, sollten wir genug zusammengetragen haben, daß dem aufmerksamen Leser mehrere Spielmöglichkeiten vor Augen stehen. Und insofern bin ich auch mit @Ropros sehr lobenswerter, gelungener Zusammenfassung vollkommen einverstanden. Ganz anders als Dauerspiel: hier bin ich der Ansicht, daß die spielfertige Aufbereitung des Permanenzgeschehens, wenn überhaupt, noch in den Kleinkindschuhen steckt. Die oben benannte vage Verbindung zu EC (2 Coups zu entsprechend 8 Coups pro Rotation) ist ja viel zu grob, um ernsthaft diskutabel zu sein. Dafür ist ein Pleinspiel mit seiner größeren Dynamik auch einfach zu schade; ich zumindest spiele kein Pleinspiel, um versteckte EC-Mechanismen zu exekutieren - das sollte deutlich besser gehen. Gruß elementaar

Hallo @wiensschlechtester, Einspruch angenommen. Alles richtig, was Du schreibst. Und dennoch ist mein Satz ja nicht falsch, sondern mag auch als Indiz dienen, daß ich mit EC bis heute noch nicht richtig warm geworden bin. Beste Grüsse! elementaar

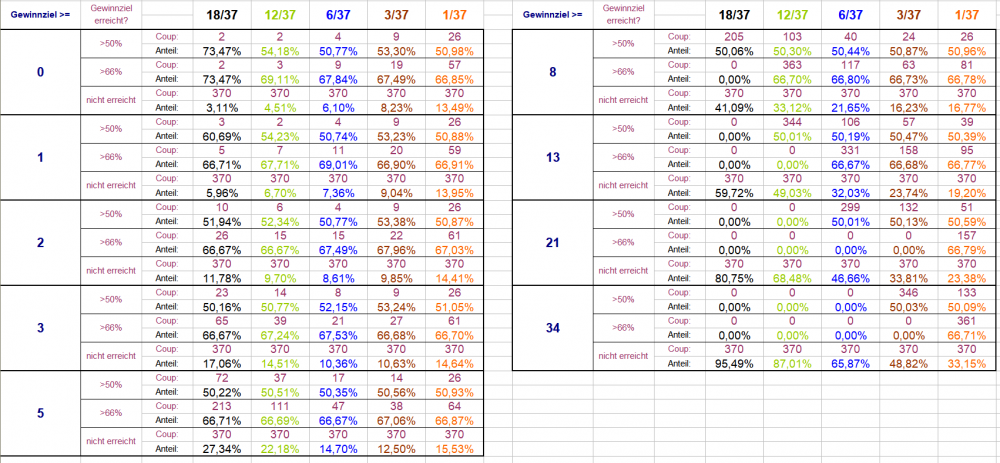
Hallo @Hans Dampf, ich sag's ja; während ich Kleinmütiger mich selbstzerfleischend nach Hause trolle, gewinnst Du ein kleines Stückevermögen. Warum kann ich das nicht auch? Es ist ein Jammer! Einen habe ich aber noch: Alle Werte mit Verfahren "Wenke" und längstens 370 Coups Spieldauer. Lesebeispiele: wenn ich wissen will, was mich erwartet, wenn ich pro Partie ein Gewinnziel von >=3 Stück anstrebe und über zwei Drittel meiner Partien erfolgreich beenden will, lese ich ab, daß 18/37 dafür 65 Coups braucht, 6/37 hingegen schon nach 21 Coups fertig ist, mit leicht höherer Quote 67,53%. wenn mein Gewinnziel >=21 Stück pro Partie ist und über die Hälfte meiner Partien erfolgreich sein sollen, lese ich ab, daß das für 18/37 nicht zu schaffen ist, während 1/37 dies nach 51 Coups erledigt, mit der Quote 50,59%. Gruß elementaar

Hallo @Hans Dampf, Ja leider, da sagst Du was. Das wäre dann Flächendegression: "Wenn ich schon nicht treffe, soll es sich wenigstens rentieren, wenn doch." Obwohl mir dieses Konzept eine Spur sympathischer ist als eine Einsatzverringerung, stelle ich mir dazu eine Geschichte vor. Nach einem langen, anstrengenden Spieltag mit ergiebigen Verlusten, hast Du nur noch zwei Stück in der Tasche. Was setzt Du? Zwei Coups EC, zwei Coups Dutzend/Kolonne oder zwei Coups Plein? Meine Antwort ist klar: ich gehe mit den zwei Stück nach Hause, und ärgere mich schwarz und tagelang, daß ich es überhaupt so weit habe kommen lassen - ein vernünftiges Spiel ist ohne sinnvolle (d.h. der bespielten Chance angemessene) Kapitalausstattung zu jedem (!) Zeitpunkt der reine Unsinn. Um bei Deinem Beispiel zu bleiben: man stößt sofort auf das Problem der Vergleichbarkeit. Das Verflixte sind die EC: muß ein EC-Spieler für sein Gewinnziel ein zweites Mal setzen, hat er damit fast eine komplette Chancenrotation Umsatz gemacht. Es gibt für ihn schlichtweg keine Möglichkeit das zu vermeiden. Nach jedem Fehltreffer steht er vor der Frage: aufhören oder weitersetzen und damit die Umsatzrotation vollenden. Und das bei einer äußerst dürftigen Informationslage, was bedeutet schon "-1" bei EC?. Um diese zu verbessern ist er praktisch gezwungen, sich die Permanenz in mehreren Strängen aufzubereiten. Die Auszählung zeigt das auch sehr schön. Gewinnziel +2; Ergebnis: Chancengröße 12/37 ist in jedem Fall zu bevorzugen. Was ist dabei mit Gewinnziel +1? Erster Satz: EC klar vorn; 12/37 muß aber noch ein zweites Mal setzen dürfen, denn bei Treffer hätte sie ebenfalls +1. Kapitalausstattung also minimum 2 Stück. Falls EC aber ein zweites Mal setzen muß, wird mit diesem Satz niemals das Gewinnziel erreicht werden können; falls also EC überhaupt ein zweites Mal setzen muß, muß sie zwangsweise auch ein drittes Mal setzen dürfen. Kapitalausstattung damit also minimum 3 Stück. Ein dritter Satz für 12/37 wiederum bedeutet bestenfalls Ergebnis "0" (bei (fast) vollendeter Chancenrotation), was für sie einen zwangsweisen vierten Satz nach sich zieht. Usf. Aus dem Obigen ergibt sich für mich zwangsläufig: Gerade für EC brauche ich ein Spiel mit stark positivem EW. Habe ich den, brauche ich keine Tricks. Richtig angewandter "Kelly" dient der Ergebnisoptimierung und fertig. Habe ich einen solchen jedoch nicht, sind alle anderen Chancengrößen ganz wesentlich besser geeignet, um mich länger vor dem Ruin zu bewahren. Wieder zurück zu Deinem Beispiel: Warum fängt der Spieler ausgerechnet mit EC an? Gruß elementaar PS.: Mal abgesehen von EC - es ist ja ohne weiteres denkbar, 12/37 spielt bspw. maximal 6 Sätze auf Gewinnziel +2 (Chance >0,5), klappt das nicht, betrachtet er seinen Saldo und entscheidet danach, welche Chancengröße für ein angepaßtes Gewinnziel am besten geeignet ist.

Hallo @Hans Dampf, Praktisch spricht nichts dagegen - und ist sogar empfehlenswert, wenn man ein "Stück" als kleinste Einheit begreift. In Wirklichkeit besteht 1 Stück bei EC natürlich aus 18 Untereinheiten und demzufolge Dutzend/Kolonne bei gleichem Wert aus lediglich 12 Untereinheiten. Aber das braucht einen bei obiger Sichtweise ja nicht weiter zu bekümmern. Gruß elementaar

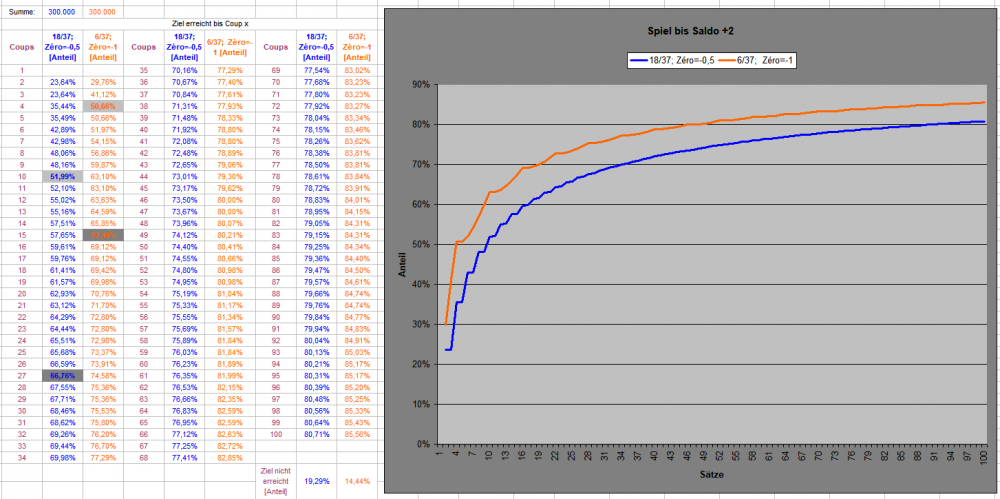
Hallo @Hans Dampf, noch etwas schneller (und am Ende erfolgreicher) sind Transversale Simple. Schneller leider nur bis Coup 4, das läßt dann schnell nach... Die Hälfte und zwei Drittel der erfolgreichen Partien sind markiert. Danke für den Vorschlag! Hat mir Spaß gemacht. Gruß elementaar