elementaar

Hallo @Hans Dampf, lustiger Vorschlag. Kann ich machen. Versuchsbedingungen: 6 Spieler Dutzend/Kolonne 1, 2, 3 gegen 6 Spieler Rot, Schwarz, Impair, Pair, Manque, Passe Alle Gleichsatz, Spielstopp bei Saldo +2 oder nach 100 Coups. Ergebnis in einer Tabelle mit halber zu drittel Chance zusammengefaßt und gegenüber gestellt. Wenn Du so damit einverstanden bist, kann ich das heute Nachmittag machen - ansonsten bitte Änderungswünsche. Gruß elementaar

Hallo @sachse, Diese Frage hat mich, ausgerechnet von Dir gestellt, nun doch einigermaßen verblüfft. Habe ich, auch nur in einem einzigen meiner nun auch schon über 500 Beiträge (erschreckend!), jemals den Eindruck erweckt, mir ginge es dabei um finanzielle Erträge? Du liebe Zeit! Erfreuliche Erträge im Roulette habe ich über 20 Jahre im Landcasino gemacht - mit ballistischem Spiel. Daß es noch andere Dinge gibt, die ganz wesentlich interessanter und beglückender sind, sollte Dir doch nicht ganz verborgen geblieben sein, selbst wenn Du sie für Dich persönlich ablehnst. Für mich sind das z. B. der Erwerb von Fertigkeiten und Erkenntnissen und deren praktische Anwendung. Mein Wissensdurst ist kaum stillbar, und es ist, für mich, kaum etwas befriedigender als eine Aufgabe im Bewußtsein meiner erworbenen Fertigkeiten nach handwerklichen Standards möglichst gut zu lösen. In diesem Forum ist es das Sichtbarmachen von Zufallsgeschehen, nichts weiter. Wenn ich dann im praktischen Spiel ein paar Hunderter, manchmal auch ein paar Tausender mache, wirklich: du liebe Zeit, dann ist das zwar schöner, als wenn es andersherum wäre, aber doch lediglich Folge meines Spiels und nicht sein Grund. Da wäre ich ja, selbst nach meinen Maßstäben, vollkommen bekloppt. Falls Du irrigerweise den Eindruck gewannst, daß sei mein Leben, kann ich nur versichern: das ist nicht so. Nennst Du mich deshalb einen Lügner, werde ich damit leben müssen - schade, aber ich bin ganz guter Hoffnung, daß mir dies gelingen wird. Gruß elementaar

Die Spinnereien der Forensoftware in den letzten ca. 10 Tagen (Zwangsabmeldung nach ein paar Sekunden, nichts hochladen können, ganz neu: unter dem Feld "Antworten" vergangene Beiträge der Seite wieder anzeigen, dafür kein "Dateien hochladen"-Link mehr) und vor allem, daß es scheinbar nicht besser wird, gehen mir so auf die Nerven, daß ich mal Pause mache, so ist das einfach zu zeitaufwendig.

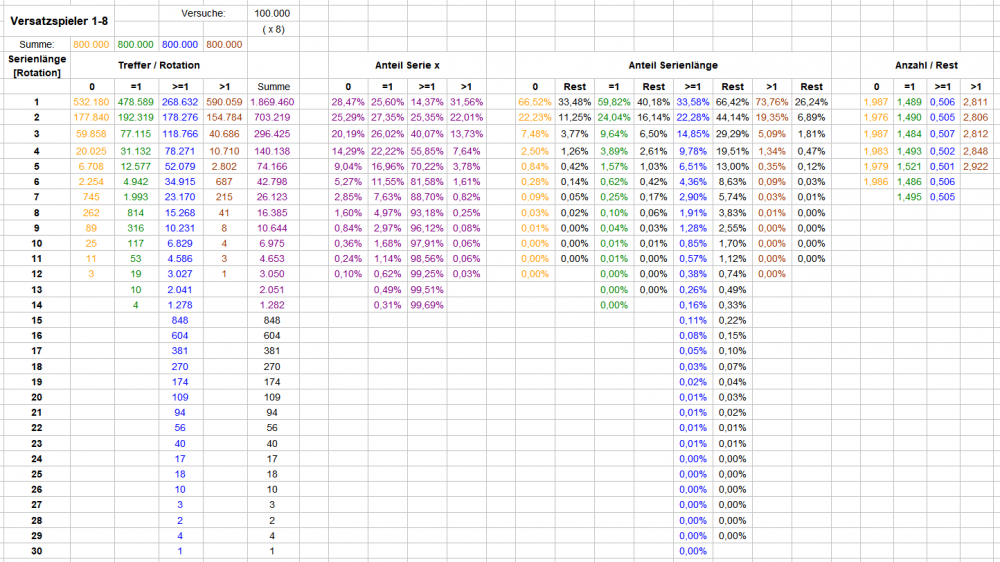
Serienbildung der Versatz- (Satzstufen-) Spieler Betrachtet werden vollständige Rotationen, d.h. alle 8 Coups wird abgefragt, wieviele Treffer die zeitgleichen Versatzspieler in dieser Rotation erzielten. Ich habe vier verschiedene Gruppen gebildet: 0 in der Rotation hat ein Spieler 0 Treffer erzielt. Jeder Treffer in der folgenden Rotation beendet die Serie. =1 in der Rotation hat ein Spieler genau 1 Treffer erzielt. Jede 0-Treffer- wie auch jede >1-Treffer-Rotation, die folgt, beendet die Serie. >=1 in der Rotation hat ein Spieler 1 oder mehr Treffer erzielt. Jede 0-Treffer-Rotation, die folgt, beendet die Serie. >1 in der Rotation hat ein Spieler mehr als 1 Treffer erzielt. Jede 0-Treffer- wie auch jede 1-Treffer-Rotation, die folgt, beendet die Serie. Es wurden ausschließlich abgeschlossene Serien gezählt, d.h. eine 3er-Serie bedeutet, 3 Rotationen hintereinander geschah etwas in der Gruppe Bezeichnetes, in der nächsten Rotation geschah etwas anderes, die Serie bricht ab. Weder werden mit einer 3er-Serie 3 1er-Serien mitgezählt, noch bricht irgendeine Serie mangels Permanenzzahlen ab. Dazu habe ich eine Permanenzstrecke von 50 Rotationen eingerichtet und für jeden Spieler jeweils nur seine erste Serie gezählt. Die längste Serie war 30 Rotationen lang, was ausweislich der Summe "800.000" in den Spaltenköpfen auch stimmt (keine "fehlende" Serie > Länge 50). Wie immer Verfahren "Wenke". Lesebeispiele: Abgeschlossene 3 Rotationen mit 0 Treffern hintereinander wurden 59.858 mal und damit mit 7,48% aller 0-Treffer-Serien gezählt. Abgeschlossene 4 Rotationen mit genau 1 Treffer hintereinander wurden 31.132 mal und damit mit 3,89% aller genau 1-Treffer-Serien gezählt. Abgeschlossene 1er-Serien wurden für alle Gruppen 1.869.460 mal gezählt. Der Anteil von >1-Treffer-Rotationen an allen 1er-Serien beträgt mithin 31,56%. Wer mit diesem Thema, https://www.roulette-forum.de/topic/17866-die-lästigen-intermittenzketten/ und den darin entwickelten Gedanken etwas anzufangen weiß, findet in der ">1"-Spalte ähnliche Verhältnisse zwischen Anzahl und dem jeweiligen Rest wie bei EC. Gruß elementaar

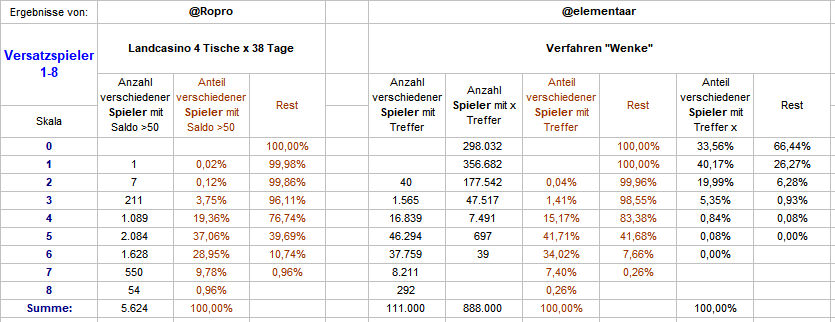
Hallo @Ropro, vielen Dank für Deine Erläuterungen! Ich habe mal eine Gegenüber- und Zusammenstellung unserer beiden Ergebnisse gemacht. Bedenkt man, daß Du zum Erreichen des Partieziels mindestens 2 Treffer benötigst, und ich mit der Zeitbeschränkung einer Rotation lediglich die darin auftretenden Treffer zähle, finde ich beide Zahlenwerke durchaus plausibel und auch kongruent. Es ist ja klar, daß Deine Quoten, von oben nach unten gelesen, etwas niedriger sein müssen - Du hast es ja auch schwerer (mit mindestens 2 Treffern); Anzahl "6" und "7" weichen allerdings ab. Gruß elementaar

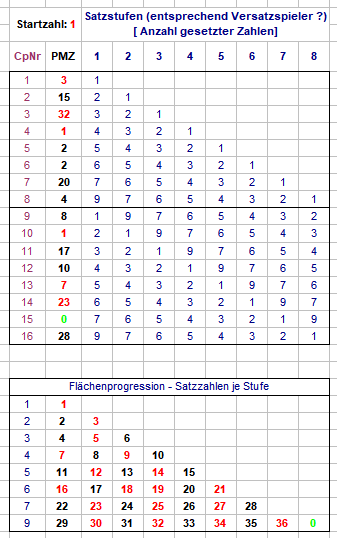
Hallo @Ropro, danke für Deine Antworten! Nur noch mal zur Vergewisserung: Satzstufe bedeutet bei Dir, was bei mir die Versatzspieler sind? Also, bei identischer Startzahl etwa so: Und Du zählst von Tagesbeginn an? Was heißt, daß Satzstufe (Versatzspieler?) 8 pro Startzahl immer 7 Coups weniger spielt als Satzstufe 1? In Deiner Zusammenstellung dann die Anzahl das Partieziel erreichender Satzstufen (Versatzspieler?). Gruß elementaar

Hallo @Ropro, ganz und gar kein Grund für "sorry". Zunächst einmal vielen Dank für Deine Zusammenstellung. Es ist doch äußerst wünschenswert, wenn aus unterschiedlichen Betrachtungsweisen die unterschiedlichsten Ergebnisse hier veröffentlicht werden. Sonst hätten wir doch gar nichts zu besprechen. Zu Deiner Zusammenstellung zwei Fragen: 1. Lesebeispiel: Bei Startzahl "32" lese ich das Vorkommen "60" in der Zeile bezeichnet mit "5", Du schreibst "4", also gezählt mit 1 minus? Das kann aber eigentlich nicht sein, denn Startzahl "35" verzeichnet das Vorkommen "1" in Zeile "1", das wäre dann mit 1 minus Satzstufe "0". 2. Welche Zählung ist überhaupt abgebildet? Sind das Anzahlen unterschiedlicher treffender Satzstufen (die Dauer der Partie wird nicht abgebildet), die dann zum Erreichen des Partieziels führen? Die Anzahlen unterschiedlich gesetzter Satzstufen werden es wohl nicht sein. Gruß elementaar

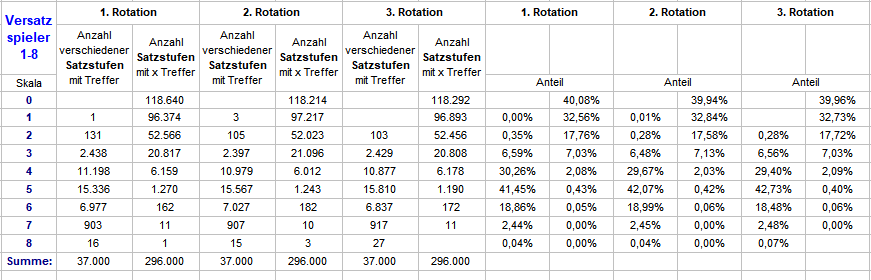
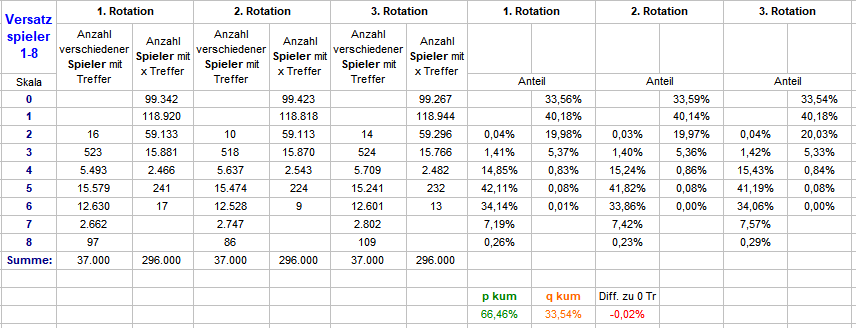
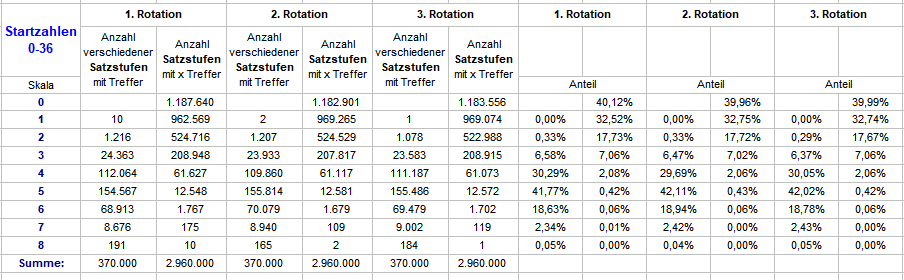
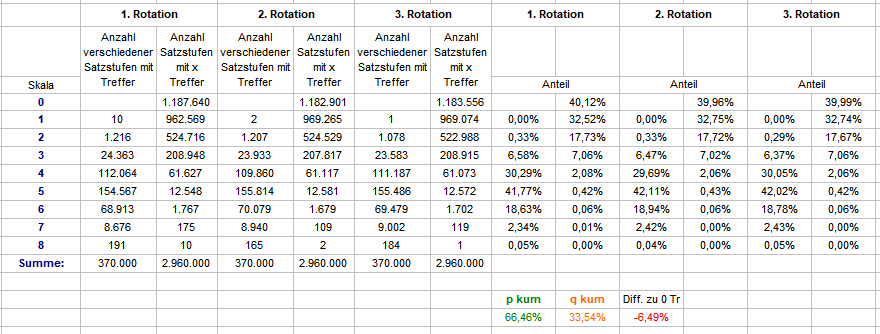
Kaum bringt es @Albatros (Danke!) zur Sprache, schon ist es passiert: Achtung: Korrektur - Fehler in der Tabellenbeschriftung! Beim Überlegen über eine Falsifizierungsmethode für obige Ergebnisse ist mir ein dicker FEHLER bei der Beschriftung der Spaltenköpfe aufgefallen. Bei "Anzahl der ..." muß es statt falsch: "Spieler" richtig: "Satzstufen" heißen, ganz wie in der Tabelle der 37 Startzahlen. Daß das etwas komplett anderes ist, darauf deuten die ziemlich unterschiedlichen Wörter schon hin. Es tut mir sehr leid - eine heftige Schlampigkeit, die eigentlich nicht passieren sollte. Das sind so die Momente, wo ich mit Überzeugung denke: "Laß es doch am Besten gleich ganz bleiben, Du siehst doch, daß Du zu doof für Alles bist..." Die Werte ändern sich nicht, die Schlußfolgerungen aber sehr wohl. Auch die Differenzrechnung ist für "Satzstufen" natürlich nicht statthaft. Leider kann ich die FALSCH beschriftete Tabelle oben nicht mehr ändern, am Besten in den Orkus mit ihr, hier die beiden neuen (Satzstufen UND Spieler): Wie zu sehen, bei "Spieler" gibt es keine erwähnenswerte Differenz, die "Satzstufen" richten sich nach ihrer jeweiligen Trefferwahrscheinlichkeit, deshalb ist ein Vergleich mit der kumulierten Trefferwahrscheinlichkeit aller Satzstufen einer Rotation unsinnig und falsch. Hier auch noch die Tabelle der Startzahlen ohne Differenzrechnung. Wenigstens war meine Skepsis mit der, hilfsweisen, Erklärung berechtigt: wenn es (dauerhaft) nichts bringt, nach dem immer gleichen Prinzip Favoriten zu verfolgen, dann kann auch das Ausscheiden derselben auf Dauer nichts bringen. Gruß elementaar

Hallo @Albatros, Wir versuchen zu ergründen, wie sich eine Flächenprogression, in der in insgesamt acht Satzcoups alle 37 möglichen Zahlen genau einmal gesetzt werden, verhält. Ich verstehe das als Grundlagenforschung. Zugleich, und für mich nicht unwillkommen nebenbei, mag es als Akt aktiven Widerstands (wenn Du das aufgeplusterte Wort verzeihst) in einem Rouletteforum dienen. Dank Corona und der dadurch bis zur Geisteskrankheit vernebelten Hirne geht ja morgen, spätestens übermorgen die Welt unter. Nach alter Weisheit muß man dann heute einen Apfelbaum pflanzen. Es ist einfach schön zu sehen, daß wenigstens beim Roulettespiel die grundlegendsten handwerklichen Regeln der Statistik immer noch gelten - anders als scheinbar im Rest der Menschenwelt. Schade übrigens, daß Du keine Belege für Deinen Eindruck, hier seien "hospitalisierte Hunde" am Werk, bringst - das hätte erheiternd und/oder erhellend sein können. Die Versuche, sich selbst in den Schwanz zu beißen, habe ich schon vor Jahren mangels ausreichender Gelenkigkeit eingestellt - im übertragenen Sinn ist dieser Zeitvertreib leider nie ganz auszuschließen. Gruß elementaar

Hallo @Hans Dampf, Dein Einwand ist vollkommen berechtigt, mit der kleinen Korrektur, daß die anderen (oder der achte Satz) dann etwas weniger als -1 einfahren (die Trefferanzahl insgesamt bleibt ja gleich und verteilt sich auf ca. 6,5% weniger Spieler). Ich habe aber den Zustand des freudigen Erstaunens (solche Abweichungen mit einer derart einfachen Spielanlage! - das sieht man selten), aber auch der Skepsis, noch nicht verlassen, und suche eher nach Möglichkeiten, die Ergebnisse mit einer anderen Methode zu falsifizieren und halbwegs verlässliche Sollwerte für die Mehrtreffer-Spieler zu bekommen. Was man damit anfängt - für diese Frage bin ich noch zu paralysiert. Immerhin scheint die alte Forderung nach dem "Mehr verlieren als man sollte" deutlich erfüllt, und das als Ergebnis einfachen und vollkommen logischen Denkens. Da ist Dir ein genialer Streich gelungen - vielmals herzlichen Dank! Danke, Dir auch, aber so richtig! Gruß elementaar

Hallo @Ropro, Ja - Treffer und NichtTreffer, das Sandardverfahren mit weit überwiegenden Vorteilen. Da ja immer (Spieler)rotationen verglichen werden, ist der Umsatz immer 37 Stück, Sollminus ist -1, jeder Treffer erhält 36 Stück Auszahlung. Ein Saldoverlauf, auch innerhalb einer Rotation, ist nicht ableitbar. Die Abweichung bei den Gar-nicht-Treffenden Spielern (der einzigen Gruppe, zu der ein errechneter Sollwert vorliegt) von ca. 6,5% ist deshalb so erstaunlich, weil mir außer den fehlenden Mehrfachtreffern einer Sequenz nichts zur Begründung einfällt. Vor Jahren hat @Hans Dampf so lapidar wie zutreffend bemerkt (sinngemäß) "ohne Wiederholer innerhalb einer Rotation kann man nach Coup 1, mit Tronc nach Coup 2, nicht mehr verlieren." Ich habe das damals mit Vergnügen an dem logischen Gedankenspiel gelesen, mehr aber auch nicht. Weder bin ich auf die Idee gekommen, ein entsprechendes Spiel zu konstruieren, noch hätte ich vermutet, daß es dann eine solche Kraft entfaltet (kolossale Fehleinschätzung). Ich sollte nicht der erste sein, der demütig feststellt, der Typ ist deutlich schlauer als ich. Wie gut, daß er hier im Forum mitmacht! Leider sind meine ohnehin rudimentären Rechenfähigkeiten viel zu limitiert, um die Sollwerte für die 1 bis mehrfach treffenden Spieler zum Vergleich auszurechnen. Am ehesten sollte es noch bei 37 Startzahlen und festen Stufen für alle gelingen (multinomial), Vertrauen hätte ich in meine Rechenergebnisse allerdings nicht. Ich krame mal im Archiv, ob ich entsprechende Auszählungsergebnisse habe. Gruß elementaar

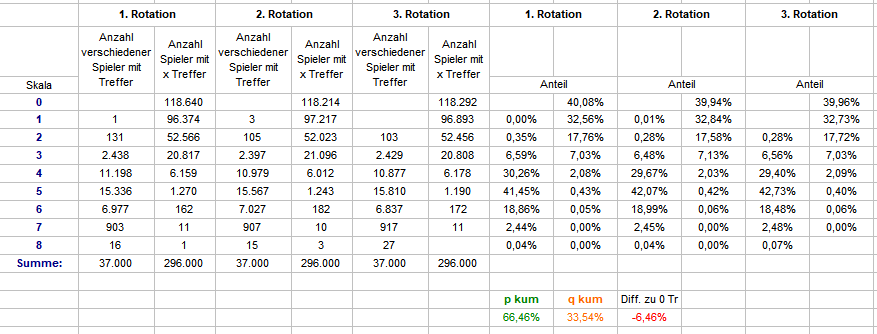
Nun habe ich, analog zu oben, alle 37 Startzahlen, aber mit feststehenden Stufen der Flächenprogression geprüft. In arithmetischer Reihe die Startzahlen 0-36. Jede dieser Startzahlen spielt die Stufenreihenfolge mit 1, 2, 3, 4, 5, 6, 7 und 9 Zahlen. Jede Startzahl beginnt mit Stufe 1, zeitgleiche Abfrage aller 37 Startzahlen über drei aufeinander folgende Rotationen. Gefragt habe ich jetzt natürlich nach der Häufigkeit verschiedener Satzstufen innerhalb einer Rotation und der Trefferanzahl in den Satzstufen. Wie zu sehen, unterscheiden sich die Ergebnisse nur marginal von den obigen. Wenn ich es richtig sehe: Raten wir also entweder die Startzahl oder die beginnende Satzstufe, und spielen eine vollständige Rotation, haben wir eine signifikant erhöhte Chance (+ ca. 6,5%) falsch zu raten, d.h. auf einen Strang zu kommen der keinen Treffer produziert; und das mit einem solch simplen Spielaufbau. Ich muß gestehen, so ganz geheuer ist mir dabei nicht. Ich hätte es nicht für möglich gehalten. Gruß elementaar

Hallo @Ropro, es ist ja sehr gut und hoch willkommen, daß Du nachfragst. Allein die Notwendigkeit, dazu dann erläuternde Texte verfassen zu müssen, erweitert bei mir im Hintergrund die Gedankenwelt. Das schätze ich sehr. Wenn kein Mensch versteht, mit welchen Voraussetzungen die Ergebnisse zu Stande kommen, gibt es auch keine Möglichkeit der Verbesserung und Weiterführung von außen. Dann wäre mein öffentliches Treiben sinnlos. Und Ergebnisse, die sich als irrelevant erweisen, auf den Müll zu werfen, darin dürften wir wohl alle große Übung haben. Keine Tränen darüber. Gruß elementaar

Hallo @Ropro, Richtig. Das verstehe ich nicht. Ich verstehe zwar Deine Erläuterung (8 zeitlich versetzte Startsequenzen x 37 Startzahlen), nicht jedoch, was das mit meinen zuletzt gemachten Untersuchungen zu tun haben könnte. 8 zeitlich versetzte Startsequenzen bedeuten ab Coup 9 eindeutig 8 zeitgleiche Versatzspieler pro Startzahl. Die Versatzspieler und ihr Zusammenspiel lassen sich aber erst vergleichend betrachten, wenn auch alle Spieler mitspielen. Ab diesem Zeitpunkt gibt es bei bei Dir pro Coup genau 8 Treffer, bei mir pro Coup genau einen. Die Kombination mit den 37 Startzahlen habe ich u. a. aus Übersichtsgründen nicht gemacht. Falls sich das Rätsel nun nur mit dieser Kombination erhellen lassen sollte oder es daran liegt, daß in den ersten 8 Coups erst nach und nach alle mitspielen (und möglich ist das ohne Weiteres), bin ich auf dem komplett falschen Dampfer, das ist doch klar. Das habe ich weiter oben aber schon beschrieben. An meinen vorgestellten Ergebnissen (sofern ich richtig habe zählen lassen) ändert das jedoch nichts. Ob dabei meine Ergebnisse in irgendeiner Hinsicht und für Irgendjemanden hilfreich sind, weiß ich natürlich auch nicht, es ist ein Entdeckungsverfahren, dessen Ausgang ich nicht kenne - das behaupte ich aber auch nicht; mir geht es bei meinen Beiträgen zur Zeit ausschließlich um reine Wissensvermehrung, ob und was damit anzufangen sei, kann man sich danach überlegen. Gruß elementaar

Ein weiterer Beleg, daß an diesem Spiel irgendetwas Verrücktes im Gange ist (Dank an @Hans Dampf für die Anregung): wieviele verschiedene Spieler treffen innerhalb von 8 Coups, und wieviele Treffer erzielen sie. Ausgezählt wurden drei aufeinander folgende Rotationen. Man sieht: das Verhalten ist weitgehend synchron. Es gibt aber einen eklatanten Überhang an Spielern, die überhaupt nicht treffen. Die Differenz zum Soll beträgt ca. 6,5%. Überschlagsmäßig: bringt man die 5,4% zur Anrechnung, die man für ein beliebiges Dagegen-Spiel braucht, bleiben immer noch ca. 1,1% Plus übrig. Ich wollte das, wegen der Schwankungen, nicht wirklich spielen, aber immerhin. Und wie paßt dieser Befund zu "nach einer Weile gibt es einen Überhang an Spielern über Normalminus"? Bedenkt man nun außerdem, daß sich ein Plein 2er zu über 55% aus einer der letzten 7 Zahlen bildet, müßte die Quote der lediglich einen Treffer erzielenden Versatzspieler ebenfalls erhöht sein, denn ein Spieler, der eine Zahl getroffen hat, wird dieselbe Zahl innerhalb seiner Sequenz sicher nicht nochmals treffen. Da die Anzahl der zu verteilenden Treffer pro Rotation aber gleich bleibt, kann dies nur bedeuten, daß es mehr Spieler mit >1 Treffern gibt als zu erwarten wäre. Gruß elementaar

Hallo @Ropro, Das ist natürlich schade. Von welcher "oberflächlichen Betrachtung" sprichst Du? Will man gewinnende Frequenzmuster für sich nutzen, benötigt man genügend sichere Indikatoren - das ist, zugegeben, schlicht genug gedacht - aber wie anders könnte ein erfolgreiches Spiel aufgebaut sein, als mit der Lösung der Frage: wie erkenne ich, daß meine nächsten getätigten Sätze überwiegend gewinnen werden? Indikatoren können andere Frequenzmuster, Wendepunkte oder nach Kriterien zusammengestellte Einzelpunkte, die zusammen wieder eine Frequenz darstellen, sein. Es tut mir wirklich leid, daß ich so viele Deiner Fragen mit "weiß ich (noch) nicht" beantworten muß; diese hier ist wieder eine, die ich mit meiner Untersuchung ja abklären will! Sieht man die Sache ähnlich der Trefferfrage für den Dauergewinn (schon der erste Treffer muß schneller, öfter, billiger erscheinen, sonst wird das nichts - deshalb kann man sich ausschließlich auf den ersten Treffer konzentrieren), wäre das zu vermuten. Nach allem, was wir über das Spiel wissen, kann genau das aber nicht sein. Ein einzelner Spieler wird zuverlässig seine -2,7% einfahren und folglich egal welche gedachte Linie mit Treffer oder NichtTreffer schneiden, ganz wie es seine jeweilige Trefferwahrscheinlichkeit vorgibt. Wenn also bei meiner Untersuchung überhaupt etwas Verwertbares heraus kommt, dann müßte das, in meinen Augen, einzig am Zusammenspiel aller 8 Spieler liegen. Der ganze Versuchsaufbau kann aber auch, nicht zu unterschätzen bei diesem Spiel!, eine bloße Folge purer Numerik deutlich machen. Besten Falles hätte man ein (noch unbekanntes aber signifikantes) Frequenzmuster in der Waagerechten mit einem wirksamen Indikator in der Zeitachse. Wie dieses (gewinnträchtige) Zusammenspiel dann genau aussieht, wäre in einem weiteren Schritt zu klären. Gruß elementaar PS: die Versuche der Indizierung in Deinen letzten Beiträgen habe ich übrigens analog zum Geschilderten verstanden, ich hoffe das war nicht falsch.

Hallp @Ropro, Da bin ich überfragt. Die letzten Untersuchungen befassen sich ja lediglich mit einzelnen Punkten. Nehmen wir an, ein beliebiger Spieler hätte in Coup 35 einen Saldo von -28. Normalminus ist zu diesem Zeitpunkt folglich -35. Dieser Spieler hätte im nächsten Coup 9 Stücke zu setzen. Sein Saldo kommt also von oben (auf die Normalminuslinie). Im nächsten Coup hätte er die Möglichkeit Normalminus zu schneiden - wenn er nicht trifft, ist sein Saldo -37, Normalminus -36. Diesen einen Punkt betrachte ich und frage, hat er getroffen - Ergebnis +27 für diesen einen Satz, keine Schneidung - oder hat er nicht getroffen - Ergebnis -9, Schneidung. Das jeweilige Ergebnis wird unter Markierung 3 addiert. Ein anderer Spieler hat vielleicht in Coup 35 einen Saldo von -42 erspielt und im nächsten Satz 1 Stück zu setzen. Seine Saldolinie hat sich von unten so an Normalminus angenähert, daß bei Treffer in Coup 36 eine Schneidung geschehen würde. Trifft er, ist sein Saldo -7 , Soll -36, Schneidung. Trifft er nicht, ist sein Saldo -43, keine Schneidung. Für den nächsten Coup aber direkt wieder Markierung 4, denn er hätte dann 2 Stück zu setzen und hätte bei Treffer immer noch die Möglichkeit Normalminus zu schneiden. Für den einen Satz wird entweder +35 oder -1 addiert. Das alles basiert auf dem (vielleicht zu) banalen Gedanken, wenn wir im Fortgang der Permanenz viel mehr Spielersalden über Normalminus sehen, muß das Schneiden von unten letzten Endes erfolgreicher als erwartbar sein und/oder das Schneiden von oben seltener (weil Treffer an den möglichen Stellen), weil zu häufiges Schneiden von oben ja die Anzahl der Spieler unter Normalminus erhöhen würde. An der naheliegenden Frage, wenn ein oder mehrere Spieler möglicherweise schneiden, was machen währenddessen die anderen (also das in Beziehung zueinander setzen), bin ich noch längst nicht, denn es hängt ja letztlich daran, wieviele Versuche braucht ein von unten kommender Spieler bis seine Schneidung vollzogen ist. Gibt es an diesen einzelnen Punkten nichts Bemerkenswertes, könnte man noch ein Überlagerungsspiel in Erwägung ziehen, für Gleichsatz wäre dann aber erwiesen, daß diese Punkte nichts gewinnträchtiges in sich tragen. Die bisherigen Ergebnisse scheinen darauf hinzudeuten, daß an dem simplen Gedanken etwas dran ist. Würden sich die Ergebnisse bei Parallelverschiebungslinien den erwartbaren -2,7% annähern, könnte man bei zeitgleicher Betrachtung bestimmte Sätze ausschließen. Gruß elementaar

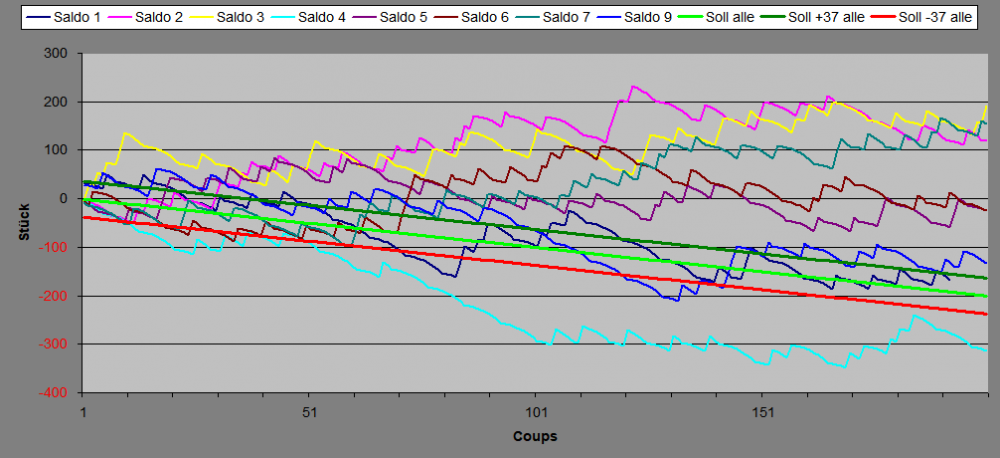
Hallp @Ropro, Gern. Im Schaubild habe ich eine Parallelverschiebung von Normalminus (Graph "Soll alle") je einmal mit + und - 37 (Stück) vorgenommen. Dies bewirkt in der Plusverschiebung, daß mehr Spieler von unten schneiden können, in der Minusverschiebung, daß mehr Spieler von oben schneiden können (wenigstens als Hypothese). Denkbar ist nun zum einen, daß sich durch geschickte Wahl der Verschiebung die Vorlauffrage selbst erledigt. Außerdem, je nachdem, wie sich dadurch die Verhältnisse zwischen potentiellen von-oben- zu von-unten-Schneidern ändern (Daten liegen ja noch nicht vor) könnten sich, mitsamt der dazugehörigen Umsatzprozentergebnisse, bei den einzelnen Spielern Saldoperioden (Frequenzen) fassbarer abzeichnen, die Deiner Beobachtung von 37-74 Coups entsprechen. Das "T"-Wort verwende ich hier mal nicht. Es ist bloß öffentliches Spekulieren und die Schilderung, welche neuen Erkenntnisse wir im besten Fall gewinnen könnten. Gruß elementaar

Hallp @Ropro, danke für die Rückmeldung! Es spricht nichts dagegen, das Normalminus für jeden Spieler umsatzgenau abzubilden. Das ergibt dann für jeden Einzelnen den weiter oben kurz diskutierten Zackengraphen, der sich mit denen aller Spieler je 8 Coups in der Ganzzahl vereint. Ich will damit aber noch warten, bis (falls) ich noch bessere Ergebnisse erhalte. Bisher sind es ja eher Befunde im Negativen: es scheint einen Effekt zu geben, der aber nur so stark ist, daß sich die Verlustrate verkleinert. Klar, ohne Hausvorteil sollte sich ein kleines Plus abbilden, aber die Schwankungen wären enorm. Zwei Varianten habe ich noch vorher auf dem Zettel; beide hängen mit der zur Frage "Wieviele Spieler sind wann über Normalminus" gefundenen (Halb-)Parabelkurve zusammen. - Gibt es ein optimales Zeitfenster für Vorlauf und Satzphase? Wobei parabelentsprechend, höchste Steigung im Ursprung, wegen unsinniger Ergebnisse leider ausscheidet. Es könnte sein, daß es sich geradezu umgekehrt verhält: flachere Steigung ergibt "sicherere" Schneidung. Da muß ich die damaligen Ergebnisse noch einmal studieren. - Was ist denn, wenn man Normalminus (als sowieso virtuelle Linie) parallelverschiebt, beispielsweise + oder - 10 Stück ö.ä. Damit könnte man nebenbei auch näherungsweise (über die Anzahl der Spieler, die sich dann über/unter diesen Graphen befinden) Belege für Deine Beobachtung der 37-74 Coups Perioden finden. Gruß elementaar

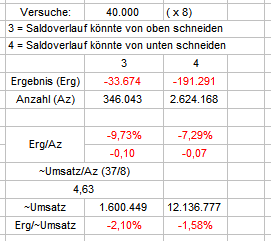
Ein neuer Ansatz von zunächst geringer Komplexität geht so: Betrachtet werden insgesamt 48 Coups (6 Rotationen). Die ersten 8 Coups dienen als Vorlauf. Danach werden die 8 Spielersaldenverläufe jeweils Coup für Coup danach abgefragt, ob sie im nächsten Coup Normalminus schneiden könnten, und wenn ja, wie das Ergebnis ist. Dabei wird unterschieden, ob sich der Spielergraph von oben annähert (Markierung 3), oder ob er von unten kommt (Markierung 4). Der von oben kommende Spielersaldoverlauf würde dabei mit einem Treffer im nächsten Coup die Schneidung vermeiden, der von unten kommende mit einem Treffer die Schneidung vollziehen und damit über Normalminus kommen. Nach der viel weiter oben gezeigten, verblüffenden Feststellung, daß sich nach einer Weile viel mehr Spieler, als man erwarten würde, über Normalminus befinden, sollten die von unten kommenden Spielergraphen deutlich besser abschneiden. Mal sehen, ob diese Annahme stimmt: hier die Ergebnisse für 40.000 (x 8 Spieler x 40 Coups) Versuche: Da ich zwar die Ergebnisse in Stück, die 3er und 4er Markierungen aber nur per Anzahl gezählt habe, kann ich den getätigten Umsatz mit 37/8=4,63 nur schätzen, durch die Vielzahl der Versuche sollte das allerdings ganz gut hinkommen. Das stark unterschiedliche Aufkommen von 3 und 4 erklärt sich überwiegend aus dem Umstand, daß der von oben kommende Graph bis auf 1-9 Stück an Normalminus herankommen muß (seinen nächsten Einsatz nämlich), damit es zur eventuellen Schneidung kommen kann, während dem von unten ansteigenden Graphen 1-34 Stücke für die Annäherung zur Verfügung stehen (nämlich jeder Treffer - Einsatz). Schneidet also ein 3er tatsächlich (d.h. verliert er seinen Einsatz), steht für den nächsten Coup sofort eine 4 auf seinem Zettel, andersherum ist das nicht in jedem Fall so. Gruß elementaar

Hier sind die Ergebnisse für 100.000 (x 8) Versuche: Im Vergleich zur kürzeren Versuchsstrecke oben, sehen wir eine sehr langsame Annäherung an den Sollwert. Daraus ergibt sich die spekulative Teilantwort auf @Ropros Frage: Es könnte sich rentieren, qualifizierte Schneidepunkte jeweils in Reihe zu betrachten und entsprechend der letzten jeweiligen Folgen zu spielen. Wobei da noch ein Wort zur Qualität der Auszählung fällig wird: Die Natur der Markierung mit -1, 0, 1 mag eine Eindeutigkeit suggerieren, die im Falle der 0-Markierung aber bloß numerisch ist: Spielersaldo und Normalminus stimmen an einer Coupstelle genau überein - nicht mehr und nicht weniger ist damit ausgesagt. Sehr leicht denkbar ist ein Saldograph, der, aus einer Richtung kommend, auf Normalminus trifft, numerisch exakt gleich ist und damit mit 0 markiert wird, und sich dann in dieselbe Richtung wieder davon macht. In diesem Fall wäre das Wort "Berührung" richtiger als "Schneidung". Erst das mehrfache Auftreten von "0" deutet somit auf einen Aufenthaltsort des Spielersaldos, innerhalb der letzten 24 Coups, in der Nähe von Normalminus hin (+- 37 Stück). In den Spalten (wo die letzten 8 Coups abgebildet sind) kann man hingegen sehen, daß es Schneidungen gibt, die nicht mit 0 markiert werden. Dabei sind die Summen 8 und -8 eindeutig (keine Schneidung), die mit 6 und -6 mit einer Schneidung, die dazwischen mit mindestens einer Schneidung, man weiß jedoch leider nicht wieviele genau. Die gemachte Untersuchung beantwortet die gestellte Frage "Spielen Schneidungen eine Rolle?" somit zwar eindeutig, jedoch leider nur unvollständig. So ist das halt mit zu leistungsschwachen Gehirnen: die Probleme, die "0" als Markierung in sich trägt, habe ich @Egoist gegenüber schon mal geschildert, und freue mich dennoch an der Einfachheit von -1 und 1, leider nur solange, bis man mehr wissen will. Meine Arbeitshypothese ist ja immer: "spielt alles keine Rolle", und solange sich diese These bestätigt, ist es auch egal ob man von -1 über 0 zu 1 geht; findet man jedoch scheinbar doch etwas, werden weitere, anders aufgebaute Versuche nötig, warum also nicht gleich richtig? Ein ewiges Rätsel der Bequemlichkeit. Gruß elementaar

Das weiß ich natürlich noch nicht. Als ich mir die 40 Coups Vorlauf unter der Fragestellung betrachtete, wie kann man das Geschehen normierend vereinfachen, fielen mir halt wieder die Schnittpunkte auf. Also entschloß ich mich, zunächst einmal zu prüfen, ob sie überhaupt eine praktische Rolle spielen, oder man sie ganz einfach ignorieren kann. Das scheint nicht so zu sein. Gruß elementaar

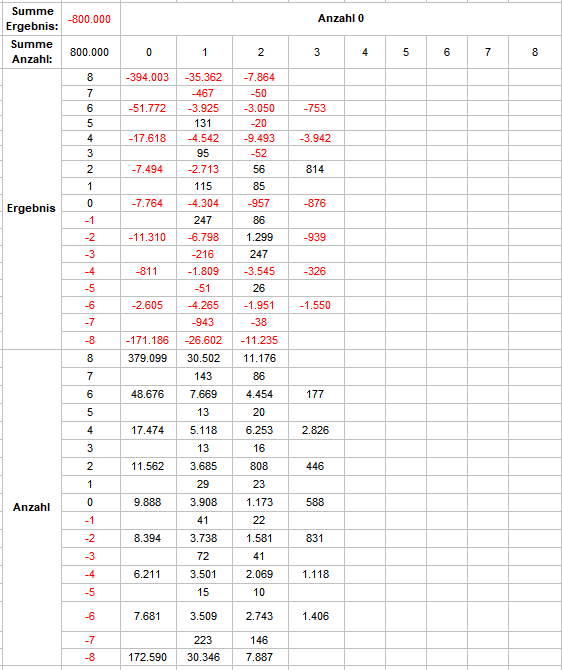
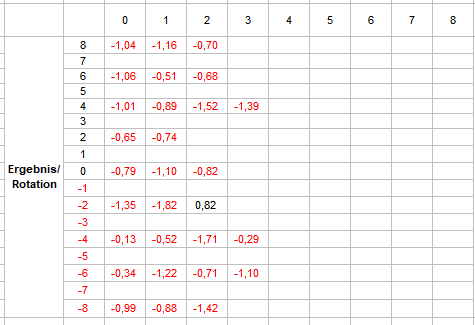
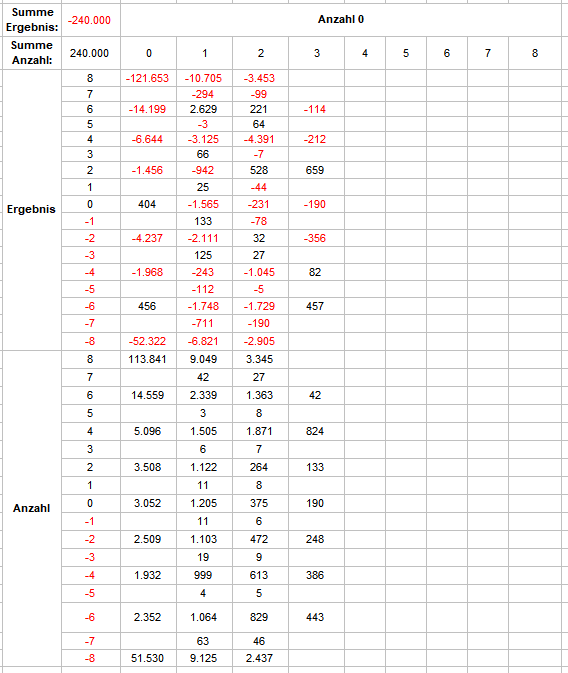
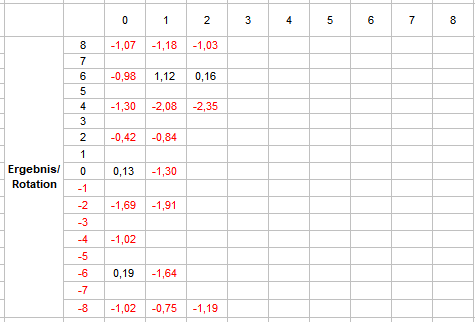
Nach den ganzen langweiligen Standardabfragen, habe ich mir mal wieder etwas potentiell Aufregenderes gegönnt. Im Vergleich zum Normalminusgraphen versuche ich möglicherweise gewinnenden Frequenzen auf die Spur zu kommen. Daß dies alles andere als leicht ist, sollte selbsterklärend sein: je länger die Vorlaufstrecke, desto explosionsartiger nehmen die Möglichkeiten zu. Man muß also eine irrsinnige Anzahl an Versuchen machen, um überhaupt über eventuelle Muster spekulieren zu können. Zur Zeit scheint mir das Vereinfachen der Aufgabestellung immer noch als der praktikablere Weg. Als erstes möchte ich wissen, ob das Schneiden der Saldoverläufe mit Normalminus im Vorlauf irgendeinen Einfluß auf das dann erspielte Ergebnis hat. Eingerichtet habe ich mir dazu Folgendes: Alle acht Versatzspieler werden zeitgleich betrachtet. Vorlauf 40 Coups (5 Rotationen), danach 8 Coups (1 Rotation) als gespielt angenommen. Die Normalminuskurve fällt stetig um ein Stück/Coup. Jede Saldoverlaufskurve wird mit der bekannten Markierung (-1 für kleiner, 0 für gleich, 1 für größer) ausgezeichnet. Für die letzten 24 Coups (3 Rotationen) vor Spielbeginn wird nun gezählt, wie oft eine Schneidung (=0-Markierung) stattfand. Dies wird in Beziehung gesetzt zur simplen Addition der letzten 8 Markierungen (1 Rotation) vor Spielbeginn. Ein Pärchen 1-8 bedeutet also: die letzten 8 Coups befand sich der Saldo des Versatzspielers über Normalminus und es gab in den letzten 24 Coups eine Schneidung. Ich werde die Stichprobe auf jeden Fall noch vergrößern, ein vielversprechender Vorbericht über 30.000 (x 8) Versuche, ergibt dieses Ergebnis: Lesebeispiel: Das Pärchen 0-8 erschien 113.841 mal und produzierte dabei ein Ergebnis von -121.653 Stück. Was das soll, macht vielleicht diese Weiterverarbeitung deutlicher: Hier habe ich die Anzahl der jeweiligen Ereignisse durch das jeweilige Ergebnis geteilt (Sollwert = -1). Damit das nicht zu unübersichtlich und sinnlos wird, sind nur die Positionen abgebildet, die mindestens 1.000 Ereignisse vorweisen konnten. Man unterschätze dabei nicht die Kraft der Nachkommastellen: die -1,07 für das Pärchen 0-8 bedeuten eine 7%ige Abweichung. Stand jetzt würde ich mich soweit vorwagen und behaupten die Schneidungen spielen eine Rolle. Gruß elementaar

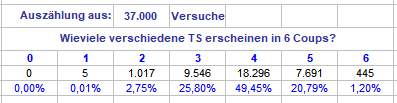
Hallo @Hans Dampf, ob diese Überlegung wirklich richtig ist? Eine Uraltauszählung (die hoffentlich stimmt): weist für 6 Coups und 6 verschiedene TS 1,20% aus, die obige Normalo-Auszählung für 8 verschiedene Treffer-Spieler in 8 Coups 0,28% Erhöhe ich die Anzahl der Mitspieler sollten, nach meinem Verständnis, die Quoten sinken, bis hin zu 37 treffenden Einzelzahlspielern in 37 Coups mit 0,fantastilliarden%. Oder meinst Du etwas ganz Anderes? Gruß elementaar

Hallo @Ropro, vielen Dank für Deine erläuternden Worte. Unsere Vorstellungen haben durchaus ähnliche Blickrichtungen - skeptisch (ohne es zu wissen) sehe ich allerdings die von Dir erhofften Betrachtungsdistanzen. 2-3 Coups zur Satzbestimmung sind schon sehr nahe dran am Vorher-Nachher-Coup. Wenn das gelänge, wäre es natürlich traumhaft, und mein Einwand soll auch keinesfalls demotivierend wirken. Denn aus meiner Sicht geben die bisher betrachteten Verlaufskurven das zwar nicht her, als Betrachtungsdistanz zur Satzbestimmung würde ich eher 5-10 Rotationen vermuten. Diese bloße Vermutung basiert allerdings auf der ausschließlichen Betrachtung der acht Verschiebungsspieler, bei Dir kommen ja noch die 37 Startzahlen hinzu. Rechnerisch (max 80 Betrachtungscoups / 37 Startzahlen = 2,xx Coups) also mit Dir übereinstimmend - aber ob eine solche Komprimierung der relevanten Informationen wirklich gelingen kann? Insofern weiß ich auf Deine Frage noch keine Antwort; so weit bin ich noch nicht. Es ist dabei durchaus möglich, daß die Komprimierung das Erkennen des Relevanten sogar befördert, dann sitze ich mit meiner Schritt-für-Schritt-Methode noch nächstes Jahr dran. Klar ist jedoch, wenn die Sätze einmal bestimmt sind, muß sehr schnell getroffen werden - länger als 1 bis höchstens 2 Rotationen (8-16 Satzcoups), besser noch deutlich kürzer, darf man sich nicht damit aufhalten. Das ist allein schon ein Gebot der Statistik (und der auftretenden Schwankungen). Gruß elementaar