elementaar

Hallo FavRad, Oh ja, wenn auch mit deutlich größerer Datenbasis. Der Vergleich zeigt, leider, nichts worauf ich sofort anspringen würde (Irrtum aber nicht ausgeschlossen, ich bin im Moment an etwas ganz anderem dran, und deshalb zur Zeit nicht der kompetenteste Gesprächspartner). Und in der Datenbasis sehe ich auch das größte Manko bei einer solchen Untersuchung mit Landcasinozahlen (neben prinzipiellen, von denen ich einige weiter oben angesprochen habe). Die Gründe für die "künstlichen" Zahlen ( vertrauenswürdiger RND plus "Wenke") habe ich ja schon dargelegt. Wenn man nun auf handgeworfene Landcasinozahlen besteht, ist das zunächst ja nur eine Frage der Art des Zahlengenerators, der die Zufallszahlen produziert (und nebenbei der Zuverlässigkeit der Angaben der Landcasinos oder der eigenen Mitschrift). Man könnte diese Zahlen natürlich auch dem Verfahren "Wenke" unterziehen, und damit mit relativ überschaubarer Gesamtzahlenmenge eine SEHR große Anzahl frischer Permanenzen erzeugen. Wenn man nun aber außerdem darauf besteht, die Landcasinozahlen müßten chronologisch behandelt werden, vervielfachen sich die Probleme. Zunächst: woher nehmen? Für einen statistischen Nachweis bei EZ braucht man gemeinhin Unmengen an Zahlen. Dann die Frage nach der Ballistik: Damit Kessel, Kugel, Croupier, Mitspieler keine Rolle spielen (sofort mein Einhaken: warum sollte man das wollen?, das ist, meiner Ansicht nach, doch der größte Spielervorteil im Landcasino), verurteilt man sich zusätzlich zu sehr großen Zahlenmengen (damit sich die genannten Effekte ausgleichen). Und dann taucht, zum Beispiel und so nebenbei, die Frage der Douplettenhäufigkeit der Fx bei EZ auf. Nur mal vorgestellt, man käme da zu einem vielversprechenden Befund, wie könnte man genügend sicher sein, nicht doch einem Aufzeichnungs- und/oder Kesselfehler u.ä. aufzusitzen. Mir scheint es deutlich erfolgversprechender zu sein, sich die real spielbaren Permanenzverläufe anzuschauen (denkbar wäre es auch, für jedem Croupier dessen jeweils eigene Permanenz fortzuschreiben; das muß, glaube ich, gar nicht weiter erläutert werden...). Ropro hat in Sachen Verlauf hier einen sehr guten, sogar illustrierten, Hinweis gegeben: https://www.roulette-forum.de/topic/18315-permanenzen-lesen-und-beurteilen/?tab=comments#comment-378834 Ich habe Deinen Ansatz als sehr ähnlich verstanden. Falls Du in Blatt 1 etwas findest, bietet es sich an, nachzuschauen, wie die betreffende Stelle in den anderen Blättern (jeweils 1 Coup Versatz) aussieht. Obwohl bloß bis Cp 10 gehend, kann man da schon etwas feststellen. Viel Erfolg! Gruß elementaar

Hallo Ropro, in den Spalten B:S stehen die Trefferwerte in absoluten Coups (wie in der alten Tabelle), neu hinzugekommen sind die Spalten U:AL. Hier sind die relativen Coupswerte verzeichnet (also bspw. nach dem 1. 2er dauerte es x Coups bis der 1. 3er erschien (wie in dem Ausriss viel weiter oben). Für manche Fragen geht damit das analysieren schneller. Ich würde empfehlen beide Tabellenteile nach dem download wieder zu einer zu vereinigen. Gruß elementaar

Hallo Ropro, was siehst Du denn doppelt? Oder stehe ich auf der Leitung? Gruß elementaar

Teil 2 (Beginn mit Cp 6 bis 10): EZ_FavRad_Wann_erscheint_1.02er_bis_1.10er_TrAbstände_Daten_06-10.xls Grußelementaar

Hallo FavRad, hallo Ropro, Danke für Dein Lob. Im weiteren Verlauf habe ich nun bemerkt, daß die Dateigröße unter 3 MB bleibt, selbst wenn parallel auch die relativen Trefferabstände abgebildet werden. Diese sind ja zum Suchen von Zahlenwiederholern viel einfacher zu handhaben (Zählenwenn(...;Trefferabstand=1). Pro Tabellenblatt sind jetzt also beide Angaben aufgeführt. Gruß elementaar Und sehe gerade, daß bloß 2 MB erlaubt sind. Mist. Falsch gemerkt. Also Tabelle in zwei Teilen. Teil 1 (Beginn mit Cp 1 bis 5): EZ_FavRad_Wann_erscheint_1.02er_bis_1.10er_TrAbstände_Daten_01-05.xls

Hallo FavRad, hier ist die Auszählung. Im Gegensatz zum obigen Ausriss habe ich beim Erscheinen der Fx die absoluten Coupnummern abgebildet. Damit bei Cp 185 nicht noch die Unterscheidung Treffer/NichtTreffer gemacht werden mußte, wurde immer gezählt, bis der 1. 10er tatsächlich getroffen wurde. Per Sortieren kannst Du die Partien, die länger als 185 Cps dauerten, ja leicht identifizieren. Der Rest sollte selbsterklärend sein - sonst einfach nachfragen. Blatt Nummer 1 bezeichnet das Zählen einer Partie beginnend mit Cp 1 und Weitertransport um 185 Cps zur nächsten Partie, Blatt Nummer 2 bezeichnet das Zählen einer Partie beginnend mit Cp 2 und Weitertransport um 185 Cps zur nächsten Partie usf. Viel Spaß mit den Daten und dem Ausknobeln. Gruß elementaar Die Tabelle findet sich in meinem nächsten Beitrag; Grund: siehe dort

Hallo FavRad, das hatte ich gehofft (und erwartet), freut mich aber trotzdem! (und natürlich habe ich mit meinem Text, auch nicht im Nebensinn, angedeutet, Dein Auswertungswunsch sei der reine Unsinn; sonst hätte ich ja gar keine Hilfe angeboten). Vielen Dank für die Permanenzzahlen; ich hoffe, es war nicht zu aufwendig, sie in diese Form zu bringen. Ich schaue mal, wann ich dazu komme, ob heute noch, kann ich nicht mit p=1 versprechen, wird aber nicht all zu lange dauern. Wenn fertig, stelle ich die Auszählung hier ein. Bis dann und Gruß elementaar

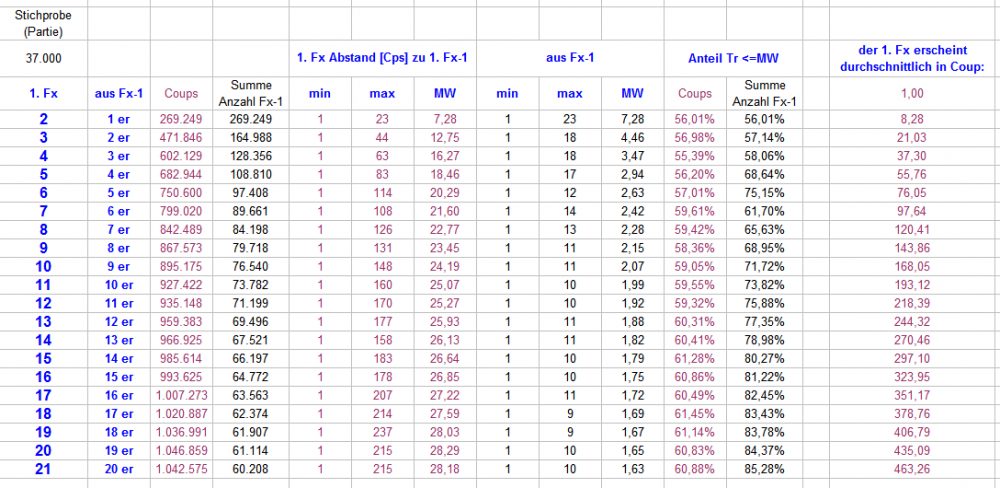
Hallo @FavRad, @Ropro, freut mich, was ihr vortragt. Merci. Das Folgende mag zwar zunächst ziemlich wenig mit dem von Euch Gesagten zu schaffen haben, gehört aber unbedingt dazu: Dazu möchte ich, bzgl. der 37.000er-Tabelle, auf etwas hinweisen, was dem verständigen Leser zwar bewußt sein sollte, was im Eifer aber öfter in Vergessenheit gerät: Die Durchschnittswerte der Tabelle werden von oben nach unten immer zufälliger. Der Befund 8,28 Cps für den 1. 2er hat ein höheres Gewicht (ist näher dran an der Wahrheit) als 463,29 Cps für den 1. 21er. Wie kann das bei doch jeweils gleich vielen 37.000 Ereignissen sein? Es wird ganz klar, wenn man sich den jeweiligen Möglichkeitsraum vergegenwärtigt: Ein 1. 2er kann frühestens im 2.Cp erscheinen, spätestens in Cp 38 muß er erschienen sein. 1.000 x 37 Ereignisse verteilen sich also auf 37 mögliche Positionen - da sollten wir, in den meisten Fällen, schon eine gute Annäherung an die Sollkurve erwarten können dürfen; was heißt: die Wahrscheinlichkeit mit dieser Teststrecke einen korrekten Durchschnittswert für den 1. 2er zu erhalten, ist hoch. (Wer es noch genauer wissen will, fertigt 10 x 37.000er-Stichproben an, und vergleicht dann die Durchschnittswerte untereinander und jeweils mit dem Gesamtdurchschnitt). (Der Extremwert von 23, (d.h. es hat in dieser Stichprobe maximal 23 Cps gedauert, bis der 1. 2er erschien), deutet aber schon an, daß diese Stichprobe für diese Frage nicht ausreichend ist!) Schon ganz anders stellt sich die Lage beim 1. 10er dar, der Möglichkeitsraum wächst gewaltig. Ein 1. 10er kann frühestens im 10.Cp erscheinen, spätestens in Cp (9 x 37) +1 = 334 muß er erschienen sein. Dieselbe Anzahl Ereignisse (37.000) verteilt sich nun auf 334 mögliche Positionen (unterschiedlicher Wahrscheinlichkeit). Beim 1. 20er ist es, analog, noch heftiger: Ein 1. 20er kann frühestens im 20.Cp erscheinen, spätestens in Cp (19 x 37) +1 = 704 muß er erschienen sein. Dieselbe Anzahl Ereignisse (37.000) verteilt sich nun auf 704 mögliche Positionen (unterschiedlicher Wahrscheinlichkeit). D.h.: mit 37.000 Ereignissen KÖNNEN die gefundenen Durchschnittswerte für den 1. 21er gar nicht so vertrauenswürdig (weil deutlich zufälliger) sein, wie die zum 1. 2er. oder umgekehrt: je höher der untersuchte Fx, desto gigantischer müssen die Datensatzmengen anwachsen, um Ergebnisse ähnlicher Validität wie bspw. Fx-10 zu erhalten. Nun rufen wir uns noch die Kurvenformen ins Gedächtnis, und das, was sich in dem vielfach von Ropro eingestellten Diagramm der idealtypischen Kurven verschiedener Fx erahnen läßt. Die beim 1.2er sehr ausgeprägte Asymmetrie der Kurve, mildert sich stetig bei höheren Fx. Das MUSS auch so sein, es ist eine FOLGE des vergrößerten Möglichkeitsraums bei Fx+1. Die so charakteristisch geformte binomische Kurve des 1. 2ers, nähert sich mit höheren Fx der Standardnormalverteilung an, und zwar umso besser, je höher der Fx. Um diesen, vollkommen folgerichtigen, natürlichen Effekt per Auszählung sichtbar zu machen, müssen Datensätze in gigantischer Menge (s.o.) bewegt werden. Dieser Effekt hat aber auch noch folgende Auswirkung: Der Abstand des Hochpunktes zu seinen beiden Nachbarn wird immer kleiner, je höher der betrachtete Fx. Als letzter Punkt (ja, ich weiß, man muß sehr viele Bälle in der Luft halten, um auch nur ansatzweise zu begreifen, was da vor sich geht, und ich bin erst bei Punkt 3!): Setzt man, geschätzt, die Validität der Durchschnittswerte ins Verhältnis zur dafür beobachteten Strecke, wird es, falls möglich, noch "erschröcklicher". Um lediglich 37.000 mal einen 1. 10er zu beobachten, mußte der F10-Spieler in dieser Stichprobe 895.175 Cps beobachten. Selbst wenn er diese Strecke mit Tricks auf eine erträgliche Echtzeit reduziert, hat er es immer noch mit einem deutlich schwankenden Durchschnittswert zu tun. Seine bis dahin erlebten Extreme sind schon mal sowieso ohne Aussagekraft (außer, daß er sie erlebt hat!) Vielleicht, wenn man das Vorgetragene etwas auf sich wirken läßt, wird so etwas deutlicher, warum ich Massentests in dieser Form so kritisch gegenüber stehe: 1. Sie fordern vom Betrachter eine sehr hohe Lesekompetenz (was sagen die Daten, und was nicht?) 2. Sie spiegeln eine Genauigkeit vor, die real nicht existiert (was bedeuten die Daten, und was nicht?) 3. Sie sind überhaupt nur geeignet, abstrakte Wissensfragen zu beantworten. Für ein praktisches Spiel haben sie minimale Relevanz. Ein riesiger Aufwand, um vergleichsweise läppische Ergebnisse zu erhalten, mit denen man praktisch (fast) nichts anfangen kann. Für mich liegt darin der größte Witz und die gleichzeitig größte Stärke in der von Ropro zur Themeneröffnung eingestellten Tabelle mit 56 Datensätzen: Das passiert real, in jederzeit erlebbarer Form, - und damit muß man zurechtkommen. In wie weit einem die Ergebnisse von Massenauswertungen bei der Bewältigung dieser Aufgabe helfen, mag jeder für sich entscheiden. Gruß elementaar

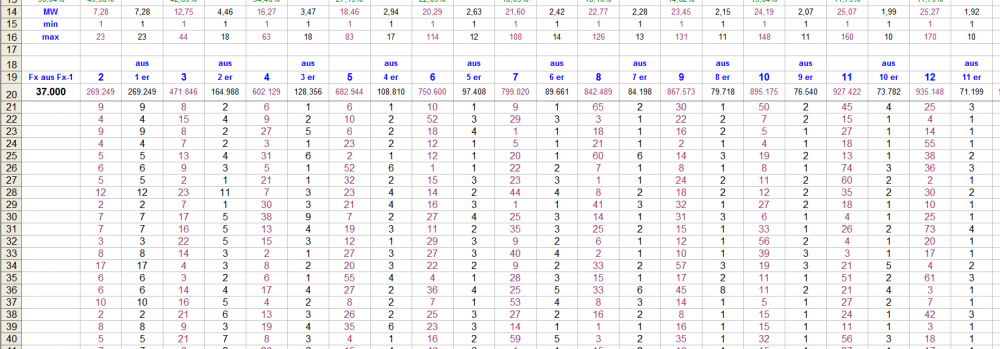
Hallo FavRad, Du willst mich doch bloß veralbern, aber um so etwas wie eine Antwort zu geben: wie es halt so geht, auch ohne zwischenzeitlich in Afrika gewesen zu sein (war hoffentlich gut?), manchmal ist der Roulette-Rechner auch noch mit anderen Teilaufgaben beschäftigt, dann wieder scheint mir ein anderer Teilaspekt interessanter (und schneller zu klären; stimmt leider mehrheitlich nicht), kürzlich tauchte hier die Frage nach Schwankungsbreiten auf, wo ich dann im eigenen Archiv Lücken entdeckte, die ich schließen wollte, usf. Richtig, in Spalte sechs können gern auch mehr Cps stehen. Wenn Du das hier einstellst komme ich schon zurecht. Damit können wir eine Stichprobe mit 1.000 Partien mit jeweils 185 Cps nacheinander auszählen. Danach können wir eine weitere Stichprobe mit 1.000 Partien und 185 Cps beginnend mit Coup 2 auszählen. Danach weitere 1.000 beginnend mit Coup 3 usf (rollierende Auszählung). Und deshalb der notwendige Überhang in Spalte 6. Wenn wir das 10 mal machen haben wir 10 Stichproben mit 1.000 Partien mit jeweils 185 Cps. Damit wird simuliert, was passiert, wenn Spieler 2 genau einen Coup später als Spieler 1 seine Aufzeichnungen beginnt. Würden wir das 37 mal machen, hätten wir Stichproben über eine Rotation mit jeweils 1 Coup Versatz. Wenn Du das aber gar nicht benötigst, können wir das auch gerne sein lassen, und uns auf die eine Stichprobe beschränken (wie Du siehst: ich reiße mich nicht gerade um die Arbeit). Damit wir möglichst über dasselbe sprechen, hier noch ein Ausriss, wie die fertige Auswertung dann aussieht: Treffer Fx in Cp aus Fx-1: In Zeile 14, 15, 16 siehst Du das arithmetische Mittel (MW) sowie Minimum- und Maximum-Wert der jeweiligen Spalte; "37.000" in Zelle "A20" ist die Stichprobengröße, daneben die summierten Werte der Spalten. Ab Zeile 21 die einzelnen Werte der Partien, von links nach rechts zu lesen: Es dauerte (in Partie 1 und einschließlich) 9 Cps bis sich der 1. 2er aus 9 Einern gebildet hatte; weitere 8 Cps bis sich der 1. 3er aus 2 2ern gebildet hatte; weitere 6 Cps bis sich der 1. 4er aus 1 3er gebildet hatte usf. Will man die absoluten Coupswerte wissen, addiert man einfach die Werte der Coupsspalten in einer neuen Spalte. Nicht aufgezeichnet wird, wann denn der 2., 3. etc. Fx-1, sofern vorhanden, erschienen ist. Etwas ähnliches kann ich auch noch betreffend Fx mit Umsatz/Treffer liefern. Falls Du weitergehende Wünsche hast, damit kann ich, so aus der Hand, leider nicht dienen. Gruß elementaar PS: Hier noch die Zusammenfassung aus obigem 37.000er Ausriss

Hallo hemjo, ach ja, "Wortklauberei", Gewinn mit F. Ich seh's ein. Alles Bestens. Gruß elementaar

Hallo hemjo, gewiß, ich habe sie auch nicht überlesen. Die folgenden einundvierzig Worte habe ich aber auch gelesen. Nun, das ist Dein gutes Recht, und niemand will es Dir verwehren. Bedauerlicherweise (und worauf bezieht sich "ebenfalls"?) wird außer der Information, daß Du mit etwas nicht einverstanden bist, aber gar nichts weiter mitgeteilt. Außer "aha" vermag kein Leser damit weiter etwas anzufangen. Eine wie immer geartete Begründung Deines Widerspruchs ist nicht vorhanden. (Und sie läßt sich, in diesem Fall, auch von niemandem erbringen, weil die Tatsachen (das sind meinungs- und sympathie-UNABHÄNGIGE Fakten) einfach andere sind). Worüber soll also gesprochen werden? Scheinbar verschärft wird Dein Widerspruch noch mit dem Aufstellen der steilen (und nicht haltbaren) These: Auch diese begründungslos (und wieder: objektiv von niemandem begründbar; es ist einfach nicht so; eine solche Stichprobe würde nur zufällig Pseudoantworten auf Deine Fragen geben). Nochmals, worüber soll denn hier gesprochen werden? Du glaubst etwas, und hast es uns mitgeteilt. Schön. Das kann man nur zur Kenntnis nehmen - fertig. Und hier möchtest Du mich verführen, Ropros Äußerung öffentlich zu interpretieren. Das werde ich nicht machen. Aber als Vorschlag, damit Du weiterkommst: Wie oft, glaubst Du, hat Ropro allein in diesem Forum, das Diagramm der idealtypischen Binomialverteilung der Fx hier eingestellt? Und hat einen Abgrund an Unverständnis und persönlicher Schmähung geerntet? Bei einer Sachlage, wo es einen interpretatorischen Spielraum gar nicht gibt, vorausgesetzt man versteht überhaupt, was da abgebildet ist. Wohlgemerkt: Nichtverstehen ist keine Schande, dann fragt man eben nach (und man macht dies möglichst höflich, sofern man so etwas wie Kinderstube genossen hat, und in dem Bewußtsein, daß der Befragte dem Frager mit der Antwort einen Gefallen erweist, und nicht fordernd, als hätte man ein Anrecht darauf), oder man macht sich mit eigener Arbeit sonstwo kundig. Man konfrontiert Fakten aber nicht mit Glaubenssätzen. Das ist der reine Unsinn. Er hat auch schon Tabellen mit den Werten eingestellt, wo jeder, den es gelüstet, nachrechnen kann, ob das alles stimmt (so er denn richtig rechnen kann). Wieviele Datensätze, glaubst Du, an real gespielten Coups wird man brauchen, damit die Kurven der gespielten Coups sich den idealtypischen genügend genau angenähert haben? Wäre es möglich, daß der betreffende Satz lediglich ein grimmiger Insider-Spaß ist, der Dich gar nicht zu berühren braucht? Gruß elementaar

Hallo FavRad, schön von Dir zu lesen. an einer Spekulation wie hemjo was gemeint hat, möchte ich mich gar nicht beteiligen (und sie auch nicht anstoßen), deshalb schrieb ich auch von "Übelwollenden" Ab und zu mal ein Wort des Dankes oder ein Satz oder eine Nachfrage, die zeigen, daß die geleistete Arbeit wenigstens verständig aufgenommen wurde, sollte aber doch eigentlich selbstverständlich sein. Ja stimmt. Mit dieser Untersuchung bin ich aber noch längst nicht fertig. Wir hatten uns auch einmal rudimentär darüber unterhalten. Die Pleinhäufigkeitsverteilung nach Art von Ropros obiger Tabelle, habe ich mit größerer Datenbasis mindestens bis zum 1. 41er (genaueres müßte ich suchen) vor Jahren erstellt. Als ich anbot, sie einzustellen, und keine Rückmeldung kam, sparte ich mir die Arbeit, die Daten für das Forum präsentabel zu machen. Alle meine Tabellen basieren ja auf vertrauenswürdigen RND-Zahlen mit Verfahren "Wenke"; Du möchtest jedoch etwas Ähnliches mit handgeworfenen Landcasinozahlen erstellen. Wie Du schon einmal schriebst, ist es schon ziemlich aufwendig, die dafür notwendigen Zahlen in der richtigen Form zusammen zu bekommen. Mit Einhalten der Chronologie UND Beschränkung auf 185 Cps kämen wir auf: mit 1.000er Stichprobengröße 185.000 Cps. Für die zweite 1.000er Stichprobe könnte wieder von vorne, aber mit Cp 2, begonnen werden usf. Also das Mindeste gesagt: 5 Spalten je 37.000 Cps ohne Handwechsel, plus in der sechsten Spalte mindestens 10 Cps (Format: .xls, zur Not geht aber auch .txt). Sehr genau wird das aber (lediglich 10 x rollierend!) dann nicht. Das durchlaufen zu lassen, ist nicht zu aufwändig, falls Du die Zahlen in der geforderten Form lieferst, kann ich Dir das anbieten. Allerdings: rechnende Excel-Tabellen kann ich Dir nicht zur Verfügung stellen. Durch den modularen Aufbau der Testumgebung, kostet ein Herausoperieren einzelner Teile einfach zuviel Zeit und ist dazu hochgradig fehleranfällig. Gruß elementaar

Naja, es lassen sich aber auch sehr lustige van-der-Waerden Reihen bilden. Besonders gefiel mir der chronologisch nacheinander gespielte Dreiklang: Mit Bild und Bibelstunde geht es dann so weiter: Wirkt zwar ein wenig düster - aber nicht ganz unfolgerichtig. Gruß elementaar

Hallo hemjo, Deine Beobachtung ist ja durchaus richtig - statt aber nun so zu formulieren, daß ein Übelwollender den Eindruck gewinnen kann (und wird), Ropros Tabelle sei falsch oder unvollständig oder gefälscht, wäre es doch sehr schön gewesen, wenn Du nur einen winzigen gedanklichen Schritt weiter gegangen wärest, und öffentlich festgestellt hättest, daß 56 (sechsundfünfzig!) Datensätze für ein Pleinspiel die von Dir erlebten Schwankungen nur zufällig abbilden werden. Hundert oder Tausend Datensätze werden es übrigens auch nicht tun. Das hätte gleich drei sehr willkommene Effekte gehabt: 1. Du würdest damit Dir und uns demonstriert haben, daß wenigstens Du verstanden hast, worauf es hier ankommt. 2. Du hättest die Möglichkeit verringert, daß gleich wieder ein Streit über Unsinn ausbricht und damit einen Beitrag dazu geleistet, daß im Forum etwas fachbezogener diskutiert wird. 3. Du hättest Ropro gezeigt, daß die Arbeit, die er sich mit der Tabelle gemacht hat (die anzufertigen, übrigens, in den paar 270 Seiten des Vorspiels schon mehrmals nachgefragt wurde, was zu leisten sich aber noch keiner der danach Fragenden in der Lage sah), daß diese Arbeit also nicht ganz umsonst war. Leider hast Du dies, in meinen Augen doch sehr Naheliegende, nicht getan. Hat das einen Grund - oder ist es einfach so passiert? Gruß elementaar

Hallo Dword, meine respektvolle Bewunderung hast Du schon längst, wie Du hier, bei eher verhaltenem Echo, unverdrossen und souverän Deine Berichte über Deine Rouletteunternehmungen einstellst und uns teilhaben läßt. Deshalb einmal ausgesprochen: Respekt und Dank! Der Zeitpunkt ist vielleicht auch nicht besonders geeignet, schließlich hast Du mit der Hardwarekalamität schon genug um die Ohren (und ausgerechnet Graphikkarte..., die Abstürze könnten aber auch mit dem notdürftigen Schließen der Prozessorspionagelücke per Software in den letzten Wochen zusammenhängen), dennoch möchte ich anregen, daß Du Dir vielleicht ein paar Gedanken über die Begriffe "starr" und "flexibel" im Zusammenhang mit dem Roulettespiel machst. Es dauert auch nicht lange, und tut nicht weh. Betrachtet man ein beliebiges Roulettezufallsgeschehen in Figuren, wird sofort klar, um was es geht: In jedem gültigen Roulettecoup MUSS eine aus 37 möglichen Zahlen fallen (sonst ist es kein gültiger Coup). In Coup 1 gibt es also 37^1 Möglichkeiten, was überhaupt nur passieren kann - mehr geht nicht. Für jeden weiteren Coup gilt, für sich genommen, selbstverständlich dasselbe. Inklusive Coup 2 gibt es also 37^2 Möglichkeiten, was überhaupt nur passieren kann. Inklusive Coup 3 gibt es analog 37^3 Möglichkeiten, und damit sind sämtliche Möglichkeiten abgedeckt - mehr ist schlechterdings nicht möglich. Nach einer Pleinrotation haben wir folglich eine konkrete aus 37^37 überhaupt nur möglichen Pleinfiguren vorliegen. Der Möglichkeitsraum vergrößert sich mit jedem weiteren Coup. Natürlich ist 37^37 eine sehr große Zahl (ich schreibe sie gar nicht erst aus), das entscheidende ist aber: die Zahl ist abzählbar und begrenzt. Mußt Du bis zum Erscheinen des letzten Restanten bspw. 150 Coups warten, hast Du eine konkrete aus 37^150 Möglichkeiten vorliegen. Die Möglichkeitszahl ist natürlich noch viel größer, bleibt aber abzählbar und begrenzt - und das für jede beliebig lange Beobachtungsstrecke. Falls sich nun an der Gleichwahrscheinlichkeit der Pleinfiguren (beliebiger Länge) durch das Vergrößern der Beobachtungsstrecke nichts ändert, sind diese standardbinomialverteilt (mit allen Folgen!). Spieler 1 verkündet nun: ich spiele immer die "1" - Urteil: starres Spiel. Spieler 2 sagt: nachdem zuerst "1" und danach "17" gefallen sind, spiele ich "1" - Frage: weniger starr? Spieler 8 sagt: nachdem zuerst "1" und danach "17"; "24"; "0"; "14"; "18"; "16" gefallen sind, spiele ich "1" - Frage: weniger starr? Spieler 36 sagt: nachdem 36 x egal was gefallen ist, aber wenigstens einmal "1", spiele ich "1" - Frage: weniger starr? Spieler 0 sagt: nach dem Erscheinen des 1. 4ers vor Coup 37, spiele ich diesen ab Coup 41 - Frage: weniger starr? Etwas durch das pure Vergrößern des Möglichkeitsraums (abzählbar und begrenzt, egal wie groß er auch sein mag) "flexibel" zu nennen, scheint nun aber doch eher der Selbstvernebelung förderlich. Flexibel wird das ganze erst, wenn nach dem Erscheinen derselben Figur (beliebiger Länge) mal so und mal wieder anders gesetzt wird. Damit allein wird aber noch nicht gewonnen. (Wie könnte der Ausgang des nächsten Coups davon beeinflußt werden, was sich die verschiedensten Spieler mehr oder minder kompliziert in "starrer" oder "flexibler" Weise ausgedacht haben?) Notwendige Voraussetzung: Gewonnen wird mit "flexiblem" Setzen erst, wenn mehr der jeweils unterschiedlichen Entscheidungen nach derselben Figur richtig als falsch sind. Mich hat das Denken in Figurenmodellen vor vielen Fallen bewahrt, ich kann es nur empfehlen. Viel Erfolg bei der Reparatur der Rechnerkiste und bei Deinen weiteren Versuchen! Gruß elementaar

Hallo 4-4Zack, freut mich, wenn er Dir gefällt (mir auch)! Und es ist zwar sehr nett, wenn Du den Urheber nennst, ist in meinen Augen aber nicht nötig; der Satz hat eine so endgültige innere Wahrheit, daß dagegen jede Urheberschaft verblaßt. Noch während ich lache, freue ich mich, daß er, dank Dir, wieder aufgetaucht ist. Gruß elementaar

Hallo Ropro, Oja, das ist, selbstverständlich und als Möglichkeit, ganz unbestritten. Es müßte allerdings nachgewiesen werden können; und damit meine ich noch nicht einmal den sauberen, absoluten Nachweis; der Nachweis: es kann keinen Spieler geben, der es innerhalb seiner Lebenszeit schafft, den großen Platzer zu produzieren, würde ausreichen. (Was aber wiederum dem absoluten Nachweis ziemlich nahe käme). Du hast ja, wenn ich mich recht erinnere, schon früher mal den Vorschlag gemacht, sich statt der Treffer doch mal (beim Pleinspiel 1 EZ) die viel zahlreicher auftretenden NichtTreffer (36 EZ) genauer anzuschauen, ohne produktives Echo allerdings. Gruß elementaar PS: Dieses riesengroße Scheunentor wird ER aber wahrscheinlich weder erkennen noch durchschreiten.

Hallo sachse, wie im Darauffolgenden zu sehen, hattest Du mal wieder recht. Hallo wolfi99, Offensichtlich hast Du auch recht - solche Reaktionen, wenn ich noch nicht einmal mit IHM spreche. Hallo Hans Dampf, Gründlicher als ER das (Selbst-)zerlegen in nun über 3.900 nur noch pathologisch nennbaren Buchstabenausflüssen (allein in diesem Forum!) besorgt, wird wohl kaum einer vorgehen können; dafür ist die eigene Lebenszeit nun wirklich zu kostbar. Nachdem ratzfatz erst vor ein paar Tagen sich die Mühe gemacht hat und hier: https://www.roulette-forum.de/topic/18025-testreihe-sven´s-spiel/?page=262&tab=comments#comment-380525 die gröbsten Rechen- und Logikfehler der Ruhlättcornifähre in bloß einem (!) SEINER Aushübe korrigiert hat, mit der sehr richtigen und ehrenwerten Begründung, in einem öffentlichen Rouletteforum dürfe der irrste Unfug nicht unwidersprochen bleiben, diese Aufgabe, meiner Meinung nach, aber niemandem allein zuzumuten ist, glaubte ich, der Kelch sei mal bei mir gelandet. Des MEISTERS Reaktion auf ratzfatzens Verbesserungen (in diesen, vergleichsweise, Subkindergartenfragen) war so vorhersehbar wie entlarvend. Ratzfatz wendet in seinen Rechenfehlerkorrekturen ja bloß die vom MEISTER HÖCHSTPERSÖNLICH zum Gesetz erhobene Faustregel der Zwei-Drittel-Verteilung an, muß sich aber dennoch von IHM maßregeln lassen ( wie immer: keine Ahnung, nicht verstanden, nicht gelesen, nicht gelesen und nicht verstanden und keine Ahnung - stimmt zwar vielleicht nicht, was ich schrieb - aber doch!) Halten wir fest: Der MEISTER verrechnet sich; eine wie immer geartete Logik in SEINEN Absonderungen interessiert IHN nicht; nur ER ALLEIN bestimmt, wann und wo die 2/3-Faustregel GESETZ ist, und wo nicht. Falls, ich betone FALLS (ist ja kaum denkbar, versteht sich), beim MEISTER etwas nicht in Ordnung sein SOLLTE, wäre es wohl hier zu finden: ER will einfach zu viele Dinge bestimmen, die nun einmal nicht SEINER Willkür unterliegen. Des MEISTERS Saga beginnt ja gemeinhin so: Starr geht nichts - also muß es flexibel gehen. Hier schon falsch - lächerlicher Fehlschluss (und zwar auf eine Art lächerlich, daß, wenn mehrfach vorkommend, sämtliche weiteren Ausführungen unter schärfstem Unfugverdacht stehen). ER produziert sowas jedoch tagtäglich und sonder Zahl. Richtig hingegen wäre: Starr geht nichts; wenn also überhaupt was geht, muß es flexibel gehen (was einschließt, daß es flexibel, möglicherweise, auch nicht geht). Wie ich schon, mindestens, dreimal in diesem Forum gezeigt habe, kann "flexibel" dann aber nur - und ausschließlich nur - bedeuten, daß exakt dieselbe (Permanenz-)Vorgeschichte zu unterschiedlichen Satzbefehlen führt. Mindestens diesen Nachweis, müßte ER aber bringen, bevor man IHM weiter zuhört, und erst recht, bevor er andere für sich arbeiten läßt. Denn DASS liebt ER ja besonders: trotz sowieso schon selbst zugesprochener Ruhlättgottgleichheit, verschmäht ER es nicht, sich mit fremden Federn zu schmücken (der arme Haller ist ungewollt Stichwortgeber SEINER falschen Ansichten, roli888 hat SEIN wirres Gestammel überhaupt erst in eine in sich folgerichtige Form gebracht und spielt sogar vor, Albert hat IHM seine Hundertstel Prozent "Überlegenheit" verschafft (Hundertstel Prozent besser als -2,7%, wohlgemerkt) usf.). Ist die ganze Spielanlage (Beginn mit einer (!) EZ) aber schon so, daß eine Überprüfung kaum einmal möglich sein wird (wegen begrenzter Lebenszeit oder unsinnig langer Simulationsstrecken), sind wir hier schon (mit lediglich zwei (!) Voraussetzungen: 1. Beginn mit Fehlschluss; 2. Spiel auf EZ) auf dem Gebiet des Glaubens. Und diesen Glauben fordert ER ja auch, mehr oder minder tobend, ein. Und so baut sich SEINE ganze Spielweise auf einer falschen Aussage nach der anderen auf. Auf die Verwirrtheit SEINES BIN- und POI-Geraunes habe ich übrigens schon in meinem allerersten Beitrag zu diesem Forum hingewiesen. Also nein, ich zerlege IHN nicht, Glaubensleute muß man sich, in dieser Hinsicht, vom Leib halten. Es sollte genügen, ab und zu, auf nachprüfbare Fakten zu verweisen. Gruß elementaar

Hallo Take_7, zu des MEISTERS Spiel habe ich mich noch nie geäußert, und werde es auch jetzt nicht tun. Und es liegt erst recht nicht in meinem Interesse, irgendjemand die Freude an seinem Spiel zu mindern. Das hält doch sowieso jeder, wie er möchte. Nach meinem Eindruck fassen es die Spieler seines Spiels ja auch sowieso eher als die eigentliche Herausforderung auf, in seinem dynamisch und flexibel sich widersprechenden Regelgestrüpp nur ja alles "richtig" zu machen (was "richtig" ist, sagt ja der MEISTER hinterher), als eine dauerhaft gewinnende Spielweise für sich zu entdecken. Denn ginge es hauptsächlich darum, müßte doch jedem, mit einem auch noch so kleinen Stück Restverstand Gesegneten, sofort seine massenhaften Falschaussagen heftig zu denken geben. Und läßt man selbst das noch durchgehen (von wegen "dicksten Kartoffeln" und den Bauern), bleiben noch die eklatanten Logikabgründe, die sich selbst innerhalb seiner Wahnwelt nicht übersehen lassen. Und damit in diesem Leben niemals der saubere Nachweis geführt werden kann, ob sein Spiel doch etwas taugt, hat er ja gründlich vorgebaut (Wahl der Chancengröße, Flächenprogression, Stückeprogression, Spieldauer, erhoffter Gewinn, läßt sich nicht programmieren, weil zu flexibel, mit "Schießbuden-"zahlen schon mal gar nicht, etc. ; am salvatorischsten jedoch mit dem Axiom: wenn einer nicht gewinnt, MUSS es am fehlenden Verständnis liegen oder der Gier). Nur mal vorgestellt: würden sich auf einmal 1.000 Leute finden, die es wie Roli888 machen, und jeweils 100 Partien aus unterschiedlichen Zahlenquellen spielen, hätte der Spuk, wahrscheinlich, immer noch kein Ende, denn der MEISTER würde es sich bis auf sein Sterbebett nicht nehmen lassen, jedem einzelnen Spieler in jeder einzelnen Partie seine jeweiligen Fehler sowie seine allgemeine Ahnungslosigkeit und Dummheit nachzuweisen. Und als letztes: dem ganzen verrauschten Zinnober liegt dieselbe, durch ständige und immerwährende Wiederholung auch nicht wahrer werdende Falschaussage zu Grunde, man könne mit der Verknüpfung mehrerer Spiele (Sichtweisen, Kugelfenster, TP-Abgleich etc.), die jede für sich genommen -2,7% vom Umsatz produzieren, eine dauergewinnfähige Treffererkenntnis generieren. Den Gläubigen erscheint das einleuchtend, die Anderen wissen, daß es nicht so ist. Wozu also der ganze Lärm? Gruß elementaar

Hallo Take_7, die Frage darfst Du aber doch nicht "jemand" stellen, sondern nur dem EINEN - wo kämen wir denn dahin? Wir anderen kennen sie zwar, die sind dann aber garantiert gaaanz falsch und führen nur in den Verlust. Die richtigsten Werte sind nämlich totaaal abhängig davon, wer gerade spricht, und wer was gerade nicht verstanden hat. Weil ja außerdem beim MEISTER Zéro zu TP 1 gehört (und sich (in seiner Welt) dadurch beim BIN und POI ja gar nichts ändert), ist das auch komplett und super und logisch. Das ist ja auch nur ein Geheimnis seines Erfolgs: die situationsgerecht richtigen Werte kennt nur er. Merke: der POI ist richtigster als wie den BIN, wenn trifft. Gruß elementaar

Jetzt macht ihr mir aber wirklich Angst. Verstörende Vorstellung!

Also mein Favorit ist eindeutig das Kugelfensterschneiden - das ist klasse und macht Spaß! Das hält alles geschmeidig, also schon starr, aber nicht zu starr- geschmeidig-starr eben. Dicht gefolgt vom Pleinsektorlückensatz, der paßt so wunderbar in die Systematik, und hat außerdem so einen tollen Namen. Der bringt's - unbedingt. TP-Abgleich ist dagegen Kinderspiel. Aber am wichtigsten: immer nur schneiden oder Lücken setzen am BIN-punkt (gibt Erfüllung), oder ganz ganz kurz davor oder auch danach, weil da die Treffer am vielsten, und sonst beim POI nachgucken. So - fertig jetzt, muß mein Erdloch fegen, und bald ist Luna wieder voll.

Hallo Scoville, hier scheint es aber doch angebracht, darauf hinzuweisen, das die mathematische Rechengröße "unendlich" ein reines Geistesprodukt ist. Bei all seinen Verdiensten in der neuzeitlichen Mathematik, darf man dennoch nicht vergessen, daß es "unendlich" in diesem Universum NICHT gibt. Zu jeder Zahl, und sei sie noch so groß, oder klein, oder schräg, oder unvorstellbar, gibt es in diesem Universum das entsprechende Produkt "Zahl x 2". Praktisch ist es durchaus möglich, daß ein Superpechvogel auf eine NichtTreffer-Serie trifft, die von ihm per Verdopplung fordert, mehr Stücke auf den Tisch zu legen, als es (geschätzte) Atome im Universum gibt - physisch also ganz unmöglich. Dies läßt sich jedoch sehr einfach lösen, indem er unbegrenzten Kredit erhält (Menge N). Jeder (richtige) Beweis, der für sein Zustandekommen mit der Größe "unendlich" hantiert, ist unbestreitbar richtig, muß aber in diesem Universum auf seine praktische Relevanz überprüft werden. Die Freude an der Tautologie ist in der Mathematik und unter Mathematikern ja ganz besonders ausgeprägt. Übrigens hantieren wir auch im täglichen Leben erfolgreich und problemlos mit reinen Geistesprodukten. Physisch wird mir mein Obsthändler jedoch (lassen wir mal Termingeschäfte außer Acht) niemals " - acht Äpfel" verkaufen können. Gruß elementaar

Hallo FavRad, vielen Dank für Deine Stimme der Klarheit und Vernunft. Man kann es gar nicht dick genug schreiben - und zwar beide Teile. Vollkommen richtig. Es ist weder Hexenwerk, noch Raketenwissenschaft noch Quantenphysik. Jeder, der in der Lage ist zu zählen, kann das. Das ist allerdings Voraussetzung, und macht eindeutig mehr Arbeit, als jeden Tag die lächerlichsten Glaubenssätze ex cathedra zu posaunen. Wie es überhaupt irgendeinen (mindestens "klassischen") Pleinspieler (und nicht nur die!) geben kann, der sich noch nicht dieser Mühe unterzogen hat, ist einigermaßen, und bis ins Absurde, rätselhaft. Gruß elementaar

Ein "nach" reicht auch. Ganz genau und richtig! DEINER Meinung nach -- und NUR Deiner Meinung nach. Zeigt sich hier doch schon Dein fundamentales Nichtbegreifen, indem Du behauptest, zu dieser Frage könne man überhaupt eine individuell womöglich unterschiedliche Meinung haben. Das ist hier nicht der Fall - hier gibt es nur - und ausschließlich - richtig ODER falsch. Und zwar genauso klar wie die einzig richtige Lösung zur Frage 1 + 1 =? ZWEI lautet. Meinung, Glauben, evtl. vorhandene Verdienste bei der Phantasietortenbäckerei oder des Spieleerfindens spielen KEINE, und zwar GAR KEINE, Rolle. Allein schon die Annahme, man könne dazu eine Meinung haben, ist restlos disqualifizierend für jede weitere Diskussion.