elementaar

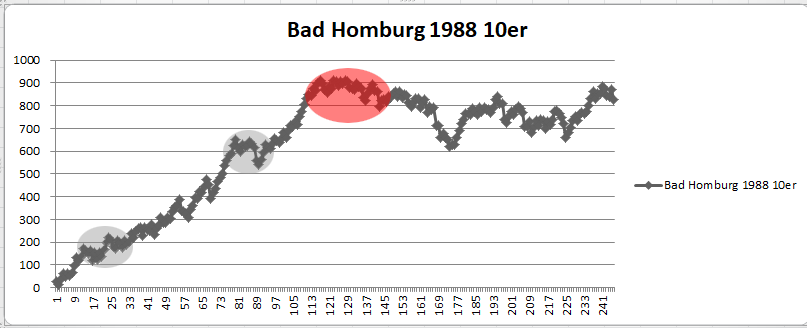
Hallo FavRad, da warst Du aber fleißig, und daß bei warmer Wintersonne, bei uns schüttet es und ist finster. Auch "geballte" Logik ist aber nicht in der Lage Tatsachen zu widerlegen, höchstens sie zu erklären. In aller Schnelle zu Deiner Saldokurve selbst: Die auffälligsten Stellen, bei reiner Kurvendiskussion habe ich markiert. Zweimal "grau" unterlegt: Beides "Zitterstellen": Seitwärtsbewegung ungewissen Ausgangs. "Rot" unterlegt: Endgültiger Ausstieg, wegen deutlichem Überschreiten der Länge der beiden vorigen Zitterstellen UND starker Entfernung vom letzten Hochpunkt. Gruß elementaar PS: Bitte entschuldige, trotz "wibbelig"keit, zu mehr reicht meine Zeit heute nicht mehr - vielleicht die Tage.

Hallo Ropro, freut mich sehr, zu lesen, daß wir mit unterschiedlichen Methoden auf eine ähnliche Sachlage gestoßen sind. Wenigstens noch einer, den das beschäftigt. Das wäre eine mögliche Lösung und perfekt formuliert (deshalb von mir fett markiert). Seit bestimmt zehn Jahren knabbere ich daran herum, und bin bloß marginal weitergekommen. Wobei das "Könnte" für mich einen mindestens doppelten Sinn hat. 1. "könnte" als: reichen meine persönlichen Fähigkeiten, und wenn nicht, was und wo könnte ich lernen. 2. "könnte" als: ist es überhaupt möglich? Bei chaotischem Geschehen noch unbekannten Charakters. Verschiedene Formen, auch einstellbarer, "Unschärfe"-filter z. B. haben bei mir versagt, und waren teilweise sogar schlechter als visuelle Beurteilung (perfiderweise aber "natürlich" nicht so viel schlechter, als daß man etwas daraus hätte machen können). Gutes Gelingen! es ist ein Haufen Arbeit. Gruß elementaar

Hallo Ropro, das war in diesem Fall nicht ganz unbeabsichtigt. Es ist aber auch kein Geheimnis: Starte bei einem beliebigen Fx, wenn es sein muß beim 1. Einer. Setze diesen einmal nach. Bei Treffer evtl. Neubeginn. Bei NichtTreffer warte auf den, im Beispiel 1. 2er. Setze diesen einmal nach. usf. In dieser Frage sind vielerlei Versuchsanordnungen denkbar; z. B.: Wann (und wie teuer) erscheint der 1. Zweier der 1. Fx er. Dies sind jedoch alles nur Nebenprodukte der eigentlichen Frage, mit der ich leider noch längst nicht fertig geworden bin: Bei diesen Massenauszählungen fiel mir irgendwann auf, daß sich die Maximumzahl der am neuen Fx als Möglichkeit beteiligten Zahlen nur noch sehr zäh verringert. So ist es bspw. ziemlich egal, ob man auf den 1. 15er oder den 1. 20er spielt, immer muß man damit rechnen, auch einmal ca. 10 Zahlen auf einmal setzen zu müssen. Da in jeder Fx-Stufe als durchschnittlicher Umsatz 37 Stück herauskommen sollte, sich die durchschnittliche Coupstrecke bis zum Treffer zwischen 15er und 20er aber um ca. 1,5 Coups erhöht, wird man das Maximum beim 20er etwas seltener sehen. Aber wie verhält es sich mit dieser Maximumbeteiligung: geht die Zahl weiter zurück? stetig bis 1,xx? oder findet die Kurve einen Tiefpunkt und steigt dann wieder an? Verbunden damit natürlich die Frage: unterscheidet sich bspw. ein 1. 1000er noch signifikant von jeder anderen Zahl? Wie gesagt, ich bin noch längst nicht fertig damit, und habe folglich keine Antwort. Sauber die -3 Sigma gerissen, wie man sichs wünscht. Ganz recht, das muß man mühsam per Auszählung feststellen, und das dauert! Leider SEHR viel länger, als man es gerne hätte. Gruß elementaar

Hallo FavRad, Danke ebenfalls, und besonders freut es mich, daß Du das Wort "Interpretation" benutzt. Denn leider sind die schönsten Auszählungstabellen kaum etwas wert, wenn sie nicht auf halbwegs verständige Leser treffen, und können, wo das nicht gegeben ist, sogar Schaden anrichten. Als Beispiel mag die Zeile zum Erscheinen des ersten Zweiers dienen, wo als maximal aufgetretener Abstand zum ersten Einer "23" eingetragen ist. In sehr viel umfangreicheren Untersuchungen habe ich persönlich dort schon die Zahl "31" verzeichnet gesehen, d.h. es dauerte in diesem Fall bis Coup 32, bis der erste Zweier erschien. Sofern man nun nicht unterstellt, die Tabelle solle vorsätzlich in die Irre führen (was gewiß nicht der Fall ist, das schließe ich, für mich, kategorisch aus), weiß man als verständiger Leser, daß die min/max-Werte eher illustrativen Charakter haben, und daß diese Auszählung ausschließlich auf die Durchschnittswerte abzielt. Und dafür sind 37.000 Ereignisse genügend. Um deutlichere Ausbleiberextrema zu sehen, muß man dieselbe Stichprobengröße geschätzt noch mindestens weitere 14 mal produzieren; um dann, nebenbei, festzustellen, daß sich die Durchschnittswerte währenddessen nur noch im 1/10tel-Bereich ändern. Alle meine Massenauswertungen sind vertauenswürdige RNG-Zahlen, die zuvor dem Verfahren "Wenke" unterzogen wurden. Kurze Begründung warum: Nach fast zwanzig Jahren ballistischen Spiels in Landcasinos, glaube ich , für meine Zwecke, halbwegs beurteilen zu können, was dort mit Croupier/Kugel/Kessel geschieht. Der Grad an Zuverläsigkeit der opto-elektronischen Anzeigen ist mir ebenfalls aufgefallen. Deshalb sind für mich Landcasinozahlen nur vertrauenswürdig, wenn ich sie selbst aufgeschrieben habe, und selbst dann nicht zu 100% (Schreibfehler). Um zu erfahren, was Zufall so anrichtet, sind diese Zahlen, meiner Ansicht nach, nicht gut geeignet. Um jeglichen ballistischen Effekt auszuschließen, und außerdem die Auswirkungen von Notierfehlern zu minimieren, werden ausschließlich Zufallszahlen von vertrauenswürdigen Zufallsgeneratoren (RND) herangezogen (u.a. Geiger-Müller-Zählrohr, Rausch-Generator), die danach noch dem Verfahren “Wenke” unterzogen werden. Das Verfahren “Wenke” (Genial, und hier im Forum zu finden!) Die RND-Zahlen stehen in Spalten zu je 37.000 Stück. Per Excel-Zufallszahl() wird für jeden Coup jeweils eine neue Spalten- sowie Zeilennummer bestimmt, aus der die RND-Zahl entnommen wird. Vorteil: Für jedes Experiment werden vollständig neue Permanenzen verwendet, damit besteht keine Gefahr des unerlaubten Abschneidens oder der Rückoptimierung. Nachteil: Läßt man die jeweils neuen Permanenzen nicht stetig mitschreiben, kann jede Untersuchung nur exakt die Fragen beantworten, die vorher gestellt wurden. Das nachträgliche Beantworten neuer Fragen ist in den meisten Fällen aufwendig bis nicht möglich. Noch eine Anmerkung zu den angegeben BIN-Werten, die hier immer wieder kursieren (meine Verwunderung darüber ist längst entschwunden): Ich vermute, sie sind irgendwelchen Haller-Tabellen entnommen. Da muß man aber leider feststellen, daß diese überwiegend nicht verläßlich sind. Das ist dabei höchstens ein milder Vorwurf an Haller, bei der Unzahl an Zusammenstellungen und dem druckfertig machen per Hand, verrutscht schon mal eine Zeile, oder fehlt eine Angabe schon mal ganz. Ärgerlicher ist da schon, daß manchmal auch die mitgeteilten Formeln entweder nicht richtig gedruckt wurden oder (selten) ganz falsch sind. Illustrativ sind sie brauchbar, hat man jedoch eine spezifische Frage und will es genau wissen, empfiehlt es sich unbedingt, die betreffende Tabelle persönlich nachzurechnen, damit man nicht Fehlschlüssen aufsitzt. Als Beispiel mag hier das durchschnittliche Erscheinen des ersten 9ers und 10ers dienen. Wie in Deiner Aufstellung zu sehen, würden im Vergleich zum angegebenen BIN-Wert diese beiden jeweils mindestens 9 Coups früher erscheinen, mit Deinen eigenen Auszählungen sogar noch viel früher; das würde (auf dieser Spielstrecke) locker für ein gewinnfähiges Spiel (ganz ohne Kugelfenster) reichen. Bevor man nun aber in "Heureka"-Jubel ausbricht, oder gar echtes Geld auf den Tisch legt, muß man sich schon persönlich davon überzeugen, ob der angegebene BIN-Wert auch richtig errechnet wurde. Zu diesem Zweck ist, statt der oben mitgeteilten Tabelle, die die durchschnittlichen Trefferabstände abbildet, wesentlich besser eine Tabelle geeignet, die die durchschnittlichen Umsatzabstände aufzeigt. Wenn gewünscht, kann ich die betreffenden Daten aufbereiten und hier veröffentlichen. Aus Zeitmangel kann das allerdings etwas dauern. Deinen Spiel-/Forschungsvorschlag finde ich, zumal im Landcasino, keineswegs abwegig. Interessanterweise bin ich dabei, eine vage ähnliche Frage zu überprüfen: Man spiele nach Erscheinen des jeweils 1. Fx diesen jeweils 1 mal nach. Dabei interessiert mich weniger eine evtl. erhöhte Trefferwahrscheinlichkeit (wäre schön, aber wer's glaubt), als vielmehr die größten Trefferabstände. Und weil das eine unmittelbar mit dem anderen verbunden ist, könnten sich vielleicht die einzelnen, winzig erhöhten Trefferwahrscheinlichkeiten zu insgesamt deutlich verringerten Trefferabständen addieren. Mal sehen, ob und was dabei herauskommt. Vom praktischen Spiel (ohne eine Menge Scheinspieler unfaßbar langweilig) wollen wir mal gar nicht reden. Gruß elementaar

Hallo FavRad, vielleicht hilft Dir folgende kleine Auszählung weiter. Ich habe noch mehr, nur leider im Moment viel zu wenig Zeit, die Daten aufzubereiten. Gruß elementaar

Hallo Fritzl, Trotz roter Hervorhebung in Zitat und Frage, bin ich, auch späßchenhalber, vollkommen überfragt. Dies liegt natürlich zu allererst an meiner restlosen Inkompetenz im Aufspüren von Millionären. Ich wüßte gar nicht, wie man das macht, zumal mir auch gar nicht bewußt war, daß es überhaupt Leute gibt, die es lohnenswert finden, zumindest einen Teil ihrer Lebenszeit dem Auffinden von Millionären zu widmen. Und im Erfolgsfall: was macht man dann mit ihnen (den Millionären)? Oder ist das so ein Ding, wie mit Flugzeugen oder Lokomotiven oder Vögeln? Hat man ein Exemplar gesichtet, schreibt man ein ausführliches Protokoll zum Ereignis, und beim wöchentlichen Clubtreffen kann man sich in der ehrerbietigen Anerkennung der anderen Vereinskollegen sonnen? Ich weiß es nicht, und kann im Gegenteil versichern, bisher habe ich meine Lebenszeit ausschließlich für andere Dinge verwandt. Auch im Spielsaal bin ich bisher immer nur auf mich deutlich fesselndere Ereignisse gestoßen. Mag sein, daß auch dies eine Frage persönlicher Indolenz ist. Was allerdings das von Dir gewählte Zitat betrifft, da bin ich mir doch ziemlich sicher, wirst Du weder einen einzelnen noch gar mehrere Millionäre, weder zu Beobachtungs- noch sonstigen -zwecken, finden können, und zwar schlicht, weil sie sich in diesem Satz gar nicht aufhalten, sozusagen zu 100% absent sind, und zwar sowohl persönlich, wie auch im semantischen Abbild. Insofern fragst Du zu recht: "Wo sind sie denn?" Andererseits: warum sollten sie überhaupt da sein? Was hätten sie in dem Satz zu suchen? Ich weiß zwar nicht, was Millionäre genau und sonst so machen, fände es allerdings ziemlich ungehörig von ihnen, wenn sie sich ungefragt in meinen Sätzen herumtrieben, und, unerkannt und unbeaufsichtigt, womöglich wer weiß was anstellten. Also, ich persönlich, vermisse sie in diesem, meinem Satz nicht. Es gibt auch, glaube ich, noch weitere Sätze, von mir oder Anderen, da wollen wir mal nicht kleinlich sein, in denen keine Millionäre vorkommen. Ob sie dort vermißt werden, ist mir noch nicht bekannt oder gar auffällig geworden. Zusammenfassend, und obwohl in dieser Frage eher das Gegenteil eines Fachmanns (s.o.), kann ich die Vermutung wagen, daß Sätze, in denen das Wort "Millionär" nicht vorkommt, zum Aufspüren desselben nicht allererste Wahl sind. In wie weit Dir dies allerdings weiter hilft, weiß ich auch nicht. Gruß elementaar

Hallo richi56, vielen herzlichen Dank für Deinen ausgezeichneten Bericht Deiner doch sehr umfangreichen Testreihe aus der Praxis. Die geschilderten Einsatzhöhen in Verbindung mit der Auszahlung lassen den nicht geringen Aufwand schon erahnen. Umso dankbarer bin ich, daß Du uns Dein Resumée zur Verfügung stellst. Ich möchte hoffen, daß Du damit nicht nur mir eine Freude gemacht hast. Das ist natürlich sehr unerfreulich, wenn ich auch hier ein Minimum an Trost herauslese. Für die aufgewendete Energie und Zeit bleibt es zwar ein schmales Minimum, für die "Ehre" hast Du allerdings Erkleckliches geleistet. Dank Dir haben wir nämlich in diesem Thema jetzt den eher selten anzutreffenden Fall, daß ausführliche abstrakte Betrachtung und nicht minder ausführliche Praxisberichte vereint sind. Daß Abstraktion und Praxis letztendlich zu sehr ähnlichen Ergebnissen kommen, ergibt einen schönen Gewinn für alle verständigen Leser. Und das ist schön, wie ich finde. Hoffentlich bist Du über die erzielten Ergebnisse nicht zu zerknirscht; daß Du Dich trotzdem noch zum Verfassen Deines Berichtes aufraffen konntest, ist da besonders bemerkenswert und ehrenhaft. Sehr gut und herzlichen Dank. Ich ziehe den Hut! Gruß elementaar

Hallo Ropro, So ins Allgemeine gewendet, ist das natürlich eine äußerst verzwickt zu beantwortende Frage. Und manches wird wahrscheinlich nur der Fortgang der Zeit klären. Für unabdingbar halte ich allerdings intellektuelle Redlichkeit aller Diskutanten als nicht hinterfragbare Grundvoraussetzung. Nur so haben wir überhaupt die Chance (=NICHT Gewißheit), irgendetwas über uns selbst und die Welt herauszufinden, was Bestand hat. Gruß elementaar

Hallo 4-4Zack, Eine der beruhigendsten Eigenschaften von Fakten, ist ihre Fähigkeit, auch ohne das Verständnis von Irgendwem als wahr und richtig zu existieren, und ihre Wirkkraft zu entfalten. Eine der bittersten ist allerdings, daß es mitunter enorme Kosten (an Geld, Zeit, Menschenleben) verursacht, bis eine relative Mehrheit sich ihrer anbequemt. Gruß elementaar

Das Ding heißt arithmetischer Mittelwert. Es gibt auch noch u.a. geometrische, quadratische etc. Mittelwerte. Alles Mathematik, "math. Mittelwert" sagt also gar nichts bzw. ist ausgemachter Unsinn. Keinen dieser Mittelwerte muß man schätzen. Im Falle irgendeines Pleintripels beträgt der arithmetische Mittelwert: 1/(1/37^(3-1))=1.369. Wer ist überhaupt dieser "aller"? Der verstümmelte Cousin vom Haller? Gemeint ist wohl "alle"; und damit ist der nächste Verständnisfehler angesprochen: Wie ist es möglich, daß ein Mensch allein soviel Unsinn absondert? Nein - "bedeutet" es "dann" nicht! Denn natürlich ist auch die Wahrscheinlichkeit p = 1/1.369 binomialverteilt und lediglich bei sehr großen Zahlenmengen wird man den arithmetischen Mittelwert erblicken. Zum praktischen Spiel nützt einem das aber (längst bekannt) gar nichts, weil gilt: Die Binomialverteilung hat den Erwartungswert np.

Die Binomialverteilung besitzt den Erwartungswert np. n = Anzahl der Versuche p = Wahrscheinlichkeit eines Versuchs

Hallo @Ropro, sehr gut dargestellt! Besser wird man es kaum machen können; und eine weitere Bereicherung in Sachen Grundlagenwissen und -methoden. Vielen Dank! Gruss elementaar

Hallo @Juan del Mar , Dürfte ich Dich bitten, einige Quellenangaben zu machen? Diplomarbeit: Zu welchem Thema und aus welchem Gewerk? Titel, Autor, Suchstring? Falls Du Dir die Mühe machst: vielen Dank im Voraus! Und zu dieser Gelegenheit, selbstverständlich: Hallo @Roli888, Es freut mich sehr, Deine hervorragende Arbeit hier und mit diesem Thema zu verfolgen. Und ganz unabhängig vom Ausgang, wie Du die Sache angehst ist mustergültig und souverän - vielen Dank dafür! Hoffentlich bleibt Dir Dein langer Atem noch lange erhalten. Gruß elementaar

Hallo @wiensschlechtester, Danke für das schnelle und kompetente Einspringen! Hallo @sachse, aber ja, das steht ja sowieso außer Frage. Gruß an Euch beide elementaar

Hallo @sachse, Deine Angaben beziehen sich darauf, was 10 Mio Spieler (bei EC mit 19/37) im nächsten Coup erleben werden. Oben wird aber ein Spiel über eine begrenzte Satzcoupstrecke beschrieben, welches bei Saldo +1 oder Ende der Spielstrecke endet. Verabreden sich 10 Mio Spieler dementsprechend (mit 18/36) zu Spielen über maximal Coupstrecke x, werden bei 3 gesetzten Coups 6,25 Mio Spieler Saldo +1 haben, der Rest Minussalden unterschiedlicher Höhe bei 5 gesetzten Coups 6,785 Mio Spieler Saldo +1 haben, der Rest Minussalden unterschiedlicher Höhe bei 7 gesetzten Coups 7,266 Mio Spieler Saldo +1 haben, der Rest Minussalden unterschiedlicher Höhe Am neg. EW ändert sich natürlich nichts; dennoch können deutlich über 50% der Spieler mit +1 Stück nach Hause gehen. Gruß elementaar

Hallo @Scoville, ja gewiß - kein Problem damit. Ich gehe auch davon aus, daß @sachse obig Dargelegtes ebenfalls weiß. Mein Beitrag entsprang einer gewissen Unwilligkeit darüber, daß derartiger Kinderkram hier scheinbar nicht als Selbstverständlichkeit vorausgesetzt werden kann. Also, falls nötig, Entschuldigung für die partielle Ungeduld. Gruß elementaar

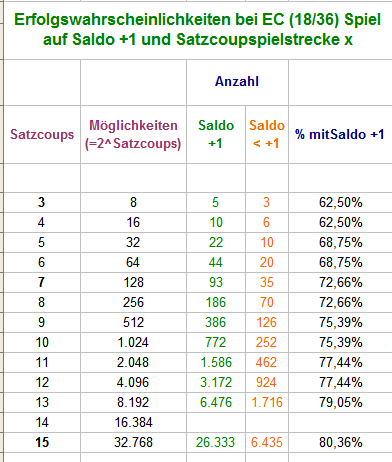
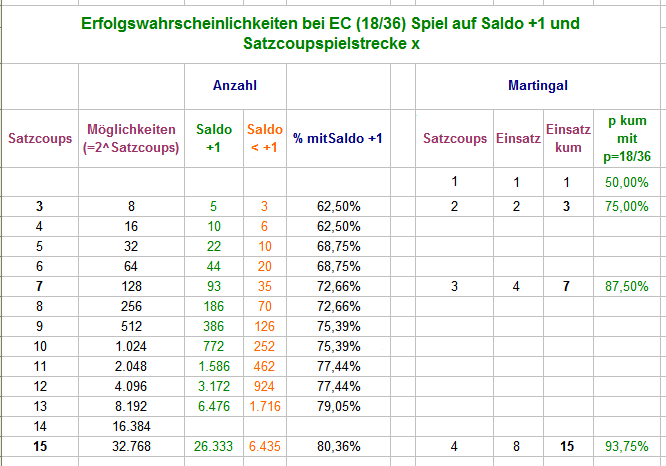
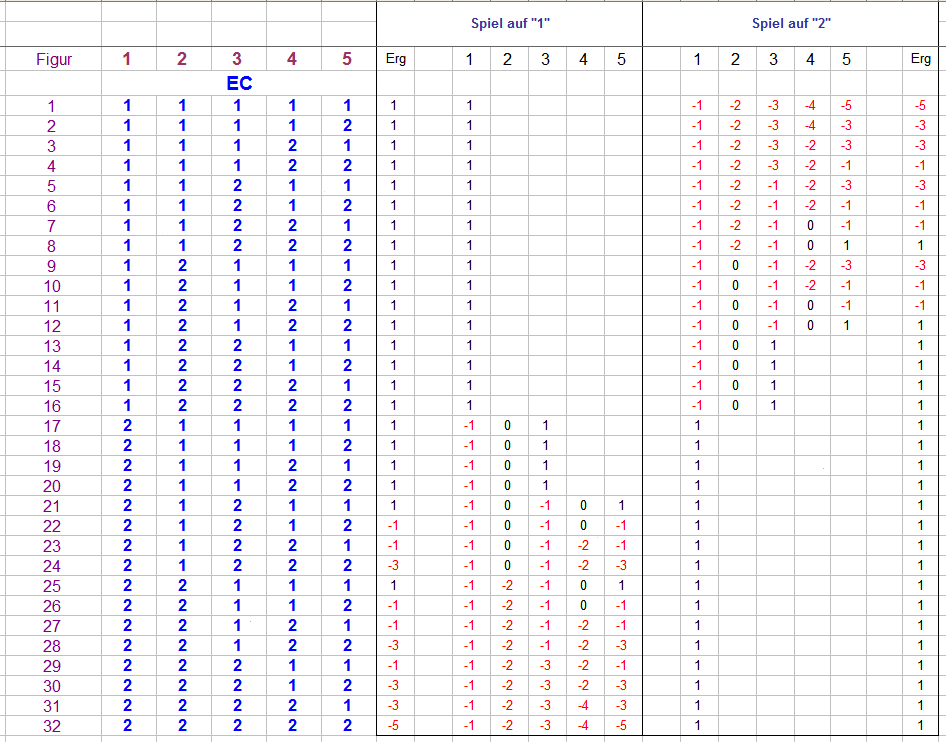
Hallo @sachse, es geht um die simple Frage der Erfolgswahrscheinlichkeit für folgendes einmal (!) zu spielende Spiel: Gleichsatz auf EC; Satzcoupstrecke x; Spiel bis Saldo +1 (dann Spielende) oder Satzcoupstrecke x Ende (dann auch Spielende). Danach NIE wieder spielen. Außer dem Aktualisieren des Saldos muß man dazu überhaupt nichts rechnen. Für überschaubare Satzcoupstrecken schreibt man sich alle möglichen Fälle auf (Figuren), führt die Salden gemäß Spielregel für alle möglichen Fälle, und ZÄHLT, wie oft man Saldo +1 erzielt. Über Zählergebnis/mögliche Fälle kommt man zur richtigen Prozentzahl der Erfolgswahrscheinlichkeit. In der folgenden Tabelle sind die Ergebnisse bis Satzcoup 15 (alles ohne Zéro) zusammengefaßt. Sofort ersichtlich ist, daß Satzcoupstrecken mit gerader Anzahl an Sätzen zwar den Umsatz, nicht jedoch die Erfolgswahrscheinlichkeit erhöhen; in der Spielpraxis wären diese also zu meiden. Mit äußerst überschaubarer Geistesleistung läßt sich aus obiger Tabelle ableiten: Bei jedem Spiel mit Erfolgswahrscheinlichkeit > 50% werden wir sowohl öfter als auch längere Plusserien sehen. Warum derartige Banalitäten (in einem Rouletteforum!) als Inhalt des Nähkästchens deklariert werden, erschließt sich mir allerdings nicht. Vielleicht, weil sie scheinbar immer wieder verkündet werden müssen? Ich weiß es nicht. Denn geht es darum, sich häufigere und längere (Partie-)Plusfolgen zu konstruieren, drängt sich der Vergleich mit dem Martingal (oder dem Vergrößern der Chancengröße bis 35/37) ja geradezu auf; beim jeweils selben Kapitalbedarf sieht das dann so aus: Beim gleichzeitigen Spiel auf bspw. Rot/Schwarz ergeben sich nach dem ersten gesetzten Coup dann folgende Aussichten (hier für die 5er-Figur): Der entscheidende Satz bei dieser Betrachtung sei aber nochmals wiederholt: Eine Partie spielen (EW siehe oben) - danach NIE wieder spielen. Gruß elementaar

Hallo Hans Dampf, Da hast Du natürlich zweifelsfrei recht. Und vielen Dank für das Aufzeigen: In einem von 37 möglichen Fällen ist das Abdecken von 37 verschiedenen Zahlen in der Tat nicht vollkommen sinnlos. Bisher bin ich immer davon ausgegangen: Will man mehr als 18 Zahlen in einem Coup abdecken, läßt sich der durchschnittliche Verlust mit geschickter Satzakrobatik von -2,7% auf bestenfalls ca. 2,03% drücken. (Ich glaube sogar mal etwas ausgeknobelt zu haben, bei dem man auf knapp unter -2% landete, habe aber vergessen, wie das ging.) Das versteht sich sozusagen von selbst: daß der Spieler situativ die für sich günstigste Möglichkeit des Setzens wählt. Der oben erwähnten Spielbeschreibung "Spiel auf den ersten Plein-Zweier" könnte man nun eine Tabelle gegenüberstellen, bei der errechnet wird, was maximal kluge Sätze bewirken würden. Dazu wären Neuberechnungen ab Coup 20 (19 Einzelzahlen) bis Coup 38 nötig. Beim gewichteten Ergebnis würde ich dann statt -1/37 ca. -0,75/37 erwarten. Mir ist nur leider nicht klar geworden, in wie weit diese Tatsachen die Gesamtargumentation verändern würden. Falls dies bei mir die Wald/Baum-Situation ist, wäre ich für einen weiteren Hinweis dankbar, und, falls die Erläuterung nicht zu viel Mühe macht: wie sähe Deine Argumentation im obig beschriebenen scheinbaren Widerspruch aus? Gruß elementaar

Und bei gemeinsamer Kutschfahrt von Armeechef und offizieller Maîtresse heißt es: "Des Königs Schwert und seine Scheide."

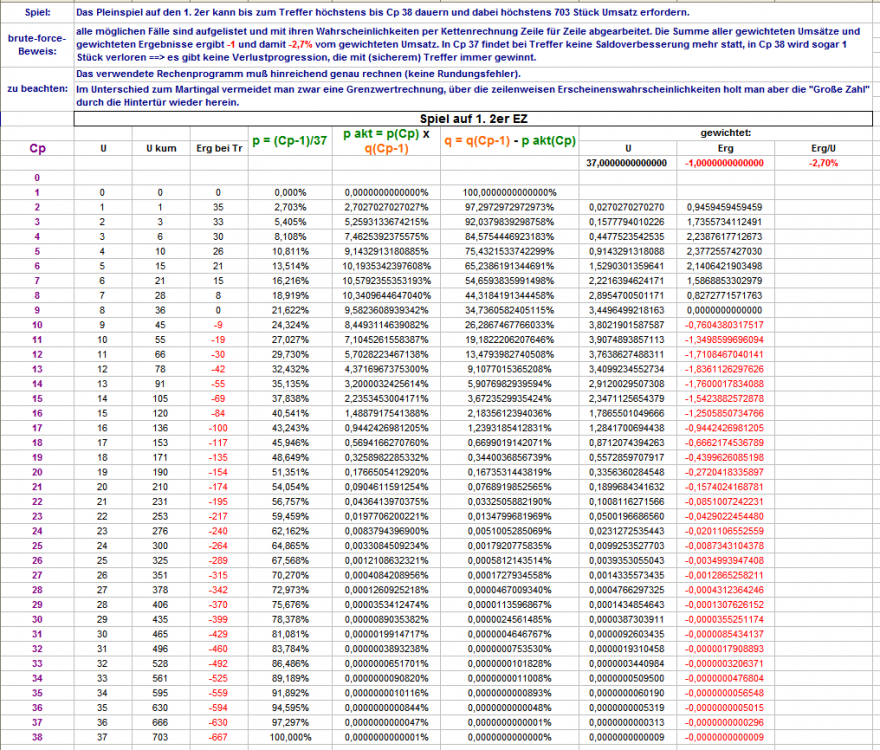
Im anderen Thema schildert @Optikus das scheinbare Paradoxon: https://www.roulette-forum.de/topic/7004-was-weiss-der-zufall/?page=8&tab=comments#comment-371708 Im Bereich winzigster Erscheinenswahrscheinlichkeiten läßt sich auch folgende, scheinbar widersprüchliche Überlegung machen. Beim Spiel auf den ersten Plein-Zweier ist das Spiel spätestens mit dem 38. Coup und Zwangstreffer beendet. Wie man aus der vollständigen Beschreibung ersehen kann: https://www.roulette-forum.de/uploads/monthly_2017_05/EZ_1._2er_bruteforceBeweis_01.png.966b0a462f7cf62baa7727c15ad7e5ac.png ist es unmöglich, auf dem Weg zum zwangsläufigen Treffer mehr als 703 Umsatzstücke zu verbraten. Könnte man nun zeigen, daß eine Einzelzahl länger als 703mal ausbleiben kann, hätte man einen Widerspruch insofern, als man dann sehr wohl Roulette "gut" oder "schlecht" spielen könnte. Nun, wohl an; schon mit "moderaten" 1/(1-1/37)^704=1/(36/37^704)=1/238.261.133 würden wir im Schnitt bei der Verfolgung einer beliebigen (auch von Coup zu Coup wechselnden) Einzelzahl mit 704 NichtTreffern am Stück rechnen können, und hätten damit 1 Stück mehr ausgegeben, als beim Spiel auf den ersten Plein-Zweier. Scheinergebnis: Man kann Roulette "schlecht" spielen. Richtiger Schluß aus Scheinergebnis: Wenn man Roulette "schlecht" spielen kann, dann muß es auch möglich sein Roulette "gut" zu spielen. Ha ha! Triumphgeheul, und pos. EW wir kommen! AUFLÖSUNG: Kommt es bei der Konstruktion eines Spiels mit Zwangstreffer in vorherbestimmbarer Zeit zu Satzbefehlen, die alle Erscheinensmöglichkeiten abdecken, ist die Sinnlosigkeit (und Banalität) eines solchen Tuns sofort offenbar. Beim Spiel auf den ersten Plein-Zweier und einem gewichteten Ergebnis von -1 auf 37 Stück Umsatz: solange es möglich ist, daß man 37 Zahlen setzen müßte (und selbstverständlich ist es möglich), könnte man sich den ganzen Aufwand der vorherigen Satzstufen sparen, und gleich einmal alle 37 Zahlen setzen, würde das eine Stück verlieren (hätte auch mit keinerlei Schwankungen zu kämpfen) - und fertig. Darüber wird nun überdeutlich: wir müssen (gewinn-)wirksam Erscheinensmöglichkeiten bestimmen, die wir nicht spielen. Und sind im Ergebnis genauso schlau, wie ein x-beliebiger Spieler der zum ersten Mal an den Roulettetisch tritt, und sich fragt wohin er sein Stück platzieren soll. Die wiederholte Frage von Otto, lange bevor er Ken mit Fritten foltert: "wie war das noch mal im Mittelteil?" umschreibt nicht nur im Film das Entscheidende. Ob nun beim Van-der-Waerden-Erklärbeispiel: falls es einen pos. EW zu finden gibt, muß er in der gewinnwirksamen Nutzbarmachung der Mehrfachsatzbefehle liegen; oder der Fx-jagd im anderen Thema, wo MarkP./Lexis schon vor langer Zeit sehr richtig und damit abschließend festgestellt hat: gewinnwirksam kann nur sein, die "guten" von den "schlechten" Favoriten zu unterscheiden; der Rest ist Budenzauber und Kulissenschieberei (keinerlei Schmähung damit beabsichtigt!), der zeitgebunden eine Weile gut geht mag. Gruß elementaar

Hallo wiensschlechtester, wie schade!; das wünscht man keinem und Du hast mein volles Mitgefühl. In Sachen Tabellenlöschung könnte vielleicht @Paroli behilflich sein. Aber für Deine aufgewendete Arbeit tut es mir leid. Je nach verwendeter Testapparatur sind vielleicht Teile noch rettbar, aber, wenn ich es richtig sehe, müssten von 69G die Cps 7, 8 und 9 betroffen, und damit die Daten infiziert sein. Schade, schade! Bis ich die Gegenfiguren in meinen Routinen komplett und fehlerfrei implementiert habe, wird es leider noch einige Zeit dauern - ad hoc kann ich Dir also mit Taten auch nicht zu Hilfe eilen. So bleibt die situativ nicht immer hilfreiche Plattitüde: "Fehler passieren halt" - aber danke für Deine Korrekturmeldung. Gruß elementaar

Nachgedacht habe ich darüber schon vielmals und seit langer Zeit, auch etliche Experimente gemacht - nur zu einer spruchreifen Lösung bin ich bis jetzt nicht gekommen. Das mag nun daran liegen, daß ich einfach zu doof und/oder vernagelt bin - oder es handelt sich, mal wieder, um ein Phänomen, welches zwar nachweisbar, aber zu schwach ist, gegen den neg EW anzukommen. Da ist zunächst die Methode (1) des Verkleinerns der Chancengröße (hier: 25er-EC-Figur, das kann man aber natürlich für jede Chance machen, bspw. Pleintriple, -quadrupel, oder Progressionsfolge u.ä.): @AlterSchwede hat es rechnerisch erwähnt, @Optikus hat es oben sehr gut erklärt; die erwartbaren Ergebnisse der Großen Zahl können sich gar nicht einstellen, mangels Masse an Ereignissen innerhalb eines Spielerlebens. Folglich "spart" man Bruchteile des rechnerischen Umsatzverlustes, weil einige Satzbefehle gar nicht praktisch umgesetzt werden können. Leider addieren sich diese Bruchteile (bei Millionen Möglichkeiten wird man mehr als eine innerhalb eines Spielerlebens nicht sehen) nur zu einer Gesamtwinzigkeit, die weit entfernt ist, den neg EW auch nur zu kompensieren. Bei Pleinquadrupeln (1/37^4 = 1/1.874.161) kam ich zwar regelmäßig auf Trefferquoten von um 2,71%, aber erstens reicht das bei weitem nicht, und zweitens sind diese statistischen Ergebnisse nicht aussagekräftig, weil sie innerhalb der natürlichen Schwankungen liegen. Und aus einem möglichen Blickwinkel gesehen, ähnelt das ganze Vorgehen natürlich Grilleau (vereinfachend: benutze außergewöhnliche (seltene) Erscheinungen für die Satzfindung), was aber den entscheidenden Nachteil hat, daß es für ein Dauerspiel nicht geeignet ist (noch vereinfachender: im Grunde ist es eine, gar nicht mal dumme, Streckung des Bold Play). Bei Methode (1) ist natürlich ein Nachteil, daß wir vorher nicht wissen können, welche spezifischen 25er-Figuren wir nie sehen werden. In Methode (2) fragt man sich, ob wir bestimmte Figuren mehrmals sehen werden (Ballungen). Man würde dann bspw. auf den 1. 2er der 25er-Figur spielen. Leider bin ich schon beim Versuch mir eine Binomialtabelle für die 15er-Figur (sic!)(1/2^15 = 1/32.768) zu errechnen (um sie nachfolgend mit der Statistik zu vergleichen) jämmerlich gescheitert. Landläufige Rechenprogramme geben das einfach nicht her. Und dennoch ist mir eine (leider begründungslose) Behauptung von @Haka im anderen Forum im Gedächtnis geblieben, der einmal schrieb, die errechneten binomialen Werte sollten sich mit Verkleinerung der Chancengröße immer genauer erfüllen. "Genauer" faßte ich damals als "mit geringeren Schwankungen zum Hochpunkt" auf, aber wer weiß, was er gemeint haben könnte. Wie oben schon erwähnt, bis zur einschließlich 17er-Figur bin ich statistisch gekommen - ohne Befund. Möglicherweise (bitte, mit ALLER Skepsis: möglicherweise!) gibt es noch eine Methode (3), wie man die Sache betrachten könnte: Sie ist mir in den Sinn gekommen, als ich beobachtete, wie sich mein Beispielmartingalist auf Dauer verhält. Beschrieben hier: https://www.roulette-forum.de/topic/18065-der-satz-von-van-der-waerden/?page=7&tab=comments#comment-359563 weiter kurz erläutert: https://www.roulette-forum.de/topic/18065-der-satz-von-van-der-waerden/?page=7&tab=comments#comment-359587 Klar ist, weil hier am häufigsten zu setzen ist, daß Einsatzspalte 1 (Satzhöhe 1 Stück) beim Dauerspiel am schnellsten in den Bereich der Großen Zahl gerät. Das setzt sich nach rechts mit steigender Satzdauer fort. Dies bedeutet nicht nur, daß in relativ kurzer Satzzeit in Spalte 1 nichts mehr zu verdienen ist, sondern auch, daß für ein positives Endergebnis die nachfolgenden Spalten zusätzlich zu ihrer eigenen, das kaum noch schwankende Umsatzminus von -1,35% aus Spalte 1 auszugleichen haben. Vielleicht interessant ist nun folgende Beobachtung: In frühen Satzstufen (wer hat noch keinen Martingalisten am Tischlimit (ca. 10x Verdoppeln des Einsatzes) scheitern gesehen) kommen größere NichtTreffersprünge (>10) praktisch jederzeit, und meistens viel zu früh, in späteren Satzstufen scheinen (!) die weiteren NichtTreffersprünge deutlich geglättet und nicht mehr so groß zu sein. So konnte ich nicht beobachten, daß bspw. das nach einem längsten Ausbleiber von 30 Sätzen innerhalb von 1.024 30er-Sätzen durchschnittlich ein 40er-Ausbleiber gekommen wäre. Paralell dazu erscheinen jedoch sämtliche Ausbleiber >20 z.T. beträchtlich früher als erwartbar. Dazu muß allerdings klar gesagt werden, daß selbst meine beobachteten 500 Milliarden Sätze für diese minimalen Erscheinenswahrscheinlichkeiten zu wenig sind. Die scheinbar am verstörendste Schlußfolgerung aus (3) ist jedoch: wirklich gewonnen werden kann (nicht muß!) klassisch nur am jeweiligen rechten Rand der Satzspalten. Was für den praktischen Spieler bedeutet: halte Dich mit Deinen Sätzen von der Großen Zahl fern (nichts wirklich Neues) und: mit steigender (Satz-)Zeit mußt du nach einem erzielten Treffer immer länger warten, bis dir mal wieder eine Satzmöglichkeit am rechten Rand präsentiert wird (der sich noch dazu immer weiter nach rechts verschiebt!). Sehr merkwürdig, und - falls es stimmt - was fangen wir damit an? Gruß elementaar

Hallo Hans Dampf, Und in wie weit beeinflußt die Absicht eines x-beliebigen Spielers, wie er die nächsten Coups zu spielen gedenkt, die Erscheinenswahrscheinlichkeiten? Oder, noch allgemeiner gefragt: in wie weit beeinflußt die Fähigkeit eines Spielers in vergangenen Coupsfolgen Muster zu erkennen und daraus Satzbefehle zu konstruieren, die Wahrscheinlichkeiten für das Ergebnis des nächsten Coups? So ist ja auch das scheinbare Paradoxon von Optikus sehr einfach aufzulösen: Die von ihm demonstrationsweise erblickte 25er-Rotserie hat korrekt eine Erscheinenswahrscheinlichkeit von 1/2^25 = 1/33.554.432. Und eine 30er-Rotserie hätte korrekt eine Erscheinenswahrscheinlichkeit von 1/2^30 = 1/1.073.741.824. Viel winziger - stimmt. Nur leider gibt es nur 2^5 = 32 Möglichkeiten, wie es in den nächsten 5 Coups weitergehen kann. - Mehr ist nicht drin. Die Milliarden Möglichkeiten der Vergangenheit schrumpfen für die Zukunft je nach gewünschter Spielstrecke gehörig zusammen. Und anders als es die Ruhlättcornifähre ständig posaunt: es ist nicht alles Meinung - es gibt auch noch nicht sinnvoll zu bestreitende Tatsachen (oder, ohne den alten, genauso sinnlosen Philosophenstreit befeuern zu wollen: eine Wirklichkeit außerhalb von uns selbst). Erst wenn Du nachweist, daß nach bestimmten 25er-Figuren die Erscheinenswahrscheinlichkeit bestimmter nachfolgender 5er-Figuren nicht mehr 1/32 ist, haben wir etwas, was zu diskutieren lohnt. Gruß elementaar

Hallo Hans Dampf, Hast Recht. Das ist natürlich der alles entscheidende Unterschied! Wo sind noch mal gleich die Indizien dafür veröffentlicht, daß die eine, so sorgfältig benahmte 27er-"Rot"-serie sich signifikant anders verhält als alle anderen aus 134.217.728 möglichen? Es macht halt Arbeit das nachzuprüfen. Ich selbst bin bis jetzt bis zur 17er-Figur gekommen - ohne Befund. Gruß elementaar

Entlarvend ist, daß regelmäßig das Beispiel mit den (diesmal) 27 ununterbrochenen Rotwiederholungen hervorgekramt wird. In wie fern zeichnet sich diese 27er-EC-Figur von allen anderen 2^27 = 134.217.728 (ohne Zéro) aus, außer daß diese eine (und die auf Schwarz) vom ganzen Spielsaal bemerkt wird? Durch nichts. Fällt 27 Coups lang Zéro nicht, hat man die nächste 27er-Serie aus 134.217.728 möglichen. Fällt im nächsten Coup wieder kein Zéro, hat man die nächste 27er-Serie aus 134.217.728 möglichen, und eine 28er-Serie aus dann 2^28 = 268.435.456 (ohne Zéro) möglichen usf. Mißt man die Abstände zwischen dem Erscheinen von Zéro, bekommt man eine Ahnung, wie lange xer-Figuren (2^350?; 2^600?; 2^beliebig?) werden können, und ungeachtet der Winzigkeit der Erscheinenswahrscheinlichkeit jeder einzelnen, diese eine ist gerade erschienen. Und das sagt uns: NICHTS! Man kann eben nicht beides zugleich haben: ist die Wahrscheinlichkeit im nächsten Coup für eine Zahl immer und überall p=1/37, dann darf man in Erscheinungen nichts hineingeheimnissen die, gerade weil p=1/37 ist, völlig normal = zufallsgerecht sind. Gruß elementaar