elementaar

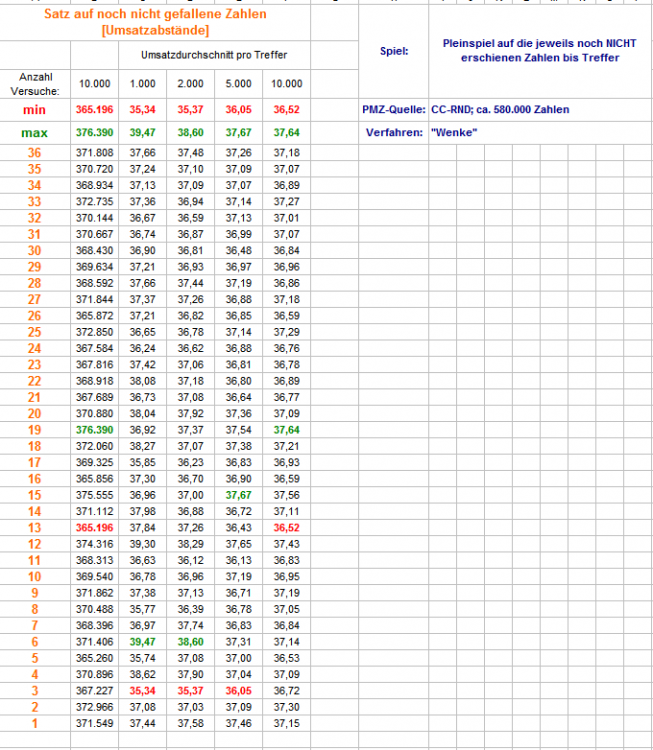
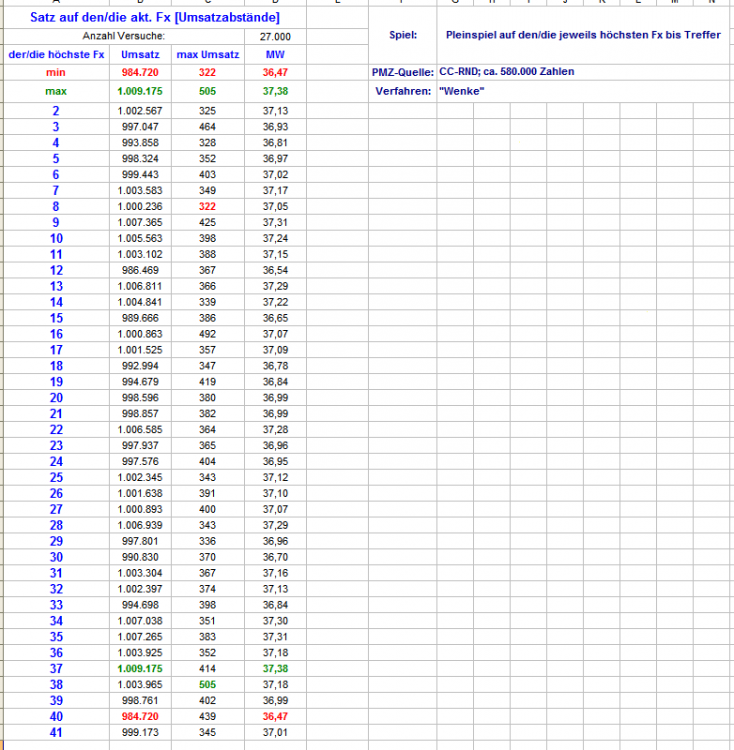
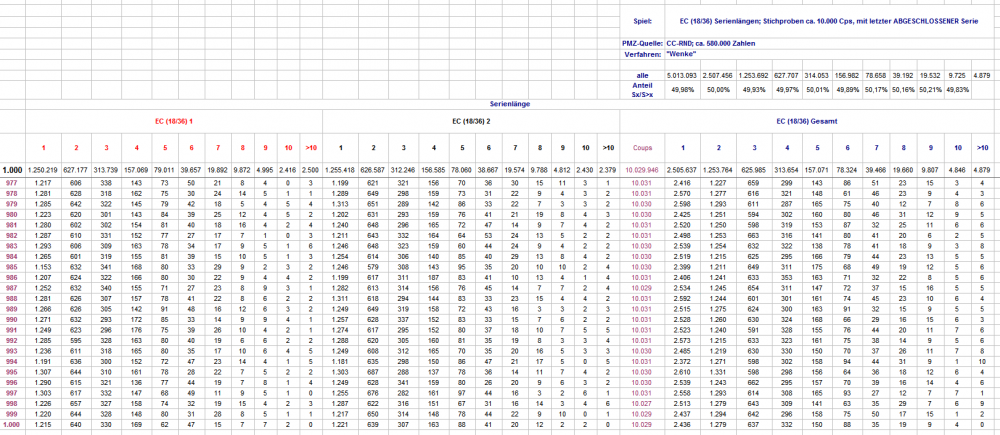
Hallo hemjo, als Lesehilfe der Tabellen zwei Beispiele: In der Tabelle der Ausbleiber die letzte noch nicht gefallene Zahl (letzte Zeile der Tabelle bezeichnet mit "1"): in dieser Stichprobe mußten nach 1.000 Versuchen durchschnittlich 37,44 Stücke bis zum Treffer aufgewendet werden. Nach weiteren 1.000 Versuchen (gesamt also 2.000 Versuche) war der durchschnittliche Stückverbrauch 37,58 bis zum Treffer usf. In der Favoritentabelle die Zeile bezeichnet mit "2": Es werden alle auftretenden 1er bis zum Treffer (=1. 2er) gespielt. Der dazu nötige Umsatz wird addiert. Geteilt durch die Anzahl der Versuche ergibt sich der durchschnittlich nötige Stückverbrauch (MW). Zum Treffen des jeweiligen 1. 2ers waren in dieser Stichprobe also durchschnittlich 37,13 Stücke nötig. Der von Dir vorgeschlagene Vergleich läßt sich machen, schöne Idee, ich bitte um etwas Geduld; allerdings muß auch der letzte Ausbleiber bis Treffer gespielt werden, sonst müßten zu viele Versuche gemacht werden, um die durch das Abschneiden der Permanenz verstärkten Schwankungen zu glätten. Gruß elementaar

Hallo Egoist, Hallo hemjo, selbstverständlich habt ihr recht. (Falls sich tatsächlich einer findet, der es bezweifelt!) Mit "Beweisen" im strengen Sinn ist es ja so eine Sache. Für spielpraktische Indizien bedarf es allerdings gar nicht so vieler Versuche. Als faktenbasierte Argumentationshilfe mag die folgende Auszählung dienen. Zunächst die ausgebliebenen Zahlen: Dann die Favoritenzahlen: Eine weitere Kommentierung sollte sich erübrigen. Gruß elementaar

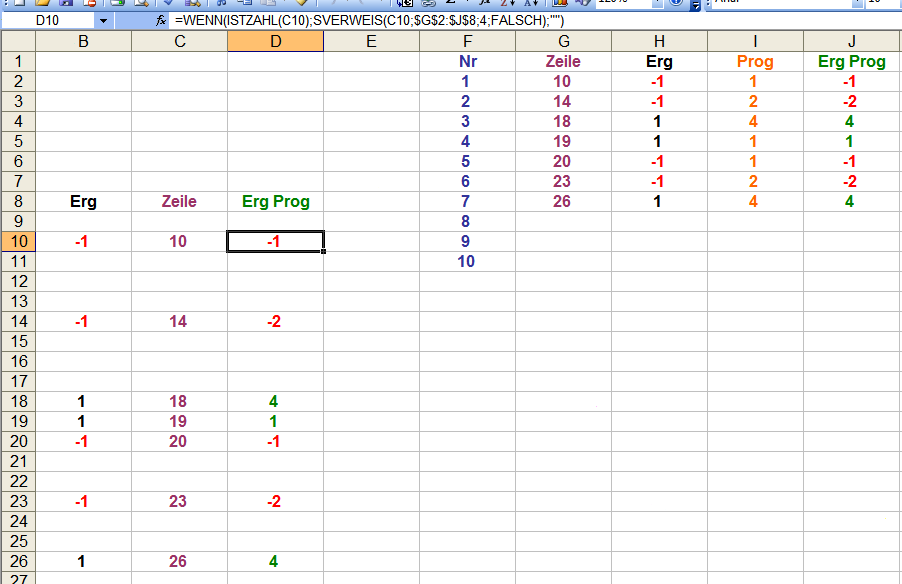
Hallo kesselman, bitte entschuldige, daß ich erst jetzt antworte; ich habe Deine Frage gerade erst gesehen. Deine Aufgabe läßt sich mit SVERWEIS() recht einfach lösen. Beispiel: Angenommen Deine Gleichsatzergebnisse stehen in Spalte B, die Zeilennummern in Spalte C und Deine Zusammenfassung In F2:J8. Für die Rückübertragung Deiner Progressionsergebnisse reservierst Du Spalte D Dann schreibst Du in bspw. Zelle D10: =WENN(ISTZAHL(C10);SVERWEIS(C10;$G$2:$J$8;4;FALSCH);"") und kopierst herunter. Die Progressionssatzhöhe könntest Du dementsprechend mit: =WENN(ISTZAHL(C10);SVERWEIS(C10;$G$2:$J$8;3;FALSCH);"") abbilden. Bezug innerhalb des Verweises ($G$2:$J$8) an Deine Gegebenheiten anpassen. Gruß elementaar

Hallo Dr. Manque, Verzeihung, da sei aber doch, in aller Höflichkeit, die Nachfrage gestattet: Deine (natürlich sehr sachliche) Feststellung(?) ad persona beruht noch mal auf welchen, nachprüfbaren Tatsachen? Drei bis fünf Belege würden als Indiz fürs Erste durchaus reichen. Und die strenge Sachlichkeit dieser Einleitung des "sachlichen, ehrlichen Bericht"(s) kannst Du noch mal wie und mühelos belegen? Oder gehört das, Deiner Meinung nach, auch wieder in den Bereich des Glaubens? Doch Vorsicht, mit Leuten, die überwiegend, oder auch nur fallweise, so wie es ihnen gerade passt, "glauben", kann man sich schlechterdings nicht sinnvoll unterhalten. Gruß elementaar

Hallo Starwind, Das ist nichts für mich. Sonderbar ist halt das Verhalten, erst die offensichtlich beutelschneiderischen Geschäftsbedingungen zu akzeptieren, und dann weitere Lebenszeit damit zu vergeuden, über evtl. stattfindenden Spielbetrug zu spekulieren. Ist es wirklich von Interesse, ob sie einen durch "falsche" Zahlen, Spielabbrüche, oder durch abstruse Auszahlungsbedingungen, oder noch bizarrere Sperrfristen ausnehmen, wo man doch vorsorglich in jegliches Ungemach, welches sie einem bereiten könnten, voll und ganz eingewilligt hat?! Ist aber nur ein weiteres menschliches Verhalten, das ich nicht nachvollziehen kann - und mich dabei auf bloßes Feststellen beschränken muß. Gruß elementaar

Hallo Dr. Manque, da über Glaubensdinge nicht diskutiert werden kann, bleibt nur die Schlußfolgerung: konsequenterweise mußt Du dann aber auch glauben, daß die geprüft veröffentlichten Auszahlungsquoten der angebotenen Spiele, welches Pflichtmitteilungen sind und teilweise in der Bilanz stehen, gefälscht sind; und/oder die Prüfbeamten bspw. im EU-Land Malta sämtlich korrupt. Wo geht das so ergaunerte Geld hin? Daß die Geschäftsbedingungen, denen der Spieler sich per Unterschrift zu unterwerfen hat, überwiegend ein Witz (d.h. die freiwillige Einwilligung in das eigene Beraubt werden) sind, muß man nicht glauben, sondern kann es Schwarz auf Weiß nachlesen und damit wissen. Gruß elementaar

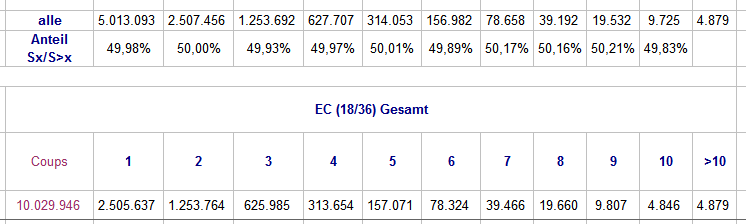
Hallo Stallinator, Aus der oben abgebildeten Tabelle der zusammenfassende Ausschnitt: In insgesamt 10.029.946 Cps konnten 5.013.093 Serien unterschiedlicher Länge gezählt werden. Serien der Länge 1 und 2 scheiden bei Deinem Spiel aus. Verbleiben 1.253.692 Serien der Länge >=3. Da man Serienlängen erst feststellen kann, wenn die betreffende Serie abbricht, bedeutet dies: 1.253.692 mal hättest Du ein Stück setzen müssen, in der Hoffnung aus der vorliegenden 3er-Serie werde irgendeine längere Serie. 625.985 hätte diese Hoffnung getrogen (Serienlänge genau 3), immerhin 627.707 mal hätte es geklappt (alle Serien >3). In dieser Auszählung wären also zu erzielen gewesen: 627.707 Treffer - 625.985 NichtTreffer = 1.722 Stücke Plus 1.253.692 / 1.722 = 0,14% vom Umsatz Das ist so mickrig, daß es mühelos innerhalb der natürlichen Schwankungen liegt. Für Serienlängen von 4 und >4; 5 und >5 usf. fallen die Ergebnisse ähnlich ernüchternd aus. Gegen Deine Progressionsgestaltung, und die Gründe dafür, gibt es auch nichts zu sagen - eher im Gegenteil. Und Deine Hoffnung ist ja auch nicht unbegründet. ALLERDINGS (und das könnte Dich schockieren): Bei einem Spiel ohne Trefferüberlegenheit ( pos EW) handelt es sich IMMER um ein Spiel auf Zeit; d.h. der Zeitpunkt des Platzers läßt sich nicht vorhersagen, daß er aber kommen wird ist sicher. Deshalb empfiehlt es sich bei jedem Spiel auf Zeit, sich möglichst eng an das sog. Bold Play (gesamtes Risikokapital einen Coup lang auf eine EC - danach NIE wieder spielen (wörtlich!); Erfolgswahrscheinlichkeit mit Zéro: 18/37 = 48,65% ) anzupassen. Das würde in Deinem Fall bedeuten: Risikokapital: 96 Stücke maximal Gewinn mit Bold Play: 96 Stücke per Progression: 50% davon = 48 Stücke. Danach: mindestens dieses Spiel NIE wieder spielen! Hier noch Links, wo ansatzweise erläutert wird, wie es zu der 50%-Beschränkung kommt (vorsichtige Spieler geben sich sogar mit 10 oder 20% zufrieden): https://www.roulette-forum.de/topic/18065-der-satz-von-van-der-waerden/?page=7&tab=comments#comment-359563 https://www.roulette-forum.de/topic/18065-der-satz-von-van-der-waerden/?page=7&tab=comments#comment-359587 Gruß elementaar

Hallo Stallinator, sehr erfreulich, daß Du Dir die Mühe gemacht hast, Deine Überlegung in einem Text zu schildern, der mehr ist als ein gestammelter Halbsatz. Mir zumindest fällt eine Unterhaltung so deutlich leichter, als das Prinzip "Raten per Schlagwortzuruf", vielen Dank dafür. Zu Deiner Überlegung: Selbstverständlich kann man das so machen, wie Du es schilderst. Jedoch ein paar Eingangsbemerkungen (ohne Zéroberücksichtigung) dazu: Was den Coupsverbrauch angeht ist das zwar richtig, per Kurzschluß läßt sich damit ein Trefferüberschuß aber nicht generieren. Unten findest Du das Ergebnis einer Auszählung zum Serienverhalten von EC (18/36), die, leider, belegt, daß das Verhältnis von Serienlänge x zu Serienlänge >x mit 50% gleich bleibt. Per Rechnung gibt es sogar einen winzigen Vorteil in Richtung jeweils kürzere Serienlänge (weil per Rechnung ein winzige Wahrscheinlichkeit einer bspw. >50er-Serie zwar existiert, sie sich jedoch kaum einmal materialisieren wird - aber auch damit läßt sich Zufallsgeschehen kaum austricksen). Auch diese Beobachtung entspricht durchaus der Wirklichkeit. Was aber kein Wunder, sondern nach egal welchem Vorlauf gegeben ist: Deine Spielsequenz entspricht einer 3er-Figur, von denen es acht Stück gibt. Dein erster Coup entspricht einem NichtTreffer der 3er-Figur (Abbruch Deiner Serie). Von den acht 3er-Figuren sind also vier ausgeschieden. Bleiben die anderen vier. Lediglich bei einer von vier (1/4) wirst Du nicht mindestens einen Treffer in den nächsten beiden Coups erblicken. In drei von vier Fällen (3/4) wirst Du umgekehrt mindestens einen Treffer verzeichnen können. So weit, so gut; -kann man machen, einen Trefferüberschuß sollte man damit allerdings auch nicht erwarten. Zu Deinem Progressionsvorschlag: Falls ich Dein Vorspiel richtig verstehe, streichst Du nach NichtTreffer - Treffer lediglich den letzten Fehlsatz. So etwas wie eine Stellentilgung findet also nur an den Übergangspunkten zur Satzerhöhung (alle drei Sätze) statt. Ob das reichen wird? Etwas irritiert mich Deine Platzerdefinition: 17 mal hintereinander verlieren mit p = 1/2^17 = 1/131.072 erscheint klein, aber 16 mal Nichttreffen mit nachfolgenden Treffer hinterläßt einen Saldo von -70 Stück und verschafft Dir eine Restspielstrecke zum Platzer von 2 Coups, was könnte damit gewonnen sein? Gruß elementaar

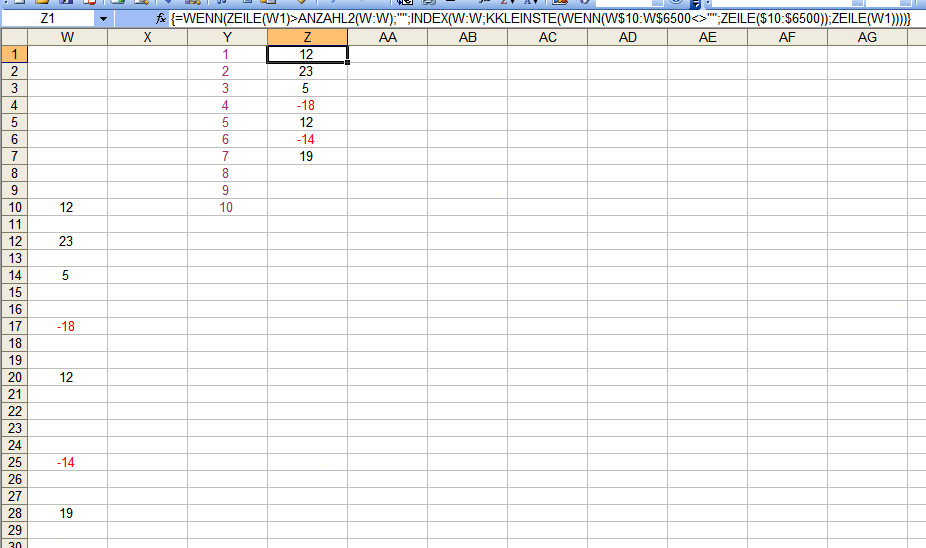
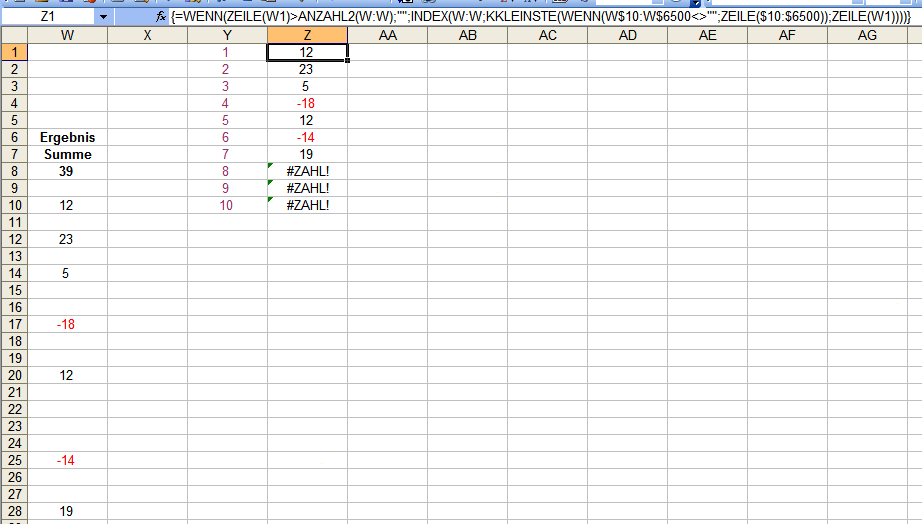
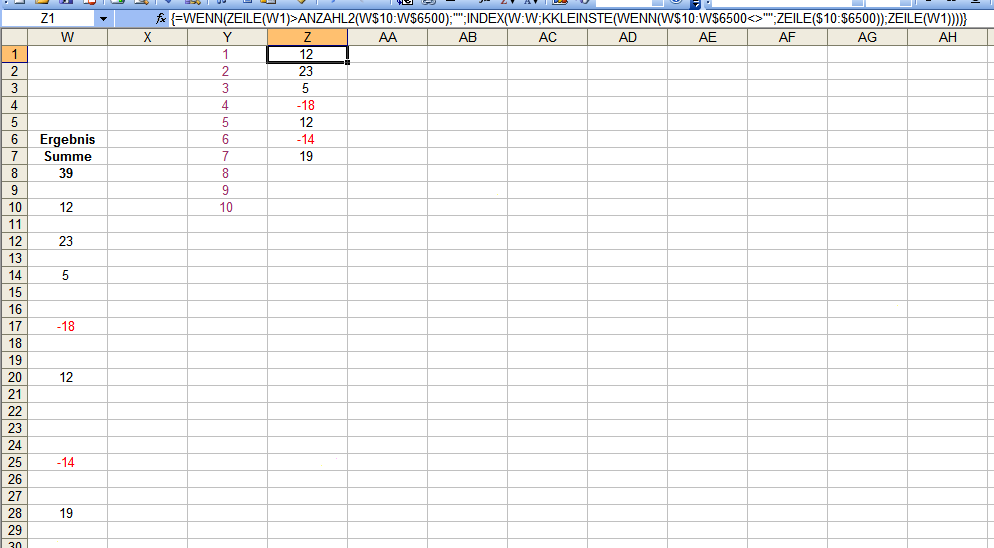
Hallo Samyganzprivat, wenn Du die Formel so =WENN(ZEILE(W1)>ANZAHL2(W:W);"";INDEX(W:W;KKLEINSTE(WENN(W$10:W$6500<>"";ZEILE($10:$6500));ZEILE(W1)))) änderst, wird es funktionieren (nicht vergessen unbedingt mit Strg+Shift (Hochstell)+Enter abschließen). Voraussetzung ist allerdings, daß die Zellen über Zelle W10 leer sind. Sonst erhälst Du bspw. ein solches Ergebnis: Mit dieser Abwandlung: =WENN(ZEILE(W1)>ANZAHL2(W$10:W$6500);"";INDEX(W:W;KKLEINSTE(WENN(W$10:W$6500<>"";ZEILE($10:$6500));ZEILE(W1)))) bekommst Du auch dies in den Griff. Gruß elementaar PS: Ich sehe gerade meine Antwort ist unvollständig; Pardon. Nach Abschluss der Formel in "Z1" mußt Du natürlich so weit wie gewünscht herunterkopieren (markierte Zelle rechts unten anfassen und herunterziehen), sonst erhältst Du ja nur die allererste Zahl aus Spalte "W".

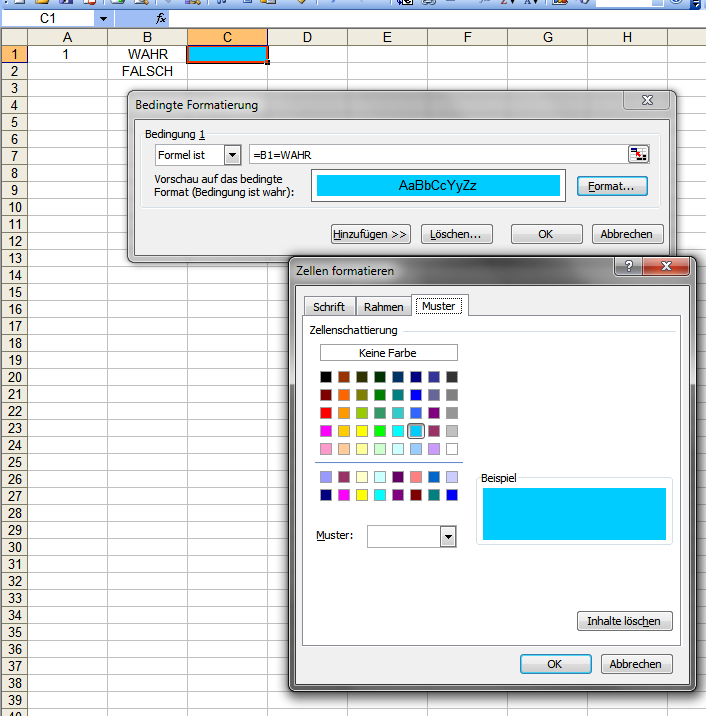
Hallo Samyganzprivat, zu 1: Beispiel: Angenommen in Zelle B1 steht als Formelergebnis WAHR und Zelle C1 soll sich dann Blau färben: Zelle C1 markieren; Format --> Bedingte Formatierung; "Formel ist" auswählen; ins daneben liegende Feld: =B1=WAHR schreiben "Format" wählen (rechts neben Vorschaufeld) im Reiter "Muster" die gewünschte Farbe per Klick wählen Mit "OK" abschließen. Die so bedingt formatierte Zelle so weit, wie gewünscht herunter kopieren. Siehe Bildschirmphoto: Gruß elementaar

Hallo Samyganzprivat, zu 2: per Holzhackermethode mit "INDIREKT": "Ich habe Spalten mit einer Länge von ca. 4000 Zeilen. Ungefähr in jede 100. Zeile steht eine Zahl (Tagesergebnis)" Beispiel: Angenommen Deine "Zahl" steht jeweils in Spalte C (C21 bis C4020), dann schreibst Du in Zelle D21: =WENN(ISTZAHL(C21);ZEILE();"") und kopierst dies bis C4020 herunter. In bspw. Spalte F schreibst Du untereinander die Zahlen 1 bis 50. In Zelle G1 (also neben F1 mit "1") schreibst Du: =WENN(ISTZAHL(KKLEINSTE($D$21:$D$4020;F1));KKLEINSTE($D$21:$D$4020;F1);"") und kopierst bis Zahl "50" (in F50) herunter. In Zelle H1 schreibst Du: =WENN(ISTZAHL(G1);INDIREKT("C"&G1);"") und kopierst bis Zahl "50" (in F50) herunter. Gruß elementaar PS: Der Vorschlag von @Revanchist leistet natürlich dasselbe - nur wesentlich eleganter durch weniger Zellen- und Formelverbrauch. Mein Vorschlag mag dazu dienen, die Logik der Revanchistenformel nachvollziehen zu können.

Hallo Ropro, im Anhang findest Du drei Beispiele für >30 verschiedene Zahlen in 37 Cps als .txt-Datei. Freut mich zu sehen, daß Du genauso profund weiter machst, wie Du begonnen hast. Sehr gut! Gruß elementaar Drei Beispiele für mehr als 30 verschiedene Zahlen in 37 Cps.txt

Hallo Ropro, das ist ja eine begeisternde Eröffnung! Ich bin geradezu entzückt: sehr gut vorbereitet und verständlich dargeboten. Perfekt. Dankeschön, Respekt und nur weiter so! Gruß elementaar

Hallo Shotgun, ich möchte die öffentliche Entwicklung Deines Gedankens gewiß nicht stören. Deshalb nur kurz: Ich habe Deine Eingangsfrage "was passiert..." wörtlich genommen, und eine neuerliche Auszählung der 6er-Figuren laufen lassen. Per Diagramm habe ich der chronologischen Entwicklung zugesehen; dabei fiel mir etwas auf. Als ich die jeweiligen Gegenfiguren mit ins Diagramm nahm, wurde es noch deutlicher. Deshalb sei mir gestattet, Dir schon jetzt vielmals Dank zu sagen: SO habe ich das bisher tatsächlich noch nicht gesehen. Ein (für mich) wirklich neuer Blickwinkel. Vielen herzlichen Dank! Wohin das führt, wird man sehen; umso gespannter bin ich auf Deine Fortsetzung. Nochmals vielen Dank! Gruß elementaar

Hallo Shotgun, prima, daß Du weiter machst - vielen Dank! Wenn ich es richtig sehe, stehen wir zur Zeit hier: Wir beobachten relativ kurze Sequenzen (kurz u.a. deshalb, um eine realistische Chance zu haben, deren Gegenteil noch zu unseren Lebzeiten erblicken zu können). Gemäß Nullsummenspiel in der Großen Zahl (wo die Schwankungen prozentual kaum eine Rolle spielen), werden wir zu jeder bspw. Sechs-Trefferfolge die entsprechende Sechs-NichtTrefferfolge erleben, und umgekehrt. Jetzt bin ich gespannt, wie Deine Überlegung weiter geht - und versage mir jegliches Spekulieren. Gruß elementaar

Hallo Ropro, So wie Du es schilderst, kann man es natürlich machen. Wenn ich @Shotgun allerdings wenigstens in diesem Punkt richtig verstanden habe, ist dies gar nicht die Frage (siehe seine Alternative mit d'Alembert). Ich möchte einfach nur möglichst präzise wissen, was wir denn "ein paar Tausend Coups" machen sollen, um, vielleicht, eine Antwort auf seine Frage "was passiert, wenn man immer die gleiche kurze Progression spielt" zu finden. Seine Angaben zur Versuchsanordnung sind ,leider, wie geschildert mehrdeutig. Gruß elementaar

Hallo Shotgun, freut mich sehr, und vielen Dank, daß Du Dich der Mühe unterziehst und den Versuch unternimmst, in diesem Forum einen sachbezogenen Beitrag einzustellen. Deine Kernaussage ist also: Es gibt etwas zu entdecken, was wir bisher so nicht gesehen haben. Nun gut, wenn es etwas zu entdecken gibt, will ich gerne dabei sein. Hoffentlich hast Du recht. Zu Deiner Frage: habe ich gleich Präzisierungswünsche, denn so unschuldig wie sie daher kommt, ist sie leider nicht. Denn schon hier: frage ich mich, was genau denn betrachtet werden soll, denn Deine Angaben können, mindestens, heißen: 1. es soll immer dieselbe Satzhöhensequenz gespielt werden, unabhängig ob Treffer oder NichtTreffer. Im Falle der Fibonacci wird also der jeweils 1. Satz mit 1 Stück gesetzt, 2. Satz mit 1 Stück gesetzt, 3. Satz mit 2 Stück gesetzt, 4. Satz mit 3 Stück gesetzt, 5. Satz mit 5 Stück gesetzt, 6. Satz mit 8 Stück gesetzt. Das ist dann ein Spiel mit 6er-Figuren (unterschiedlicher Satzhöhen) und damit ein Nullsummenspiel. 2. Nach jedem Treffer beginnt eine neue Sequenz; der 2. Satz tilgt 1 NichtTreffer, ab dann werden die 2 vorangegangenen NichtTreffer getilgt. 6 NichtTreffer in Folge kosten 20 Stück, und damit jeder dieser NichtTreffer rund 3,4 Stück. 3. Die Progression wird bis Saldo 0 oder 1, jedoch höchstens bis zum Verlust der höchsten Stufe gespielt. Weitere Varianten sind denkbar, falls man die Satzhöhen als Gewinnprogression auffaßt. Für einen Fingerzeig, was nun gemeint sei, wäre ich dankbar. Gruß elementaar

Hallo @starwind, Hallo @chris161109, danke an Euch beide für die sehr klare und schöne Darstellung! Besser kann man es nicht machen. Gruß elementaar

Hallo FavRad, Was für eine ausgezeichnete Idee! Glückwunsch, wäre schön, wenn unser Reservat ein paar ununterbrochene, sachdienliche Worte ermöglichte. Und @Ropro macht auch schon mit. Prima! Genau! Wenn, und falls!, das grundlegende Axiom jeder Wahrscheinlichkeitsrechnung gilt: Aus einer Menge gleichartiger n gilt zu jeder Zeit die Erscheinenswahrscheinlichkeit für ein Einzelereignis aus n: p = 1/n. Dabei erfüllt sich die Forderung "zu jeder Zeit" hierbei nur, wenn eine genügend große Anzahl an Versuchen ("Große Zahl") vorliegt, und streng nur im Unendlichen. Die Tatsache, daß wir in der Vergangenheit lokal immer Ballungen und Ausbleiber sehen, berechtigt dann aber gerade nicht zu dem Schluß, wir könnten diese vor oder während ihres Entstehens genügend genau vorhersehen. U. a. @Hans Dampf hat schon mehrfach darauf hingewiesen: bloß weil eine Zahl (lokal) noch nicht erschienen ist, bedeutet das nicht, daß sie nicht mitspielt (und sich damit die Erscheinenswahrscheinlichkeit der anderen erhöht). All die Massenauswertungen der Vergangenheit (auch meine eigenen) haben deshalb immer nur ergeben: jede Chancengröße erscheint genau so oft wie ihr rechnerisch zusteht. In diesem Punkt wird das (mathematische) Axiom also durch die (statistische) Realität voll bestätigt. Und das gilt auch, wenn man die einfachsten wie kompliziertesten Spielanweisungen mit der Großen Zahl konfrontiert. Ob nun das Geschehen nach dem 1. 10er EZ, die Frage, was ist nach 20x Rot in Folge (=20er-Figur) zu erwarten, IRGENDEIN Spiel, was auf sein Verhalten nach +/- 3 oder auch 6 Sigma beobachtet wird, @Ropro hat es richtig beschrieben: die Bedeutung der Vergangenheit in diesen Auszählungen für den nächsten Coup ist fast 0. Ein Ansatz ist nun die Frage, ob es möglich ist, diese Winzigkeiten >0 mit irgendwelchen Tricks so zu verstärken, daß man spielpraktisch etwas damit anfangen kann. Antwort, für mich, noch offen. Vielleicht entsinnst Du Dich noch der drei "kritischen" Punkte, die ich in Dein Saldoverlaufsdiagramm der 1. 10er gemalt habe. Deine weitere Auswertung scheint meine Prognosen zu bestätigen (das ist immer schön, aber:) bloß in diesem einen Fall! Jedenfalls sind wir damit bei dem sehr weiten Feld der "Tendenz". Die "reine" Lehre würde nahelegen, daß die Irrtümer bei solcherart visueller Prognose in der Summe genauso teuer sind, wie die Gewinne aus den richtigen Vorhersagen (Ohne Hausvorteil). Eine Möglichkeit der Großen Zahl zu entgehen, bestünde vielleicht darin, eine Prognosesituation, die sich als richtig erwiesen hat, künftig nicht mehr anzuwenden (hat ihr Geld verdient). Fragt sich nur, was mit den falschen anfangen? Antwort, für mich, ebensfalls noch offen. Bitte entschuldige die äußerst rudimentäre Form des Eingehens auf Deinen Beitrag, im Moment ist meine Zeitnot einfach zu groß. Gruß elementaar

Schade, @ratzfatz, daß Du offensichtlich nicht in der Lage bist, die richtigen Sinnzusammenhänge zu erfassen. Für jemanden, der 90% der Beiträge der Ruhlättcornifähre für die reine Wahrheit hält, ist das allerdings auch, nicht erstaunlich, schwer. In wie weit Pöbelei und offene Mordlust (siehe Winkels Schädel) dieses, Dein Problem lösen sollen, ist nicht sogleich erfindlich. Weil irgendwann gar niemand mehr da ist, der in der Lage wäre, den Glauben an die eigene, allumfassende Wirkmächtigkeit und Großartigkeit zu erschüttern? Das ist so läppisch, daß sich eine Diskussion darüber von selbst verbietet. Schäbigste menschliche Niedertracht halt.

Unfaßbar! Selbst für die sich täglich selbst für jeglichen mitmenschlichen Umgang disqualifizierende Ruhlättcornifähre ein neuer, und kaum noch zu unterbietender Tiefpunkt an schäbiger Niedertracht. Tägliche Opfer von Lüge, Denunziation, Diebstahl, Raub, Vergewaltigung und Mord. ca. 1 Million mutwillig hingemetzelter Afrikaner in Ruanda; von Ruandern ca. 1 Million zu Tode gefolterte Vietnamesen; von Vietnamesen ca. 6 Millionen verstümmelte und ermordete Afrikaner in Belgisch Kongo; von Belgiern ca. 6 Millionen beraubte und dann ermordete Europäer; von Deutschen ca. 100 Millionen ermordeter oder planvoll verhungerter Sowjetbürger; von Sowjetbürgern Die Liste ist längst nicht vollständig. Aber da stellt sich ein außer Rand und Band geratenes Männlein in einem Rouletteforum im Jahre 2017 hin, und dekretiert, sie alle seien wohl nicht ganz unschuldig an ihrem Schicksal! "Soviel kann ich gar nicht essen, wie ich kotzen möchte" Max Liebermann zugeschriebener Ausspruch, angesichts der Naziseuche

Hallo donau, Dein vorläufiges Fazit ist schon erstaunlich und in seiner Absurdität schon ein ganz klein bißchen bizarr: Du stellst eine Frage und machst ungenügende Datenangaben; eine Frage zumal, die schon x-mal allein in diesem Forum mehr oder minder kompetent beantwortet wurde ( als unvollständige Auswahl, suche mal nach Beiträgen von @Optimierer; @Wenke; @Stern; @NoHazard; @PinkEvilMonkey; selbst von mir könntest Du einige passende Beiträge finden). Auf Deine Frage (die in der gestellten Form, den Verdacht auf enorme Faulheit im Recherchieren aufkommen läßt) erhälst Du nicht den erwartbar mißgelaunten Einzeiler, sondern mindestens drei Leute geben sich sogar Mühe, Dir im (notwendig) verkürzten Schnelldurchgang praktische Hinweise zu geben, damit Du mit Deinem Projekt weiterkommst. Die Antworten sind Dir nicht genehm? Sie machen zuviel Arbeit? Sie erfordern ein Minimum an eigener geistiger Verständnisleistung? Oder wenigistens das erkennbare Bemühen darum? Obwohl mehrfach darauf hingewiesen, sprichst Du weiter von "Rechenfehler", wo doch von Datenerfassung die Rede ist (wo nichts gerechnet wird!)? Das alles ist Deine Sache - ganz wie es Dir gefällt. Dein Fazit allerdings ist nicht nur eindeutig FALSCH, sondern auch dreist. Was Du mit Deiner Frage bezweckt hast, ist mir unerfindlich; das Erhalten einer halbwegs kompetenten, und praktisch anwendbaren Antwort war es ja offensichtlich nicht. @relieves hat es auf den Punkt gebracht: am besten folgst Du seinem Ratschlag, da brauchst Du weder Deine noch unsere Zeit zu verschwenden. Gruß elementaar

Hallo donau, Du kannst natürlich rechnen, was Dir beliebt - allein der Erkenntnisgewinn bleibt bei mancher, selbst formal, richtigen Rechnung auf der Strecke. Da ist zunächst das Problem, daß Du anfängst mit Durchschnittsgrößen zu rechnen. Das ist bei Zufallsgeschehen hochproblematisch, und wenn Du nicht ganz genau weißt, was Du tust, und was die daraus gewonnenen Ergebnisse bedeuten - und vor allem was sie NICHT bedeuten, kann ich Dir nur dringend raten, das zunächst mal sein zu lassen. Zumal ich aus Deiner Eingangsfrage herausgelesen habe, daß Du in der Phase der Datenerfassung bist. Da wird aber nichts gerechnet, sondern nur penibel sorgfältig (und ohne Selbstbetrug - alles weitere bezieht sich ja auf diese Daten, deshalb muß ihre Richtigkeit sichergestellt sein!) Satz für Satz aufgezeichnet, bei EC "+" oder "-", besser "Treffer" und "NichtTreffer". Wenn Du drei EC-Paare gleichzeitig auswerten möchtest, brauchst Du drei Spalten (Für jede EC eine), in die Du Deine Treffer/NichtTreffer Satz für Satz untereinander einträgst. In meinem obigen Beispiel über sinnvolle Stichprobengrößen ist natürlich gemeint, daß man von jeder Stichprobe mehrere braucht, sonst kann man keine belastbaren Aussagen treffen. Je nach vermuteter oder erhoffter Umsatzrendite (Faustregel: je höher die Umsatzrendite, desto weniger "muß" man testen), für mein Beispiel mit 10% Umsatzrendite würde ich 10 mal die jeweilige Stichprobengröße für ein Minimum halten. Praktisch also: Nach 100 Sätzen hast Du die erste 100er-Stichprobe beisammen, Treffer summieren, gesondert aufschreiben, neues Päckchen anfangen, nach weiteren 100 Sätzen wieder summieren usf. Hast Du das insgesamt 10 mal gemacht, hast Du auch gleichzeitig Dein erstes 1.000er Päckchen beisammen, Treffer summieren, gesondert aufschreiben etc. Falls Du nun bei ca. 50 x 100er-Stichprobe = 5 x 1.000er-Stichprobe = 1 x 3.700er-Stichprobe, Rest 1.300 Datensätze, auf durchgehend (in jedem einzelnen Päckchen!) kaum schwankende Umsatzrenditen von 10% kommst, hast Du entweder den heiligen Gral entdeckt, und, dadurch beflügelt, sollten die restlichen 32.000 Datensätze für die 10 x 3.700er-Stichproben ein Klacks sein; SEHR viel wahrscheinlicher ist jedoch ein Fehler in der Datenerhebung, und den solltest Du dann finden, bevor Du noch mal von vorne beginnst. Ich hoffe, das Prinzip ist klar geworden: bist Du bspw. nach 3.700 Sätzen saldopositiv, kannst Du jederzeit über die stufenweise kleineren Stichproben erkennen, was auf dem Weg dorthin geschah. Und schneller Deine Schlüsse ziehen. Als letztes (unwahrscheinliches) Beispiel: Nehmen wir an, nach 10 x 100 Sätzen, könntest Du Dir in der so entstandenen 1.000er-Stichprobe ein Saldoplus von 100 Stücken anschreiben, ABER 7 von 10 100er-Stichproben hätten ein deutliches Minus ergeben und lediglich eine Stichprobe hätte durch ein überragendes Plus alles rausgerissen, da würde bei mir die erste Warnlampe angehen; Erst wenn einige weitere 1.000er-Stichproben sich ähnlich verhielten, könnte man anfangen, über einen evtl. vorhandenen speziellen Charakter dieses Spiels zu spekulieren. Gruß elementaar

Hallo donau, "Experte" bin ich zwar bestenfalls im Nichtwissen, aber das peinlich genaue Einhalten der Anmerkung von @sachse ist Grundvoraussetzung für jedes weitere Vorgehen. Ergänzend zum Vorschlag von PinkEvilMonkey, dessen "allerwichtigstes" Du ebenfalls sehr strikt beherzigen solltest: PinkEvilMonkeys Angaben beziehen sich natürlich auf Gleichsatzspiel (1 Stück pro Satz) und jeweils nur ein gleichzeitig gespieltes Chancenpaar (bspw. Rot/Schwarz ODER Impair/Pair ODER Manque/Passe). Einfach nur 50.000 Sätze untereinander zu schreiben, ist dabei sehr ineffektiv. Sehr viel aussagekräftiger ist es, die Spieldaten in handlichere Portionen zu teilen. Deren brauchbare Größe bestimmst Du über den erhofften positiven Erwartungswert. Beispiel: Du erhoffst Dir 10% Umsatzrendite bei Deinem EC-Spiel (p=18/37) Bei einer Portionsgröße von 100 Sätzen werden alle Stichproben bis zu -1 Sigma noch saldopositiv sein 1.000 Sätzen werden alle Stichproben bis zu -3 Sigma noch saldopositiv sein 3.700 Sätzen werden alle Stichproben bis zu -6 Sigma noch saldopositiv sein Damit kannst Du, u. U sehr viel, schneller beurteilen, was passieren kann, und ob Deine Renditehoffnung im Bereich des real Möglichen liegt. Gruß elementaar

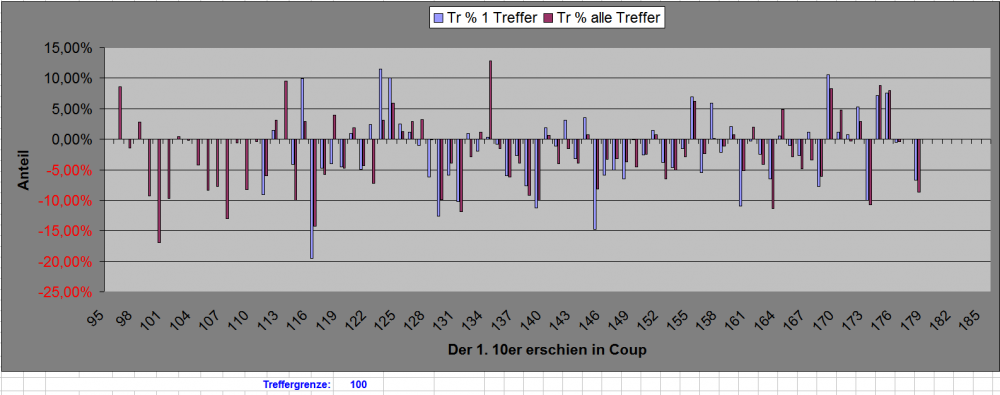
Hallo FavRad, unten siehst Du, was passiert, wenn man Deinen Prüfvorschlag mit RND-Zahlen ("bester" Zufall "tadelloser Qualitätsbeschaffenheit") durchgeht. Die summierten Ergebnisse beziehen sich auf zwei Varianten: einmal genau, wie von Dir beschrieben (Abwarten des 1. 10ers; dann Spiel auf einen Treffer, Abbruch sofort danach; benannt mit "1 Treffer"), einmal mit Weiterspielen selbst mit Treffer bis Coup 185; benannt mit "alle Treffer". Beide Male begrenzt auf die maximale Spielstrecke von 185 Coups (5 Pleinrotationen). Um nun zeitgleich die von Dir gemachten Beobachtungen über evtle Ergebnisauswirkungen in Abhängigkeit zum Erscheinenszeitpunkt des 1. 10ers untersuchen zu können, habe ich diesmal Umsatz, Trefferanzahl und Ergebnis lediglich als Gesamtergebnis summiert, und dafür aufgeschlüsselt aufzeichnen lassen, was nach jedem Erscheinenszeitpunkt des 1. 10ers geschieht. Damit man in dem Diagramm überhaupt noch etwas zu erkennen vermag, sind die Trefferquoten in [%] aufgetragen (3% Trefferquote mit EZ bedeuten (ohne Tronc) 8% Ergebnisplus vom Umsatz). Außerdem sind lediglich Startpunkte verzeichnet, die mindestens 100 Treffer erzielen konnten (Treffergrenze). Die natürlichen Schwankungen sind aber auch damit noch hoch. Gruß elementaar