elementaar

Hallo Albatros, Ganz so weit zu gehen ist nun, vielleicht, doch nicht nötig. Dein Beispiel 2 + 3 = 5 heißt schlichtweg "Rechnen", weil es hier darum geht, eine allgemeingültige Rechenvorschrift der Addition ("Mathematik") mit konkreten Werten zu befüllen ("2" und "3") und zu einem korrekten Ergebnis zu kommen. Und in meinen Volksschulzeiten hieß das betreffende Fach auch noch richtigerweise "Rechnen". Genau das wurde gelehrt und mehr oder minder richtig praktiziert. Heute treiben Erstklässler angeblich und großspurig aber falsch betitelt "Mathematik". Aber woher wissen wir denn, daß die Rechenvorschrift bei der Addition so und nicht anders ist? Und woher das Zutrauen, daß, wenn wir der Rechenvorschrift "Addition" folgen, wann immer wir sie korrekt anwenden, dann auch ein korrektes Ergebnis erhalten? Bei "2" und "3" Äpfeln können wir ja noch physisch nachzählen und sehen, ob die Rechnung stimmt, wie sieht dies aber bei Neutrinos aus? Oder bei sehr großen oder sehr kleinen Anzahlen von Irgendwas? Und wie ist es, wenn wir ganze Vorgänge (die Ergebnisse von ausladenden Rechnungen, Prozessabläufe usf.) addieren? Gelten dann dieselben Vorschriften? Gewiß: das auch von Dir hervorgehobene Wort "NICHTS" ist eine (kleine) Übertreibung, in dem Sinne: in der Mathematik wird ab und zu auch gerechnet. Aber bloß zu einem verschwindend geringen Teil. Eine deshalb zunächst flapsig wirkende Antwort auf die Frage, "wann ist es Mathematik", wäre: je abstrakter (und damit allgemeingültiger), umso mehr ist es "Mathematik". Also: 2 Äpfel + 3 Äpfel = 5 Äpfel oder: 2 Würstchen + 3 Würstchen = 5 Würstchen Das ist Rechnen. Nebenbei wird damit auch klar, daß es etwas wie: 2 Äpfel + 3 Würstchen = 5? was denn nun: Äpfel? Würstchen? nicht geben kann. Für einen Mathematiker sieht Dein Beispiel aber richtig so aus: 2x + 3x = 5x Aus praktischen Gründen wird das "x" als Variable oft nicht hingeschrieben, es ist aber immer noch da, und es wird mitgedacht. Die Marktfrau, die gerade 2 Äpfel und dann nochmal 3 Äpfel in eine Tüte zählt, belegt also in diesem Moment die Variable "x" mit der Art "Äpfel". Der Metzger, der gerade 2 Würstchen und dann nochmal 3 Würstchen auf ein Papierchen zählt, belegt in diesem Moment dieselbe Variable "x" mit der Art "Würstchen". Mathematisch "dürfen" sie das, weil sie in voneinander unabhängigen Gewerken unabhängig handeln. Die Additionsvorschrift gilt sowohl für Marktfrauen wie für Metzger. Ein beides-zugleich-Verkäufer darf dies jedoch so nicht machen. Er muß "Äpfel" mit der Variablen "x" und "Würstchen" mit der weiteren Variablen "y" belegen, sonst geht es mit seinem Geschäft sehr bald schief. Die Additionsvorschrift gilt auch für ihn, er muß aber streng beachten, daß er die eine "Art" nur mit derselben "Art" addieren darf. Das mag sich nun, zumal für diesen alltäglichen Vorgang, unglaublich umständlich lesen, ist aber genau das, was mathematisch hier geschieht. Das eigentliche Zusammenzählen ("rechnen"), beim Verkauf ("Geld" = Variable "z") sowohl für Marktfrau wie Metzger essentiell, ist für den Mathematiker eine Marginalie, er interessiert sich für das, was, wie oben beschrieben, abstrakt passiert, und versucht dieses Geschehen per allgemeingültiger Formel zu beschreiben. Im Falle der Addition ist dies schon vor Jahrtausenden allgemeingültig gelungen. Den Mathematiker interessiert das hinfort nicht mehr, diese Fragestellung ist ja erschöpfend und befriedigend gelöst. Rechnen (und damit die gefundenen Vorschriften ("Formeln") anwenden, selbst wenn ihnen das gar nicht bewußt ist!) tun dann andere (die dies, womöglich, viel routinierter und auch besser können). Mathematiker "erfinden" (und beweisen ihre Richtigkeit) Formeln, Rechner setzen bloß konkrete Werte in die Formeln ein und berechnen das Ergebnis. Ich will nicht gerade sagen, letzeres könne auch von einem begabten Schafswollpullover geleistet werden, aber in diese Richtung geht es. Vor einiger Zeit, vielleicht ist es Dir ja vor Augen gekommen, habe ich hier das Modell der Kettenrechnung erklärt, und dabei nicht nur geschildert wie, sondern auch warum man das so und nicht anders macht. Wenn Du so willst, das war "Mathematik", was bei der praktischen Rechnung herauskommt, ist bloß das Ergebnis von "Rechnen", vielleicht wichtig für den Spieler, klar, aber mathematisch von sehr weit untergeordnetem Interesse. Eine mathematisch interessante Aufgabe wäre hingegen, eine allgemeingültige Formel zu entwickeln, mit der sich zu jedem Spielzeitpunkt die kumulierte Wahrscheinlichkeit ohne Kettenrechnung bestimmen ließe. Mathematik ist es dann aber auch, abstrakt nämlich, sehr schnell zu begreifen, daß es eine solche Formel bei von Coup zu Coup anderen Trefferwahrscheinlichkeiten nicht geben kann, man sich also jegliches Nachdenken (bevor man überhaupt rumrechnet!) in dieser Hinsicht sparen kann. Der PC ("Rechner") mit dem ich dies schreibe, "rechnet" fast pausenlos und meist fehlerfrei, und dennoch käme es mir absurd vor, ihn "Mathematiker" zu nennen, dafür fehlt ihm so ungefähr alles, was einen Mathematiker ausmacht - wie u.a. Abstraktionsvermögen und Einsicht. Falls ich den Unterschied nicht verständlich genug beschrieben habe, zögere bitte nicht, nachzufragen. Ich wollte den Text möglichst knapp halten. Gruß elementaar

Hallo Albatros, Mathematik ist die exakteste Wissenschaft, die wir haben - so weit so gut. Was aber nicht heißt, daß es nicht auch in der Mathematik Bereiche mit gehöriger Unschärfe gibt (z. B. unterschiedliche Arten von "unendlich"). Im aktuellen Thema spielt das aber wahrlich keine Rolle. Wenn überhaupt, dann aber nicht über Mathematik (dazu fehlt uns beiden die Kompetenz) oder Rechenergebnisse, denn die waren ja weitgehend identisch. Es wäre schade, wenn das so angekommen ist. Auch das Wort "streiten" möchte ich, halten zu Gnaden, bestreiten, denn dafür bräuchte es mindestens zwei. Es begann mit einer bloßen Diskussion, und die kann, und manchmal muß, auch mal härter geführt werden, was ja noch kein Streit ist, sondern bloßes Ringen um klarere Sicht. Dann regte sich Egoist über irgend etwas auf. Weder meine wiederholten Versuche die Ursache dafür herauszufinden, noch der Vermittlungsversuch von Feuerstein, erbrachten jedoch Klarheit. Als er dann so außer sich geriet, daß seine Texte überwiegend Schmähungen ad persona enthielten, war halt meine persönliche Gesprächsausschlußgrenze erreicht. Er hat das auch früher schon mit anderen in diesem Forum gemacht, insofern nicht überraschend, für mich ist allerdings ein solches Verhalten nicht tolerabel und führt zum sofortigen Gesprächsabbruch. Mit Rechnen oder gar Mathematik hatte das aber wirklich nichts zu tun. Und dieses Thema im Übrigen auch nicht. Die Frage: 1/37 x 1/37 = 0,00073045; Kehrwert: 1.369 hat Ropro doch schon längst beantwortet. Auf den restlichen sechs Seiten stellen einige andere halt die "Güte" ihrer "Expertise" ins öffentliche Schaufenster, und blamieren sich dabei nach Kräften, so gut sie eben können. Bloß weil sich jemand zu einem Thema äußert, wird er dadurch ja noch nicht themenkompetent. Gruss elementaar

Darin erkennt ER einen Widerspruch? Ernsthaft?! Putzig. Aber klar, diese vermaledeiten "weil"-Beziehungen, die haben's aber auch in sich. In SEINEM Phantasiereich der immerwährenden logischen Fehlschlüsse nicht zwangsweise leben zu müssen, ist jedenfalls schon mal ein Glück. Das widerlegt, oder, in gewisser Weise, bestätigt sogar Schopenhauers Ansicht über die Qualität dieses Universums.

Hallo hemjo, mit der Bitte um Entschuldigung: irrtümlich schrieb ich weiter oben Deinen Namen groß. Um in Sachen Freiheit des Wohinsetzens nicht mißverstanden zu werden (ich weiß, daß viele Menschen Freiheit und die damit verbundene Selbstverantwortung fürchten): ich meine das gar nicht despektierlich. Ein paar Beispiele: Im aktuellen Spiel befände ich mich in der ersten Spalte (26 mal 1 EZ), da fällt mir auf, daß in kurzer Zeit einige Zahlen doppelt kommen, warum nicht für eine Weile jede gefallene Zahl einmal nachspielen, selbst wenn der "Plan" ein anderer war? Bei Vorgänger-Nachfolger-Pärchen genauso. Oder mir fällt auf, daß in Coup 10 schon der erste F4 gefallen ist, warum denn nicht setzender Weise auf ein erneutes Erscheinen hoffen? Oder, man befände sich in Spalte 5 (5 mal 5 EZ), warum denn nicht mal nachschauen, ob sich bei den Zahl-2-2-Sektoren etwas tut, wozu einem etwas einfällt? Das alles kann man ohne besonderes Risiko machen. Und man sollte es auch, um sich die Möglichkeit zu erhalten, von unverdientem Glück zu profitieren. Entscheidend sind immer die Ergebnisse des Setzens: nach jedem gefallenen Coup weiß man sicher, ob die eigene Prognose zum Treffer führte oder nicht. Stellt man dann fest, daß die eigenen Ideen zur Zeit zu viele NichtTreffer produzieren, muß man sich allerdings sehr konsequent und für eine ganze Weile von diesem Vorgehen verabschieden, und etwas anderes probieren, dann beispielsweise vorher festgelegte Zahlenfolgen spielen oder noch etwas anderes. Dieses geradezu manische Kleben mancher Spieler an einer Satzweise, die sich im Moment für diesen Permanenzabschnitt unmittelbar und faktenbewiesenermaßen (der Stückesack wird immer leerer) als untauglich erweist, habe ich schon immer als sehr sonderbar empfunden. Natürlich gibt es keinerlei Garantie, daß dann etwas anderes zum Treffer führt, aber wenigstens stoppt man damit das situativ eindeutig falsche Vorgehen. Und das kann man in der Satztabelle ja eindeutig ablesen: muß man ab Spalte 5 spielen, befindet man sich eindeutig am Rande des ungewöhnlichen Nichttreffens. Und dann gibt es noch den relativ einfach zu handhabenden Spezialfall: einfach jede Entscheidung führt in die NichtTrefferwüste; na dann auf, und die Möglichkeit, viele NichtTreffer möglichst billig einzukaufen, beherzt nutzen (siehe etliche Beiträge von @Egoist). Sich dem Zufallsgeschehen einfach passiv auszuliefern, führt mit Sicherheit zu den bekannten -2,7%. Ob es mit obigen Hinweisen auf Dauer anders läuft? Wahrscheinlich nicht. Muß es aber auch nicht, es muß lediglich bis zu unserem endgültigen Abschied von diesem Spiel halten. Gruß elementaar

Hallo Hans Dampf, da tanze ich mit, und sage, wenn ich es wüßte, würde ich es Dir sofort verraten, wenn's nur das wäre... Gerade bei EC ist es ja ein Leichtes, sich die herrlichsten Fehltrefferstrecken zu besorgen: das Gegenteil der letzten 60, 80, 100 gefallenen Coups, was immer man will - und sage keiner, das sei ja ganz unrealistisch, einer von 2^100 Spielern hat das ja schließlich, wie an der Ampel zu sehen, gerade fertig gebracht. Ich hoffe, ich verkünde nichts Neues: danach macht Zufall weiter wie immer und als sei nichts gewesen. Mal ein paar Stückchen Richtung "Ausgleich", mal noch tiefer in den Keller, vor allem aber, und das viel zu häufig, eine simple Seitwärtsbewegung mit Tendenz nach unten. Es ist aber auch ein Kreuz! Gruß elementaar

Naja, solange er halbwegs pari spielt, ist er natürlich für alle am Tronc-Beteiligten eine willkommene Quelle, ohne dem Haus zu schaden. Schleppt er allerdings öfters größere Summen ab, wäre es schon bedenklicher. Das muß dann aber vor meiner Zeit gewesen sein. Seinerzeit (1990er) spielte er Zahl-4-4 mit 200 oder 300 DM. Die Tischmannschaft muß schon eine Menge Pleinauszahlungen à 5 DM machen, um auf den Tronc bloß eines seiner Treffer zu kommen. Allerdings sah ich ihn auch in Mainz und Bad Homburg, und dort, für seine Verhältnisse, mit deutlich zivilisierteren Umgangsformen. Die Extrawürste in Saarbrücken waren zwar sehr ärgerlich, aber doch überwiegend kindischster Natur. Allerdings hat sich in Mainz auch einmal Prof. Laimbach, bei rapelvollem Haus, eine andere Kugel gewünscht, und sie auch bekommen. Was wirklich dahintersteckt, wüßte ich jedoch auch gerne. Gruß elementaar

Hallo Hans Dampf, das ist ja leider das Verflixte mit diesen Ausgleichsspielen. Schreibt man sich -36 Stück fiktiv an, hat man rechnerisch 36 Umsatzrotationen Zeit, bis ein (Teil)Ausgleich stattfinden könnte, dabei müßte der Ausgleich aber, je weiter die Umsatzzeit voranschreitet, umso umfassender sein. Je länger man diesem aber nachjagt, umso wahrscheinlicher wird es, daß er sich bloß prozentual einstellt, wovon man (geldbörsenmäßig) höchst selten etwas hat. Diese Art von Vergangenheit ist einfach nicht wirkungsmächtig genug, um nur den Hausvorteil zu egalisieren. Gruß elementaar

Hallo Hemjo, ich kann nur nochmals betonen: ich "rechne" möglichst wenig, und das aus einem einfachen Grund: jede Berechnung, sei sie richtig oder falsch (und die Wahrscheinlichkeit bei Zufallsgeschehen falsch zu rechnen, ist sehr hoch, siehe Raumfahrt- und Raketentechnik, Atomkraftwerke, Gesundheitsindustrie etc.), muß am Ende zwingend mit der Permanenzwirklichkeit konfrontiert werden, damit sie roulettespielpraktische Relevanz erlangt. Erst wenn die Auszählungen mal nicht den Erwartungswert ergeben, fange ich, vielleicht, mit dem Rechnen an; bisher immer mit dem Ergebnis, daß eine Fehlerkorrektur in der Auszählung gemacht werden mußte. Ich simuliere also Permanenzwirklichkeiten. Und da wäre ich, bei klassischem Spiel, doch außerordentlich erstaunt, wenn da auf Dauer, bei dieser Art von und fehlerfreier Auszählung, etwas anderes als der Erwartungswert heraus käme. Ich finde das eher beruhigend als zum Verzweifeln. Vielleicht ein paar Hinweise, wohin Du schauen könntest: 1. Zu jeder Chancengröße lassen sich Spielsequenzen herstellen, die in sich eine Erfolgswahrscheinlichkeit >50% haben (Figurenmodell bei EC, 1 EZ >= 26 mal setzen etc.). Das hat nicht nur den Vorteil, daß man, solange es klappt, mühelos Stücke einsammelt, viel wichtiger ist, daß die Sequenzen öfter und längere Plusserien bilden. 2. Zeichnest Du Dir die Graphen des Ergebnissaldos beliebiger Spiele mit beliebigen Chancengrößen für ein paar Tausend Sätze auf, wirst Du in praktisch jedem Graphen auch längere Phasen finden, wo es, relativ, aufwärts geht. Zu versuchen, diese Phasen für das eigene Spiel zu nutzen, kann nicht verkehrt sein, denn es liegt ja auf der Hand, daß in diesen Phasen besser als durchschnittlich getroffen wurde. Ich weiß um die Einwände (so doof bin ich nun auch wieder nicht), aber statt sich den nächsten "Marsch" mit möglichst komplizierten Satzregeln auszudenken, könnte man sich ja auch einmal darum kümmern. 3. Bei jeder (Verlust)Progression steht man irgendwann vor der Frage, setze ich mehr Stücke auf dieselbe Chancengröße, oder dieselbe Stückzahl auf eine Verbreiterung der Fläche; bei letzterem steigt die Trefferwahrscheinlichkeit zu Lasten der Tilgungsrate. Bei Gewinnprogressionen natürlich umgekehrt. Als Beispiel aus der Praxis: Man spielt nach folgender Satztabelle nacheinander immer bis zum Treffer. Beginn also mit 26 mal eine EZ, wenn noch kein Treffer, dann 13 mal zwei EZ usf. Beim Bestimmen wohin man setzt, hat man völlige Freiheit: man kann raten (was kommt als nächstes?); man kann vorher festgelegte Zahlen spielen; man kann die aus dem Permanenzverlauf nach irgendwelchen Kriterien sich ergebenden Zahlen spielen; man kann sich Scheinspieler einrichten, und versuchen, in deren Ergebnissaldoverlauf "gewinnträchtige" Phasen auszunutzen; alles bisher Genannte durcheinander; etc. Ich habe das letztes Jahr für einige 10.000 Sätze mit schönem Erfolg praktiziert (und dabei, spaltenweise, mit d'Alembert progressiert, es war einfach das Naheliegendste; wenn man noch mehr Zeit investieren möchte, kann man aber auch erst steigern, wenn die Spalte wieder trifft). Zwei Nachteile: unter 1.000, besser 5.000 Stück Kapital fängt man besser gar nicht erst an, und: das Spiel ist unfassbar langweilig. Da muß man dann durch. Ein Dauergewinnspiel ist das aber natürlich auch nicht, das darf man niemals vergessen. Aber für mich gilt in dieser Hinsicht sowieso: fällt die aktuelle Umsatzrendite unter 10%, bin ich sofort raus aus dem Spiel. Gruß elementaar

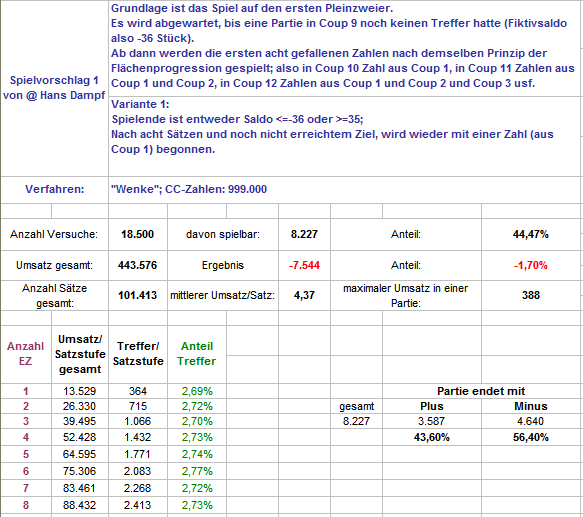
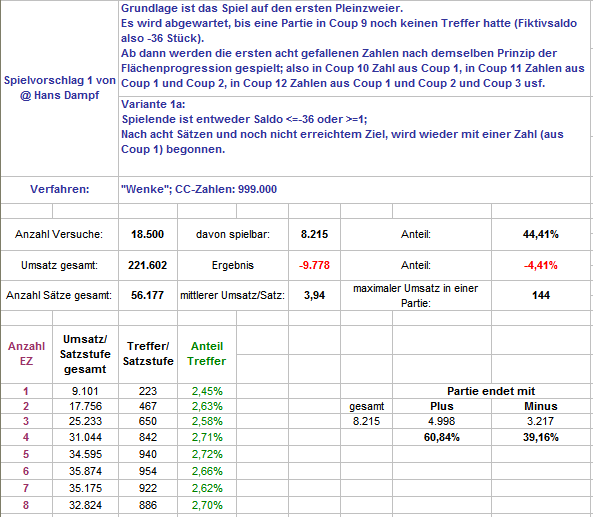
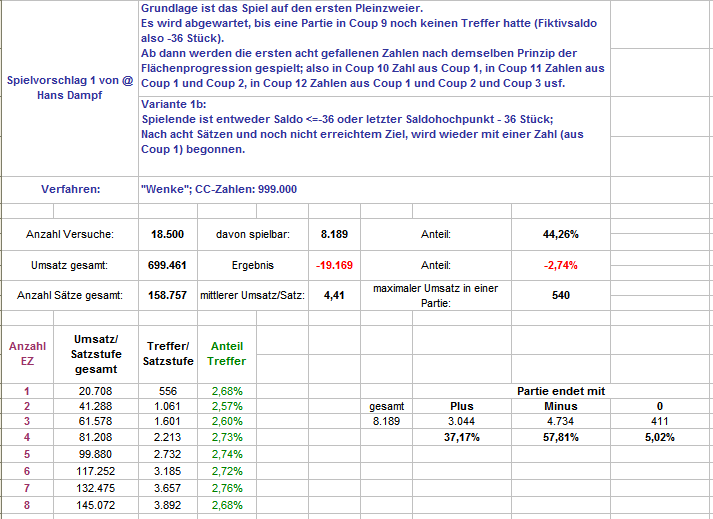
Hallo Hans Dampf, vielen Dank für Deinen Spielvorschlag von hier: https://www.roulette-forum.de/topic/18514-netroulette/page/18/?tab=comments#comment-405418 Ich antworte in diesem Thema, weil es so besser zu passen scheint, obwohl ich ja sämtliche Auszählungen im Gleichsatz mache, die Fläche wurde dabei allerdings progressiert, darum geht es ja. Wie Du schon richtig vermutet hast, sind bei Deinem Vorschlag etliche Varianten denkbar. Zunächst einige, bei denen, falls in den ersten acht Sätzen das Partieziel nicht erreicht wurde, die Flächenprogression wieder mit dem Spielen der ersten Zahl neu aufgesetzt wurde. Es wurden immer 18.500 Versuche ins Spiel zu kommen gemacht. Hier zunächst mit den von Dir vorgeschlagenen Partiezielen (Variante 1): entweder >=35 oder -36 Stück Als nächstes mit einer Begrenzung im Gewinn (Variante 1a): Partieende bei entweder >=1 oder -36 Stück. Wie so oft, wenn man mögliche Gewinne abschneidet, lief dieser Aufbau schlechter als der erste, im Verlauf, mit <-6% vom Umsatz für eine ganze Weile, hätte man besser dagegen gespielt. Als drittes, Variante 1a kann man ja auch anders herum machen, Gewinne laufen lassen (Variante 1b): Partieende bei entweder -36 Stück oder wenn vom letzten Saldohochpunkt 36 Stück wieder verloren wurden. Hier können durchaus Partien mit "0" Stück Endsaldo enden. Zu beachten bitte: die sehr unterschiedlichen Gesamtumsätze. Es wäre natürlich außerdem noch denkbar, daß nach acht Sätzen, statt die Flächenprogression von neuem zu beginnen, einfach mit allen acht Zahlen weiterzuspielen, bis das Partieziel erreicht ist. Weil das aber dem Prinzip der Flächenprogression widerspricht, habe ich dies zunächst nicht behandelt. Gruß elementaar

Hallo Hans Dampf, vielen Dank für das Angebot, und ja gerne, nur heraus damit. Deine immer wieder aufscheinende Fähigkeit, Dir unterhaltsame Falsifizierungsexperimente auszudenken, schätze ich sehr (falls ich das noch nicht explizit geschrieben haben sollte). Schöne Feiertage! Gruß elementaar

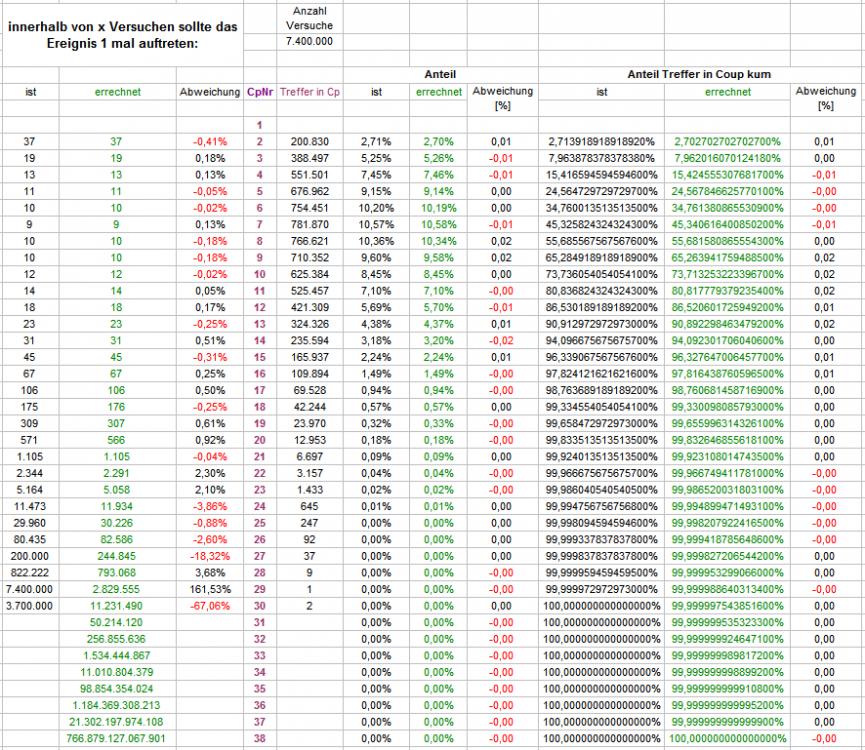
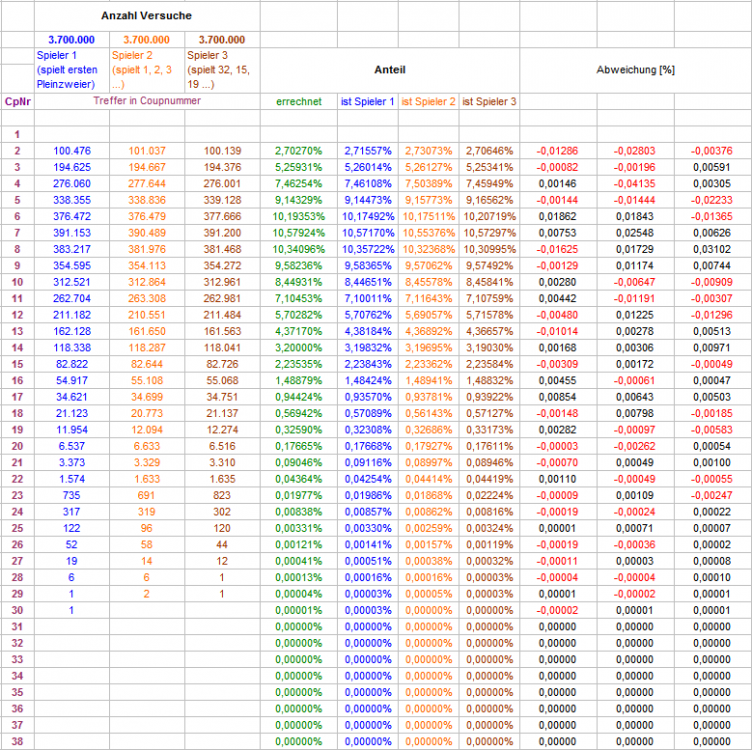
Hallo Hemjo, da kann ich Dich beruhigen: Du bist bloß Zeuge völlig normaler Schwankungen. Bevor Du an Deinen oder meinen Zahlen zweifelst, und voreilige Schlüsse ziehst, könntest Du Dir klar machen, daß es für jedes Ereignis einer genügend großen Menge bedarf, bevor sich die Sollwerte prozentual einpendeln. Und das gilt umso mehr, je seltener ein einzelnes Ereignis überhaupt eintritt. Bei diesem Spiel wird in Coup 2 eine Einzelzahl gesetzt (p=1/37), spielst Du 100 Partien, wäre es schon erstaunlich, wenn Du damit just jene 2,7% aller Treffer verzeichnen könntest, selbst bei 1.000 Partien wäre es noch sehr erstaunlich (es bedeutet ja real, bezogen auf diesen einen Spielzug der Partie: Du hast 1.000 mal auf eine beliebige Einzelzahl gesetzt, erwartest ein 27-maliges Erscheinen, wirst in über 60% der Fälle (mit jeweils 1.000 Partien) mit +- 1 sigma zwischen 22 und 32 Treffern sehen, dürftest Dich aber auch nicht wundern, wenn Du zwischen 12 und 42 Treffern sähest (+- 3 sigma); selbst darüber hinaus Gehendes ist bei dieser Minimenge an Ereignissen nicht etwa Anzeichen für Betrug, sondern eher normales Geschehen. In Coup 19 ( 18 Zahlen zu setzen) hast Du aber eine noch viel kleinere Erscheinenswahrscheinlichkeit als bei 1 EZ (2,7% zu 0,33%). Selbst wenn Du schon 1.000 Ereignisse in Coup 19 hättest (Du hast 1?!), könnte man damit nur halbwegs sinnvoll bis +- 2 sigma rechnen (danach werden die Solltrefferwerte bei -sigma negativ). Je seltener ein Ereignis eintritt, desto heftiger sind die anfänglichen Schwankungen, und desto mehr Ereignisse gleicher Art benötigt man, bis sich der prozentuale Anteil auch wirklich einstellt. Betrachtest Du die ersten drei Spalten der Tabelle (überschrieben mit: "innerhalb von x Versuchen..."), so siehst Du, selbst nach 7.400.000 Partien, in allen Ereigniszeilen Abweichungen bei Soll/Ist im mindestens 1/10-Prozentbereich, nach unten aber deutlich ansteigend. In Coup 19 (mit bis dahin immerhin 23.970 Ereignissen) noch mit 0,61%; der Spielzug mit 18 zu setzenden Zahlen kam also bis dahin immer noch etwas "zu selten" als errechnet. "Dafür" liegt Coup 30 mit bis dahin 2 Exemplaren deutlich "vorn" So ist das halt mit den seltenen und den sehr seltenen Ereignissen: sie können jederzeit auftreten, aber bis sie statistisch etwas aussagen, sind wir alle tot. (Wie gut, daß es hilfsweise Simulationen gibt!) Gruß elementaar

Hallo @Wenke , Es freut mich sehr, daß Du Dich doch noch einmal mit einen Beitrag beteiligst. Dann kann ich Dir wenigstens meinen Respekt und meine Hochachtung für Deine Leistung über die Jahre persönlich zollen. Und eins kann ich mit Überzeugung versprechen: solange ich Auszählungen mit jeweils frischen Zufallsroulettezahlen mache, werde ich das von Dir geschilderte Verfahren anwenden (natürlich mit der in der Wissenschaft üblichen Einschränkung: solange nichts Besseres auftaucht; zur Zeit erscheint mir das allerdings sehr unwahrscheinlich). Allein dafür: ungezählten Dank! Ein echter Problemlöser und eine enorme Arbeitserleichterung. Bei mir schon für viele Jahre in der Praxis angewendet. Zum Thema Forumklima: mir scheint es u. A. ein Problem der "kritischen Masse" zu sein. Das Verhältnis zwischen Leuten, die aktiv etwas tun wollen und den Thekenstehern scheint einfach nicht mehr zu passen. Ich habe hier, im anderen, und englischsprachigen Foren über ein Jahrzehnt mitgelesen. Und immer wieder erlebt, wie potentiell gute Leute, fast als ob ein geheimer Generalplan bestünde, ganz schnell vergrault wurden. Besonders eindrücklich, im anderen Forum, "Michelangelo", der sich nicht zu Schade war, mit einer Engelsgeduld und ausladenden Texten, Anderen selbst die Grundrechenarten zu vermitteln und es durchaus mit der Meute aufnahm. Allein: irgend wann möchte auch ein solcher Mensch mal einen halbwegs adäquaten Gesprächspartner haben. Niemand gibt unendlich lange das Ein-Personen-Wissenssozialamt. Als sich hier, meiner Meinung nach, mit @Alter Schwede etwas Ähnliches anbahnte, dachte ich: jetzt reichts. Jetzt mache ich auch einmal mit. Erfolg: außerordentlich fraglich, nahe der Unmeßbarkeitsgrenze. Vor allem der entschlossene Wille des Partout-nicht-lesen-Wollens ist immer wieder schockierend. Aber: es gibt sie ja hoffentlich auch heute noch: die stillen Mit- und Nurleser. Eigentlich braucht man dafür aber kein Forum, sondern bloß eine Verlautbarungsstelle. Gruß elementaar

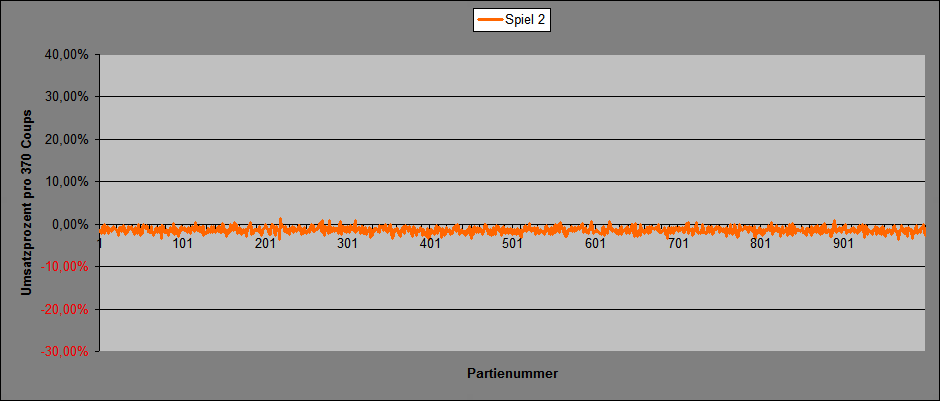
Hallo Hans Dampf, Ja, heftig. Zum Teil natürlich durch den viel geringeren Umsatz auf gleicher Spielstrecke (Spiel 2 war Dein Satz mit 100% Abdeckung: je 8 Stücke Rot und Schwarz, 1 Stück erste Vier (0, 1, 2, 3)) https://www.roulette-forum.de/topic/18514-netroulette/page/12/?tab=comments#comment-404072 Im Vergleich ist auch die Breite der "Rauschmitte" viel unruhiger und dünner. Gruß elementaar

Hallo Egoist, ich danke Dir für das Erläutern meiner Aussagen, und ich stimme Dir zu, was Du schreibst, ist der Inhalt meiner knappen Sätze. Als Erläuterung Deiner Erläuterung: "... daß man mehr Treffer erzielt, als einem zustehen" Das geht natürlich in beide Richtungen: entweder tatsächlich mehr Treffer als die Chancengröße hergibt, oder bei beispielsweise gespielten Zahl-2-2 genügend oft eine oder mehrere Zahlen ausschließen, also praktisch nicht mit aussetzen. Oder eine Mischform aus beidem. Zur Progressionsabteilung des Satzes: "unbegrenzter Kredit" heißt in diesem Zusammenhang Buchkredit. Spielt ein Martingalist lange genug, wird er irgend wann einen Betrag platzieren müssen, der den der geschätzen Anzahl an Atomen im Universum übersteigt. "Praktisch" wird er sich also mit dem Spielveranstalter darauf einigen müssen, daß er die Beträge nur ansagt, statt sie physisch auf den Tisch zu legen. So verhält es sich auch mit der "endlichen" Spielstrecke: er und seine Nachkommen können bis ans Ende aller Zeiten spielen: sie werden immer eine endliche Strecke spielen. Unendlich, als gedachte Rechengröße, gibt es in diesem Universum real ja nicht (Wenn auch der Vorspann einer Fernsehserie da etwas anderes verspricht). Vor längerer Zeit habe ich eine Buchungsmethode geschildert, die die Satzhöhen in Spalten bucht, jede Partie wird zeilenweise nach rechts bis zum Treffer geschrieben. Danach Neuanfang in Zeile 2. Macht man das mit einem Martingalisten, sieht man nicht nur sehr deutlich, wie die Spalten, die Saldoplus verursachen, nach und nach nach rechts wandern (und damit, automatisch, die "mehr Treffer als einem zustehen" in ihrer Spalte produzieren) , sondern auch, daß die immer höher werdenden Sätze nicht nur ihre Zeile (Partie) mit Treffer und Gewinn abschließen. Sie müssen in ihrer Höhe auch den systemisch aufgelaufenen Verlust früherer Spalten ausgleichen. Spalte 1 mit Satzhöhe 1 Stück wird nach der Faustregel für EC nach 50.000 Sätzen selbst mit Glück kein Plus mehr produzieren, sondern auf Dauer -1,35% vom Spaltenumsatz. Je länger gespielt wird, umso mehr frühe Satzhöhenspalten produzieren nur noch Verlust. Und alle müssen durch hohe Sätze einzelner Spalten weiter rechts ausgeglichen werden, damit noch ein Saldoplus erzielt wird. Das Schicksal von @Wenke , wie @ratzfatz es erzählt, muß uns allen Warnung und Mahnung sein, wie gefährlich das wirklich ist. Gruß elementaar

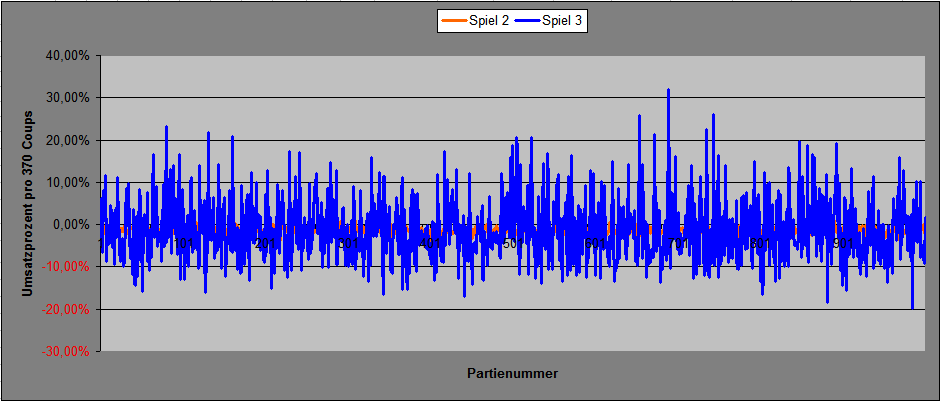
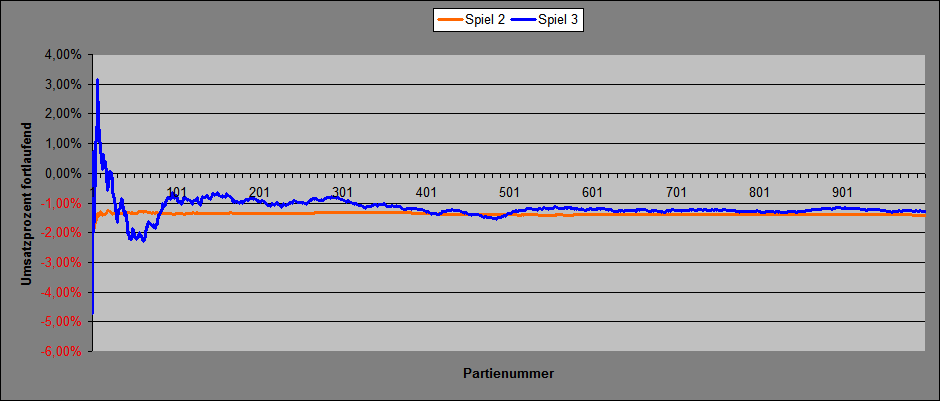
Hallo Hans Dampf (diesmal nur fast 100%), ich habe das neue Satzmuster "Spiel 3" genannt. Einsatz pro Coup 1 Stück die ersten 18 Coups spielt "Rot" mit je 1 Stück die zweiten 18 Coups spielt "Schwarz" mit je 1 Stück Coup 37 spielt "Zéro" mit 1 Stück Einsatz pro vollständiger Sequenz 37 Stück Untersucht wurden Permanenzstücke zu je 370 Coups (Verfahren "Wenke"). Umsatz für die Strecke: Spiel 3: 370 x 1 = 370 Stück Das habe ich 1.000 mal wiederholt. Diagramm 1 zeigt die jeweils nach 370 Coups Spieldauer erzielten Umsatzprozent. Weil die Schwankungen unvergleichlich größer sind, und so Spiel 2 als Vergleich kaum sichtbar ist, hier noch Spiel 2 im gleichen Maßstab wie oben. Diagramm 3 zeigt die Umsatzprozent bei jeweiliger Fortschreibung und Addition der getätigten Umsätze und Saldostände. Bei allem unbedingt beachten: mit Spiel 3 wurden lediglich 370.000 Stück Umsatz gemacht. Ganz andere Hausnummern bei Spiel 1: 52.910.000 Stück Spiel 2: 6.290.000 Stück Umsatz für die Gesamtstrecke: Spiel 3: 370 x 1 x 1.000 = 370.000 Stück Endergebnis für die Gesamtstrecke: Spiel 3: 370 x 1 x 1.000 = -4.770 Stück, entsprechend -1,29% Von 1.000 Spielstrecken à 370 Coups wurden mit Saldo > 0 abgeschlossen: Spiel 3: 352, entsprechend 35,20% Gruß elementaar

Hallo Hans Dampf, danke, und die Ergebnisse vergleichen wir mit Spiel 1 und 2 viel weiter oben. Rot und Schwarz, je 18 x 1 Stück oder 18 x 8 Stück (wie bei Spiel 2), an der Zwischenabrechnungsspielstrecke von 370 Coups möchte ich eher nichts ändern, wären dann hier 10 x 37er Partien, weil ich fürchte, daß sonst die Vergleichbarkeit leidet. Gruß elementaar

Hallo Hans Dampf, ich rätsele, ob ich Deinen Vorschlag gedanklich tatsächlich zur Gänze erfaßt habe. Wir spielen 18 x Rot, egal was passiert? Oder bis zum Treffer (kumulierte Trefferwahrscheinlichkeit bis Coup 18: 0,99999383499002) , egal wie der Saldostand bis dahin ist? Oder bis Saldostand +1 (Erfolgswahrscheinlichkeit ca. 81%)? Danach Schwarz 18 x Dieselben Fragen wie oben (kumulierte Trefferwahrscheinlichkeit bei 18/37 bis Coup 36: 0,9999999961993) Dann Zéro: (1-0,9999999961993) x 1/37 = 0,000000000010272293526; verbleibt (durch die Kettenrechnung) ein Rest an NichtTrefferwahrscheinlichkeit von 0,00000000369802566947. Du siehst an meinem Gestotter, entweder hapert es an meinem Verständnis oder es ist etwas Anderes. Falls Du Dich in der Lage siehst, wäre ich um eine Erläuterung froh. Gruß elementaar

Hallo hemjo, nach allem, was ich weiß, bin ich sofort geneigt, Dir zuzustimmen. Das mache ich aber auch nicht. Und das hat mich auch noch nie interessiert. Bloß weil bei dem, was ich treibe, gezählt wird, und ab und zu auch gerechnet, ist das ja noch keine Mathematik. Am ehesten trifft zu, so würde ich sagen, daß ich es immer noch nicht müde bin zu beobachten, was Zufall so treibt. Gruß elementaar

Hallo Ropro, Es läuft ja in der Tat darauf hinaus, egal ob man in Richtung "mehr Treffer" oder in Richtung "weniger Fehltreffer" blickt. Wobei ich lieber von Treffern und NichtTreffern sprechen würde, um klar zu sagen, daß konkrete Zahlen erst ganz am Schluß wieder eine Rolle spielen, wenn es beim realen Satz darum geht wieviel und wohin. Und diese Verständnisfalle lauert ja überall, ich bin selbst schon zahllose Male darauf hereingefallen, und werde es wahrscheinlich auch in Zukunft nicht vermeiden können. Daß sich mit vdW die Trefferwahrscheinlichkeit nicht ändert ist ja klar. Mein Interesse war zunächst, wieviel (Stück-)Aufwand muß man treiben, bis es zum Treffer kommt (käme eine Progression in Frage und wie müßte sie aussehen?). Sehr schnell stellte sich heraus, daß man sich zunächst um das Problem mit dem "ultimativen Trick" kümmern muß. Dazu habe ich eine Weile mit 4 Farben experimentiert, die ich stufenweise immer asymmetrischer machte. Dabei fiel mir auf, daß in den Simulationen die van-der-Waerden-Zahl (als spätestmöglicher Treffer) bei Weitem und niemals gezählt wurde. Daraufhin, mehr aus Spaß an der Freude, als daß ich wirklich glaubte, damit was reißen zu können, richtete ich 37 Farben (37 EZ) bis Coup 370 ein. Da die van-der-Waerden-Zahl dafür nicht bekannt ist, hat das rein experimentellen Charakter! In 370.000 gespielten Partien kam der späteste Treffer in Coup 264. Niemals mußten alle 37 Zahlen gesetzt werden. Mit der schrittweisen Erhöhung zeitgleicher Scheinspieler konnte ich die Spieldauer, experimentell!, auf unter 40 Coups drücken. Wieder mußten niemals alle 37 Zahlen gesetzt werden. Die Mehrfachtreffer wuchsen jedoch an. Und spätestens da (als geborener Depp wie mir) stellt sich die Frage in Sachen "ultimativer Trick": macht vdW etwas grundsätzlich anderes, als beispielsweise die F4 auf F5. Die Hypothese lautet natürlich "nein", wieso sollte es auch. Es wirklich zu wissen, wird per Experiment auch nicht möglich sein. Aber vielleicht begegnet mir ja noch etwas Anderes, und solange es mir Spaß macht... Gruß elementaar

Hallo ratzfatz, ich danke Dir sehr für diese Informationen. Und was Du schilderst deutet darauf hin, daß er Opfer des Faktors Zeit (trotz Spread 1 : 100.000) geworden ist. Schade! Und den Nachteil haben, außer ihm, wir alle, weil er nichts mehr schreibt. Trotzdem danke! Gruß elementaar

Vielleicht doch noch ein paar erläuternde Worte. @Egoist , @Ropro , @Hans Dampf und auch ich haben ja eigentlich schon genug zusammen getragen, um deutlich zu machen, um was es hier geht. Bei dem Spiel auf den ersten Fx+1 handelt es sich um eine Flächenprogression, und diese ist, wie gezeigt, nicht besser und nicht schlechter als jede andere Flächenprogression, die auf dieselbe Art aufgesetzt wird. Gespielt werden sich vergrößernde Trefferwahrscheinlichkeiten, wie sie jeweils als Zahlen "heißen" ist unerheblich. Der erste Pleinzweier wurde gewählt, weil er in überschaubarster Form am schnellsten zu behandeln ist. Bis Treffer wird in jedem Coup die Fläche (Chancengröße) um eine Zahl vergrößert. Mit dem ultimativen Trick, daß, wenn vorher kein Treffer erzielt wurde, am Ende die Chancengröße 1 (100% aller Möglichkeiten) gesetzt wird, und damit auf jeden Fall der Treffer erzielt wird. Es steckt zwar mehr drin, aber man kann es auch ganz banal ausdrücken: wenn sonst nichts mehr hilft, setzt man einfach alles, dann trifft man auch. Wie man selbst diese Absurdität noch gestalten kann, daß ein Gewinn nicht ausgeschlossen ist, hat @Hans Dampf sehr schön gezeigt. Weiter: Es wird in jedem Coup die zur jeweiligen Chancengröße gehörende Trefferwahrscheinlichkeit gespielt. Wie die Zahlen "heißen", aus denen die Chancengröße besteht, ist ohne Belang. Bei den höheren Fx, also alle F2 zu erstem F3, alle F3 zu F4, usf. wird lediglich das coupweise Anwachsen der gespielten Fläche verzögert. Vor einiger Zeit hat, glaube ich, @Scoville mal ein entsprechendes Experiment angeregt. Man könnte also, beispielsweise, auch festlegen: 8 Coups lang wird eine Zahl gespielt (das kann auch in jedem Coup eine andere Zahl sein), wenn kein Treffer: 8 Coups lang werden zwei Zahlen gespielt (das können auch in jedem Coup zwei andere Zahlen sein), wenn kein Treffer: 8 Coups lang werden drei Zahlen gespielt (das können auch in jedem Coup drei andere Zahlen sein), usf. Man erhöht damit die Dynamik des Spiels und bezahlt mit Zeitaufwand. Mit "Gewinnen" (d.h. nach einer beliebigen gespielten Strecke hat man Saldoplus) hat das alles rein gar nichts zu tun. Dafür ist es nämlich nötig, daß man mehr Treffer erzielt, als einem zustehen (und das gilt ausdrücklich auch für jede Progression: die höheren Einsätze müssen öfter treffen als ihnen jeweils zusteht [und bei unbegrenztem Kredit tun sie das ja, auf endlicher (!) Spielstrecke ]), erstens, um den Auszahlungsnachteil zu egalisieren, und zweitens, um ins Saldoplus zu kommen. Auf dem Weg dahin ist es offensichtlich müßig, d.h. reine Zeit- und Energieverschwendung, in der unmittelbaren Permanenzvergangenheit die Anzahl der gefallenen Zahlen abzuzählen. Dies zeigt unser Experiment sehr eindrücklich. Man kann es natürlich machen (es schadet nicht, und wer wollte es einem verbieten!), aber wozu? Einen Vorteil erlangt man so nicht. Wäre das allgemein klar, wären wir doch schon einmal einen großen Schritt weiter, indem wir wissen, wohin wir nicht mehr schauen müssen! Ich schätze, echte Mathematiker (also solche, die sich mit Mathematik beschäftigen, und nicht bloß rumrechnen, wie es jede Marktfrau (erfolgreicher als manch einer hier!) auch macht), echte Mathematiker also, benötigen unsere Bestätigung gar nicht, ich finde es aber beruhigend, daß auch dieses Experiment bestätigt: das Roulettespiel ist binomialverteilt (Erwartungswert = n x p!). Gruß elementaar

Hallo sachse, wenigstens einen Teil seines Wissens hat er ja dankenswerter Weise in seinen Beiträgen bekannt gegeben. Ich stöbere da immer wieder mal, und sei es nur, um etwas von einem Menschen zu lesen, der offensichtlich seinen Gehirnskasten halbwegs beieinander hatte. Und die Forscher nach dem "Stein der Weisen", neben aller Scharlartanerie, waren die, wahrscheinlich zum Teil unbewußten, Begründer der modernen Chemie. Vielleicht ging es Wenke ähnlich, und er fand etwas ganz Anderes, oder beides. Zu gönnen wär's ihm. Gruß elementaar

Hallo Hans Dampf, danke für die herzstärkenden Worte, vor allem aber: ganz meine Meinung, 100% Zustimmung. Buchstäblich jedes Mal, wenn ich es benutze, geht mein stummer Dank an diese geniale Konstruktion. Und er hat das ja damals eher so unter der Hand geschildert, fast als könnte da jeder darauf gekommen sein, jedenfalls kein großes Gewese gemacht. Außerordentlich und grandios! Da ziehe ich sämtliche Hüte, die ich mir aufsetzen könnte. Gruß elementaar

Hallo Hans Dampf, schön wär's. Aber leider nein; beim Pleinzweier bin ich sowieso nur halb zufällig wieder gelandet, weil sich bei van der Waerden und 37 Farben einiges Interessante ergeben hat, was ich mit dem Spiel Fx -->Fx+1 vergleichen will. Deshalb habe ich den Pleinzweier als einfachster Form wieder hervor gekramt. Mal sehen, wo die Reise hin geht, auf dem Plan habe ich es für die nächste Zeit allerdings nicht. Gruß elementaar

Die Natur der prozentualen Kettenrechnung demonstriert deutlich, daß es rechnerisch ohne Weiteres möglich ist, daß eine gespielte Zahl (auch eine in jedem Coup andere Zahl usf.) beliebig lange nicht erscheint. Der Wert der kumulierten Trefferwahrscheinlichkeit in Coup x nähert sich dabei zwar beliebig nahe an 100% an, kann diese 100% jedoch nur im Unendlichen erreichen (Grenzwert) [1]. Das Spiel auf den ersten Pleinzweier räumt mit dieser Ungewißheit auf: spätestens im 38. Coup ist der Treffer sicher erzielt. Doch womit wird dies erreicht? Aus der Spielidee vollkommen folgelogisch entwickelt, lautet die Anweisung: ist in Coup 37 noch kein Treffer erzielt, werden in Coup 38 alle bis dahin gefallenen Zahlen gesetzt. Dies sind an dieser Stelle 37 Zahlen, und damit alle 37 überhaupt nur zur Verfügung stehenden Möglichkeiten. Das Erreichen von kumuliert 100% Trefferwahrscheinlichkeit wird also erzielt mit einem Satz, der als solcher sowieso schon 100% Treffsicherheit bietet. Bemerkenswerter Trick! Und ein deutlicher Unterschied zum Satz von van der Waerden und den arithmetischen Folgen, wo dieser Trick (mit vielen Farben oder starken Asymmetrien und in der Praxis) nicht angewendet wird. Dieser Trick läßt den Verdacht aufkommen, daß in den vorher gehenden Coups vielleicht auch nicht alles so ist, wie es auf den ersten Blick erscheint. Ist es vielleicht gar nicht entscheidend, wie in den unterschiedlichsten Permanenzentwicklungen die jeweils gespielten Zahlen "heißen"? Folgendes Experiment soll hierüber Klarheit verschaffen: Spieler 1: Er spielt, wie oben beschrieben, auf den ersten Pleinzweier, d.h. bis zum Treffer nimmt er jede gefallene Zahl für den nächsten Coup mit in seinen Satzkorb. Spieler 2: Er kümmert sich nicht um die gefallenen Zahlen, sondern spielt die arithmetische Folge mit der Konstante 1 und der Startzahl 1, d.h. im ersten Satzcoup spielt er "1", im zweiten "1" und "2", im dritten Satzcoup "1" und "2" und "3", usf. Spieler 3: Er macht dasselbe wie Spieler 2, nur nimmt er sich die Zahlen in Kesselreihenfolge, beginnend mit "32" und im Uhrzeigersinn folgend, als Satzanweisung, d.h. im ersten Satzcoup spielt er "32", im zweiten "32" und "15", im dritten Satzcoup "32" und "15" und "19", usf. Damit es auch restlos mit rechten Dingen zu geht, spielen alle drei Spieler exakt die gleichen Permanenzstrecken zeitgleich. Spieler 2 und 3 sind dabei so freundlich und setzen den ersten gefallenen Coup nicht, den Spieler 1 ja braucht, damit er weiß, was er im nächsten Coup zu setzen hat. Wie immer mit dem Verfahren "Wenke", habe ich 3.700.000 Partien spielen lassen, hier die Ergebnisse in Tabellenform: Die Winzigkeit der Abweichungen vom errechneten Sollwert und den drei Spielern untereinander sollten obige Frage beantworten. Gruß elementaar [1] Hierzu noch die Anmerkung: Die irreführende Verwendung der Redeweise "alle x Coup erscheint y", wenn es um die Interpretation des arithmetischen Mittels geht: sie vernebelt, im besten Fall, das tatsächliche Geschehen, und im schlimmsten erzeugt sie Vorstellungen, die das Gegenteil dessen sind, was das arithmetische Mittel ausdrückt. Zur Verdeutlichung stelle man sich die Zahlen in der Reihenfolge des Kessels als Reihe vor: angefangen bei 32 im Uhrzeigersinn bis 26, Zéro lassen wir weg. Je 50% der Zahlen sind, abwechselnd, Rot und Schwarz. Die Redeweise macht daraus: "Alle 2 Coups erscheint Rot." Ein Farben- und eingeschränkt Helligkeitsblinder zählt also ab: 2. Zahl, 4. Zahl, 6. Zahl ... und hat damit eine 50% Chance mit seiner Auswahl von 18 Zahlen kein einziges Mal die gewünschte Farbe zu treffen. Formuliert man hingegen: "Innerhalb von 2 Coup, sollte einmal Rot erscheinen", wird wenigstens die Unbestimmtheit des Erscheinenszeitpunktes angedeutet. Wenn auch hier ein Minderwissender nach dem Erscheinen einer Zahl in Coup 1 glauben könnte, vor dieser hätte er jetzt die nächsten 36 Coups lang Ruhe...