elementaar
Mitglieder-
Gesamte Inhalte
1.437 -
Benutzer seit
-
Letzter Besuch
Inhaltstyp
Profile
Forum
Kalender
Articles
Alle erstellten Inhalte von elementaar
-
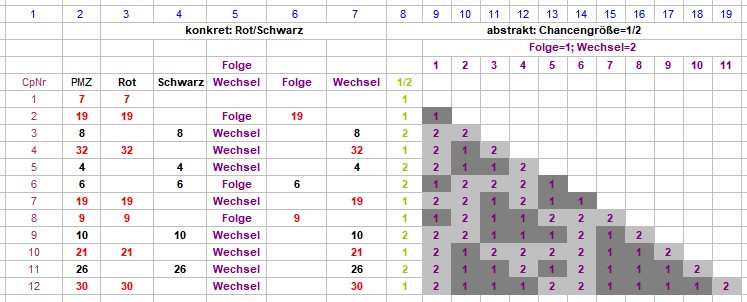
Hallo @Das Kuckuck , damit Euer Gespräch weitergehen kann, und sich nicht in unnötigen Ruppigkeiten über bloße Definitionsfragen erschöpft: möglicherweise um sich einen betont wissenschaftlichen, sozusagen "ernsthaften", Anstrich zu geben, führten die Ludographen der Vergangenheit den Begriff der "Intermittenz" ein. Schaut man sich hier: https://de.pons.com/übersetzung/latein-deutsch/intermittere an, was das Wort bedeuten kann, wird sofort klar, daß es in Bezug auf das Roulettespiel, und speziell in Bezug auf die Einfachen Chancen, alles mögliche, aber nichts Eindeutiges bezeichnet. Sehr viel besser (weil eindeutiger) sind die Begriffe "Folge" und "Wechsel". Sie bezeichnen genau das, was die Worte sagen: "Folge" = die "Farbe" im aktuellen Coup ist dieselbe wie im Vorcoup; "Wechsel" = im Vergleich zum Vorcoup hat die "Farbe" gewechselt. Im Schaubild die Spaltennummern 2 bis 7: dabei in den Spalten 6 und 7 dieselbe Permanenz nach Folge/Wechsel angeordnet. Nach der ersten Folge/Wechsel-Spalte kann man dann natürlich im nächsten Coup auch diese Spalte wieder auf Folge/Wechsel abfragen, und so weitere Spieler erzeugen (Spalten 8 bis 19). Die charakteristischen Dreiecke (in Dunkelgrau) können dabei aus logischen Gründen nur die Folgen bilden. Damit ist das Gegensatzpaar "Folge/Wechsel" eindeutig definiert. @starwind hat nun ein weiteres Gegensatzpaar "Intermittenz/Serie" definiert; entscheidend ist dabei die vergangene Zeit (in Coups gemessen). Dabei ist zu beachten, daß nach jedem Farbwechsel erst der nächste Coup darüber entscheidet, ob eine Intermittenz oder eine Serie vorliegt. Im Schaubild Zeile CpNr 2 "19" ist eindeutig "Serie" auf "Rot", denn Vorcoup "7" war ebenfalls "Rot". Im Schaubild Zeile CpNr 3 "8" ist zu diesem Zeitpunkt nicht eindeutig, erst CpNr 4 "32" bringt die eindeutige Zuordnung "Intermittenz"; wäre CpNr 4 nun ebenfalls "Schwarz" gewesen, würden "8" und CpNr 4 wieder "Serie" gewesen sein. In starwinds Betrachtungsweise wird also gefragt, wieviel (Coup-)Zeit verbrauchen "Einer" ("Intermittenz") und ">Einer" ("Serie"), wobei bei jedem Farbwechsel erst der Folgecoup abgewartet werden muß, um die Erscheinung zuordnen zu können. Nur darauf bezieht sich auch die Tabelle von @Hans Dampf. Gruß elementaar
- 5.148 Antworten
-
- ec
- intermittenz
-
(und %d Weitere)
Getaggt mit:
-
Beobachtung von Wiederholungen
topic antwortete auf elementaar's Bozzi in: Sonstiges zum Thema Roulette oder Artverwandtes
Hallo Bozzi, 31 x NichtRot (Schwarzserie unterbrochen von >= 2 x Zéro). 1990 oder 1991 in Do-Hohensyburg, Tischnummer weiß ich nicht mehr, damals in der Nähe der hinteren Glasfront rechts vom Eingang. Gruß elementaar -
Gibt es Standartwerte für den Rücklauf?
topic antwortete auf elementaar's BerlinerJunge in: Einfache Chancen
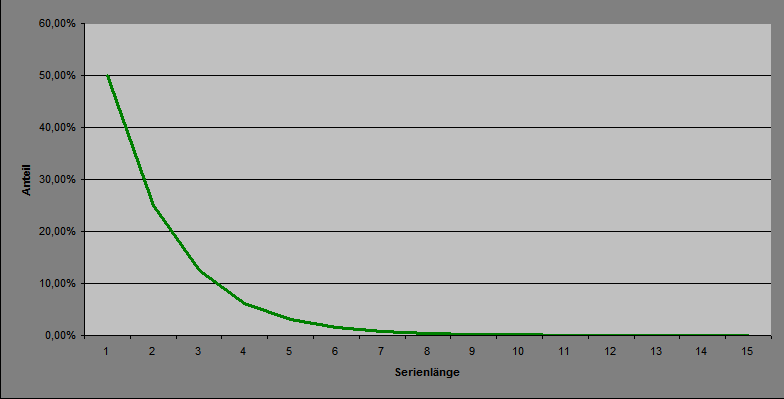
Hallo @Hans Dampf , zunächst die Bitte um Entschuldigung, mir ist oben mit: "Leider nein, die Verteilung der Serien ist linear, stimmt." ein peinlicher Lapsus passiert. Ich habe es oben korrigiert, gemeint war der lineare Skalierungsfaktor, die Kurve ist natürlich exponentiell. So schnell setzt man Falsches in die Welt, es tut mir leid. Jetzt noch die drei Kurven: So, jetzt bin ich aber wirklich zunächst mal weg (ich höre das Aufatmen an der Theke). Gruss elementaar -
Gibt es Standartwerte für den Rücklauf?
topic antwortete auf elementaar's BerlinerJunge in: Einfache Chancen
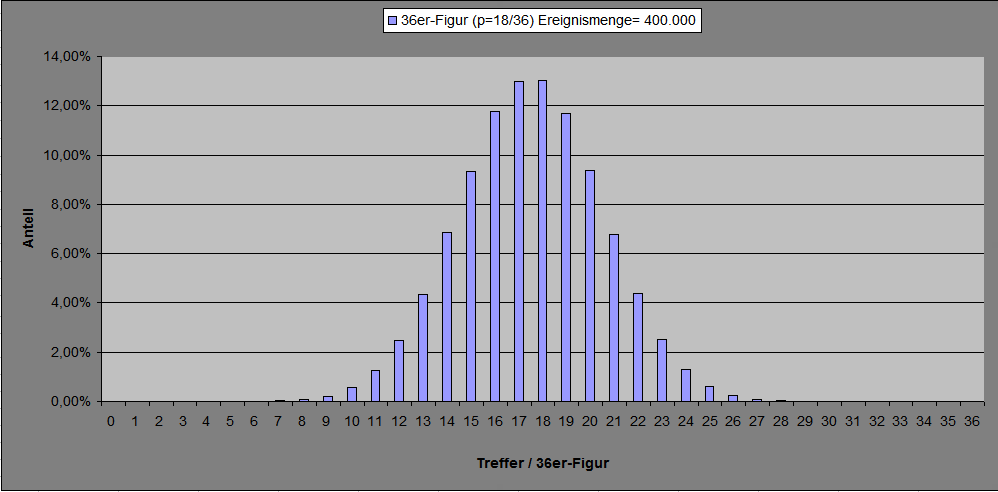
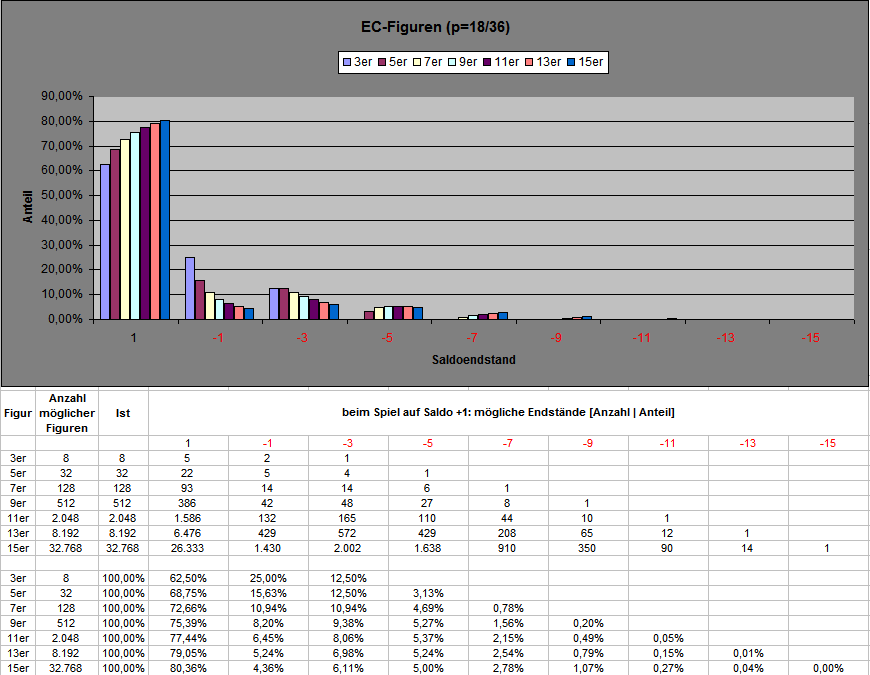
Hallo @Hans Dampf , vielen Dank für die Zusatzinformation. Das ist auch so, zweifellos hast Du da Recht. Das wirkliche Problem liegt aber darin: das ist immer so, vollkommen gleichgültig, was vorher war. Ob irgend ein Spieler vorher +40 oder -40 erzielt hat, oder irgendetwas dazwischen oder auch außerhalb dessen, das ist dem Zufall so was von schnuppe. Wer andere Erkenntnisse hat, möge hier öffentlich den Beweis antreten. Die Verteilung der Serien ist exponentiell, stimmt. Die Verteilung der EC-Figuren (und darum handelt es sich in Deinem Beispiel) ist binomial, und bei einem Spiel auf einen bestimmten Saldostand exponentiell. Vielleicht kann ich später noch Graphen dafür finden und hier einstellen, aber sonst muß ich mich jetzt wirklich verabschieden, ist wirklich keine böse Absicht. Gruss elementaar -
falsche "Berechnung" des Ecart in Fachbüchern
topic antwortete auf elementaar's shogi in: Physikalische Lösungsansätze
Hallo @Das Kuckuck , ausgezeichnete Darstellung! In einem Deiner ersten Beiträge zu diesem Forum hast Du Dich schon einmal so kompetent an einer Schilderung des WW-Spiels versucht, daß es mir positiv auffiel. Da weiß einer, wovon er spricht. Gruss elementaar -
Hallo @kesselman , Dein so überaus freundlicher Beitrag läßt mich erröten... Und gleichzeitig fordert er meinen durchaus freundschaftlichen, aber heftigen Widerspruch heraus. Aus meiner Sicht sind die Worte "Genie" im Verein mit Excel und mir (??!) ganz unangemessen. Und das ist absolut keine Koketterie! Das große Problem ist nämlich mein Gedächtnis: ich weiß immer nur gerade soviel, wie ich für eine anstehende Aufgabe brauche. Danach vergesse ich zuverlässig, was ich einmal spielend beherrschte und muß mir, stellen sich einmal wieder ähnliche Aufgaben, mühsam zusammensuchen, wie damals meine Lösungen aussahen. Manchmal fällt mir darüber etwas besseres ein (Holzhacker eben), ein anderes Mal staune ich selbst, was ich einmal wußte... und darüber verrinnt die Lebenszeit. Wenn ich Dir also, zufällig!, helfen konnte, umso besser, aber weiter keine große Sache. Und vielen herzlichen Dank für Dein erneuertes Gesprächsangebot, die Kontaktdaten habe ich in der Tat noch, wenn es auch im Moment nicht möglich sein wird; dieser beknackte Zwangsumstieg von Win7 zu Linux absorbiert immer noch einen Großteil meiner Zeit, und die Uhr tickt. Viele Grüsse elementaar
-
Hallo @wiensschlechtester , sehr herzlichen Dank, nicht nur für Lob und Preis' , sondern auch für die Schilderung Deines letzten Projekts, und die darin enthaltenen Informationen. Von mir: kappeziehende Gratulation und Verneigung. Herrlich, da sind wir schon zwei - (rheinländisches:) "obwohl" ich bei mir mit den Jahren festgestellt habe, daß die Freude abnimmt - wenn ich nicht aufpasse, bin ich in dreißig Jahren ein ausgemachter Geizhals - möge es die Lebensfreude verhindern. Deinem Beitrag wünsche ich soviele verständige Leser wie möglich, spricht daraus doch sowohl Klugheit wie Praxiserfahrung. Allein bei Deinen Kapitalbetrachtungen sollten den üblichen EC-Adepten die Augen aufgehen. Wenn man schon von den ganz natürlichen Schwankungen nichts wissen will, schaue man sich doch einmal bei den (guten) Pokerspielern um, also denen mit einem echten positiven EW: die rechnen mit mindestens 50-facher bis 300-facher Tischlage als Gesamtkapitalbedarf. Nur, ausgerechnet, bei EC soll es ganz anders sein ("9 Stück + 3-fache Reserve" und dergleichen, erschütternd oder zum Lachen, je nach Temperament). Damit machst Du mich auf etwas aufmerksam, was für Dich ein taktischer Vorteil sein könnte. Ich mache ja dasselbe, nur vom Plein kommend. Dadurch ist für mich die überwiegende Zeit nicht sonderlich erhellend. Umgekehrt, also wie Du es machst, könnte es besser gehen, wie in der Malerei: vom Allgemeinen zum Speziellen... Mit Dank und Gruss elementaar
-
5 ungeklärte Roulettefragen
topic antwortete auf elementaar's Bold Player in: Roulette für Einsteiger / Programmierung / System-Auswertungen / Excel
Hallo @sachse, Aus meiner Sicht ist das ein entscheidender Halbsatz, und gleichzeitig eine zwingende Notwendigkeit: die exakt gleiche Permanenzvergangenheit, muß zwingend zu situativ verschiedenen Satzbefehlen führen. Das ist aber leider noch nicht alles. Denn der scheinbare Widerspruch in obigem Satz läßt sich ohne großen Aufwand (und ohne Bauchgefühl, versteht sich) mit der Satzanweisung: wenn Treffer --> weiter wenn NichtTreffer --> aufhören auflösen. Dadurch wird die eigentliche Fragestellung aber leider nur in den Bereich der Satzhöhen (hier "Moneymanagement" genannt) verlagert. Gruss elementaar -
Gibt es Standartwerte für den Rücklauf?
topic antwortete auf elementaar's BerlinerJunge in: Einfache Chancen
Bei Interesse, Nachtrag und Ergänzung zu oben: https://www.roulette-forum.de/topic/18306-gewinnspiel-auf-einfache-chancen/page/2/?tab=comments#comment-378671 Wie man die EC-Dinge auch betrachten könnte, ist danach recht genau beschrieben, das ist aber dann wirklich etwas ganz Anderes. Und bitte: ich sage nicht, da ist was, sondern, da könnte etwas sein! Aus Zeitmangel kam ich noch nicht dazu, einen mehr als oberflächlichen Blick darauf zu werfen, und eine Übertragung auf andere Chancengrößen ist demzufolge auch noch nicht gelungen. Gruss elementaar -
Gibt es Standartwerte für den Rücklauf?
topic antwortete auf elementaar's BerlinerJunge in: Einfache Chancen
Hallo @Hans Dampf , vielen Dank für Deine freundliche Begrüßung letzthin und Deine Rücksicht. Zu Deiner Frage: es hätten zwar gerne alle, daß es darauf eine eindeutige Antwort gäbe, (das wäre eine mögliche Antwort auf das Gewinnproblem), wirklich "so ist es und basta" und das auch noch in absoluten Zahlen, kann man das bei Zufallsgeschehen nicht beantworten. Also, die richtige und unangreifbare Antwort lautet: Die Frage läßt sich mit p=1 (=sicher) nicht beantworten. Das bedeutet: das weiß kein Mensch und niemand wird es jemals wissen können. Es empfiehlt sich, dies als Faktum zu verinnerlichen. Rechnerisch ist es möglich, daß ein Superpechvogel jeden Tag seines Lebens 100 Sätze auf EC macht, und buchstäblich NIE trifft. Es ist halt eine Frage der Wahrscheinlichkeit, wann dieses Ereignis eintritt; vielleicht ist dieses Universum schon ein einziges Schwarzes Loch und es ist immer noch nicht passiert, es kann aber auch jetzt gleich geschehen. Mit p=1 kann man es nicht wissen. Das gilt übrigens auch für positive EW. Eine Garantie mit p=1 gibt es da auch nicht. Mit negativem EW sieht es aber noch düsterer aus. Das erzielte Sigma muß sich selbst dann exponentiell entwickeln, wenn man lediglich pari aus der Geschichte rausgehen will. Siehe bitte Tabelle hier: https://www.roulette-forum.de/topic/18065-der-satz-von-van-der-waerden/page/9/?tab=comments#comment-361736 Deine von Dir genannten +-40 sind Erfahrungswerte, nach denen oft eine (wenigstens partielle) Trendumkehr zu beobachten ist - ABER: was heißt schon oft? 1. daß es danach steil bergauf oder -ab geht ist eher selten 2. die Seitwärtsbewegung des Saldos nicht vergessen! 3. allenfalls probeweise und mit kleinem Stück anspielen, bei Mißerfolg sofort raus und etwas anderes suchen. 4. auf keinen Fall eine Verlustprogression aufsetzen, das ist eine viel zu gefährliche Situation für solche Späße. Der "Ausgleich" wird sich mit großer Sicherheit anders einstellen als erhofft (siehe 2.) (und @Egoist wird das vielleicht anders sehen). Kommen wir nochmal kurz zu den Sigma-Grenzen. Webpirat hatte im vergangenen Forum für viele Chancengrößen sehr schöne Tabellen erstellt, die finde ich im Moment leider nicht. Für EC mit Zéroteilung und Sigma +3 komme ich, mit eigener Rechnung, als Hochpunkt auf +167 Stück und 11.300 Sätze; mit Sigma +6 kann man länger spielen und hat als Hochpunkt +666 Stück und 50.000 Sätze, Sigma 3 steht dann schon wieder bei Saldo -4. Das sind aber eher Hilfsmittel, um sich verdeutlichen zu können, was gerade passiert ist (Vergangenheit), als daß sich daraus genaue Prognosen ableiten ließen. Eine Garantie, ab hier und da geht es anders herum weiter, gibt es schlichtweg nicht. In der Industrie hat sich eingebürgert, eine Abweichung von 6 Sigmalängen für nicht mehr zufällig zu halten. In der Industrie hat man es aber auch ausgesprochen selten mit reinem Zufall zu tun. Und sie sind außerdem schon mal etwas anderes als die +/- 3 Sigmalängen, von denen der gemeine Spieler, offensichtlich ohne wirkliches Verständnis, brabbelt, obwohl sie zusammengerechnet auch jene 6 Sigma ergeben. Und dann geht es weiter mit diesen 3 von 1000 Fällen, wo +/-3 s überschritten wird, und das ist ja dann "wirklich" selten. Hält man jedoch gezielt nach Abweichungen Ausschau, könnte diese Ansicht aber nicht falscher sein. Man zähle mal Permanenzen bis zum Erscheinen der 37. noch offenen Zahl aus, berechne die Sigma für jede einzelne Chancengröße, und beachte deren Minima und Maxima. Sigma 5,5 oder 5,8 sind keine Seltenheit, und danach ist KEIN spielbares "Aufholen" des Zurückgebliebenen zu beobachten. Mal klappt's, mal nicht - wie immer. Ein Sigma über 6 habe ich so allerdings auch noch nicht gesehen. Im praktischen Spiel nutzbar ist die Sigma-Kurve der eigenen Tr/NichtTreffer z. B. so: standardmäßig satzgenau mitlaufen lassen; wenn man weiter gewinnt UND sich Sigma seitwärts bewegt: Aufhören!, man hat keinen temporär positven EW mehr. Es tut mir leid - schon wieder so viel Text. Hoffentlich findest Du etwas Passendes darin - im Verfassen von Einzeilern habe ich eindeutig Trainingsrückstand. Gruss elementaar PS.: @wiensschlechtester und @kesselman, ich habe fest vor auf Eure Beiträge zu antworten, aber heute geht es nicht mehr, ich kann Euch nur um Geduld und Entschuldigung bitten. -
Hallo @wiensschlechtester , das freut mich aber, wieder mal etwas von Dir zu lesen. Und natürlich völlige Zustimmung zu dem von Dir Geschriebenen. Und doch ist es leider, für mich, nach wie vor rätselhaft, wieso einige klassische Roulettespieler mit ihrem Tun, scheinbar, deutlich besser abschneiden, als jede Simulation, die ich bisher gesehen habe. Stand jetzt, muß ich, wieder leider, davon ausgehen, daß in meiner Werkstatt noch etliche Codezeilen in den Orkus wandern werden, bis, wenn überhaupt, mal ein Lichtlein leuchtet. Manchmal frage ich mich, wieviel Wissen und Verständnis man denn noch anhäufen muß, bis man die evidenten Kniffe in funktionierenden Code verwandelt hat. Vielleicht aus situativem Überdruß, fragte ich mich kürzlich, ob nicht der ganze Ansatz, nämlich der Versuch, menschliches Spielen im Code nachzubilden, nicht doch der falsche sei. Man könnte sich auch fragen: wie würde eine Maschine Roulette spielen... naja, wahrscheinlich Deppengedanken eben. Gruss nach Wien und an Dich elementaar
-
Hallo @Newfish2 , also, jetzt muß ich aber doch sehr bitten! Selbstverständlich haben @kesselman und ich vor dem Zusenden der Datei Vertraulichkeit vereinbart. Und selbstverständlich halte ich mich an diese Vereinbarung. Das wäre ja noch schöner, wenn nicht! Da könnte ich ja gleich mit dem Strick auf den Dachboden steigen. Schon Deine erste Frage hat deshalb die Grenze der Unverschämtheit mühelos überschritten. Und dennoch bekamst Du eine Antwort. Was ich dazu sagen wollte, habe ich oben fast vollständig getan. Wenn Dir nicht gefällt, was Du liest, ist das schade, aber damit wirst Du leben müssen. Dein insistierendes Nachbohren hat etwas Obszön-unmoralisches, wie auch Dein Spekulieren, haltlos Hineininterpretieren und Um- und Verdeuten meines Textes. Laß' gut sein, wir hatten unseren Spaß. Gruss elementaar
-
Hallo @Das Kuckuck , Herrlich! An solchen Satzkonstruktionen habe wiederum ich meine helle Freude. Eigentlich eine Steilvorlage, mir ist nur leider der Esprit etwas abhanden gekommen, da bitte ich um Verzeihung; ich habe wohl doch etwas zu intensiv in den Abgrund geblickt. Ich will mal versuchen, ob ich eine Schubkarre von diesen geheimnisvollen Qunten, Quaten oder Quanten ergattern kann, von denen letzhin die Rede war. Dies wird meiner Verschränkung (hieß es bisher nicht immer Be- ?) sicher abhelfen. Wie das allerdings im Falle jener anderen Quanten (Schuhgröße 47 bitte) funktionieren soll, ist mir rätselhaft, selbst geschenkt. Gruss elementaar
-
Hallo @suchender, stimmt, ja, ist mir auch aufgefallen. Anders als damals hatte ich gestern einen halben Tag Zeit. Und schon opfere ich sie für Newfish2's Begehr ... na ja, so gut ich eben kann ... ich hoffe, er ist zufrieden mit dem Ergebnis ... sonst weiß ich auch nicht mehr weiter ... aber vielleicht zählt ja auch die Geste allein ... die Zeit ist jetzt allerdings schon mal weg. Gruss elementaar
-
Hallo @Newfish2, wenn ich schreibe, daß ich keine Zeit für eine eigentlich interessante Diskussion habe, dann ist damit tatsächlich gemeint, daß ich keine Zeit für eine eigentlich interessante Diskussion habe, aus diesem Grunde schreibe ich die Wörter nämlich auch genau so und in dieser Reihenfolge hin, in der Hoffnung, daß der verständige Leser in der Lage ist, zu erfassen, daß ich keine Zeit für eine eigentlich interessante Diskussion habe. Sollte das bei Dir aus egal welchem Grund nicht angekommen sein, so tut mir das vielleicht leid, ich kann jedoch bezüglich meines Schreibens keine Schuld auf meiner Seite erkennen. Wie ich außerdem, gelegentlich, erwähnte, sind meine Geistesgaben außerordentlich limitiert. Eine überwältigende Menge an Leuten ist unglaublich viel einsichtiger und klüger als ich. Das magst Du nun beklagen, und vielleicht alle anderen mit Dir im Verein, es ändert aber nichts an der Tatsache. Ich - und leider zwangsläufig alle, die mit mir in Berührung kommen - müssen damit leben. Es ist nicht zu ändern. So ist es mir, um ein Beispiel zu geben, nicht möglich, bei Deinen versammelten Einzeilern in so eigenwilliger Grammatik, Rechtschreibung und Gedankenführung intuitiv (und anders scheint es mir auch unmöglich) den Sinn zu erfassen , wie es scheinbar die hier versammelten Permanenzlesergenies durchaus können. Respekt. Ich kann es aber jedenfalls nicht, und raten lehne ich ab, und ob mir das in diesem Fall leid tut, weiß ich nicht und werde auch nicht versuchen, es herauszufinden. Sogar in FETT gedruckt. Echt jetzt?! Was für eine originelle und putzige Idee. Du glaubst also, weil Du gefragt hast (dabei meine damalige Zeitnot ignorierend; manche Menschen, und nicht die schlechtesten, würden das als grob unhöflich auffassen), weil Du also gefragt hast, stünde ich in Deiner Schuld? Da kann ich Dich beruhigen, das ist nicht so. Obwohl Depp, s.o., wie, wann und wem ich antworte, entscheide allein ich (hier bin ich Potentat, hier kann ich's sein), und Dank des in dieser Frage mir innewohnenden Phlegmas, bin ich in der Lage, von mir nicht gegengezeichnete Schuldscheine, egal auch in welcher Höhe und Anzahl, ohne Beeinträchtigung meines Wohlbefindens geflissentlich zu ignorieren. Was könnte damit gemeint sein? (Jetzt rate ich ja doch...Du siehst, ich gebe mir richtig Mühe.) @kesselman hatte also eine Idee (womöglich bezüglich des Roulettespiels)? Die Idee, oder ist es das Spiel, ist aber starr? Da weißt Du mehr als ich, was soll ich da antworten? Oder meinst Du die umfangreiche Datei, die @kesselman mir damals so überaus großzügig hat zukommen lassen? Ja, die ist angekommen. Leider war ich, und bin es immer noch, schon zu doof, um die Plus/Minus-Setzung darin zu begreifen, von weiterem gar nicht zu reden. @kesselman hatte auch sehr schnell ein Einsehen, mit welch indolentem Klotz er es zu tun hatte, und wir beendeten die kurze Korrespondenz durchaus freundschaftlich, auch weil er so höflich meine Dummheit gar nicht zum Thema machte (ich hoffe, dieser, mein Eindruck ist richtig, @kesselman?). Falls also diese Strategie von @kesselman gemeint sein sollte, also dann - nein, die spiele ich nicht, aber nicht etwa, weil sie vielleicht starr wäre (das kann ich gar nicht beurteilen), sondern simpel, weil ich schon in den Anfangsgründen mit meiner Dummheit versumpft bin. Puh - nach dieser langen Epistel ist hoffentlich auch Dir glasklar geworden, daß ich in Deinen Kreisen ein vollkommen ungeeigneter Gesprächspartner wäre, dafür bin ich schlicht zu doof, man könnte geradezu sagen: bei mir hapert's zu sehr in der Birne (oder war's der Apfel?, Würstchen jedenfalls nicht, das war ein anderes Thema, wo der sehr geschätzte @Hans Dampf ...). Wie dem auch sei! Gruss elementaar
-
Hallo @Das Kuckuck, vielen Dank für Dein Lob - es freut mich zu hören, daß Du meinen Beitrag scheinbar lesbar und erhellend fandest. Zumindest glaube ich, daß ich mich bemühe, wenn mir auch bewußt ist, daß meine Mittel als geborener Depp naturgemäß äußerst begrenzt sind, und nur in glücklichen Ausnahmefällen und eher per Zufall etwas sinnvolles dabei herauskommt. Wahrscheinlich kennst Du den alten Witz über drei Fachbereichsvertreter auf dem Weg zu einer Tagung. Ein Soziologe, ein Physiker und ein Mathematiker fahren im Zug zu einer Tagung nach Belgien. Kaum haben sie die Grenze passiert, erblicken sie auf einer Weide zwei schwarze Schafe. Der Soziologe wundert sich: "Kuckt mal, in Belgien sind die Schafe schwarz!" Darauf der Physiker: "Na, na, Herr Kollege, genau genommen können Sie nur sagen: 'In Belgien sind zwei Schafe schwarz' " Lacht der Mathematiker: "Ganz genau genommen können wir lediglich sagen: 'In Belgien sind zwei Schafe auf einer Seite schwarz' " Je nachdem, wer den Witz erzählt, kann man die Rollen von Physiker und Mathematiker austauschen (niemals jedoch die des Soziologen! versteht sich). Danke nochmals für die lobende Rückmeldung. Gruss elementaar
-
Hallo @Egon, danke für Deine freundliche Antwort. Auf den ersten Blick, und im Ergebnis, scheinst Du Recht zu haben, ich muß Dir dennoch widersprechen. Der eigentliche Anlaß meines Beitrags hat sich ja erledigt; nämlich: da verfaßt ein Neuhinzugekommener seinen ersten Beitrag und teilt das (schlüssige, weil mit der Rechnung übereinstimmende) Ergebnis einer umfassenden Auszählung mit. So startet hier nur eine sehr kleine Minderheit - und erntet u.a. Hochmut, ausgerechnet mit der Begründung, daß er das Ergebnis besser hätte ausrechnen sollen. Du argumentierst nun weiter, einfache Wahrscheinlichkeiten müßten nicht überprüft werden - sie lägen sozusagen auf der Hand - und Beispiele mit zusammengesetzten Wahrscheinlichkeiten seien "Obstsortenvergleiche". Es sind genau diese logischen Schnellschüsse und Fehlschlüsse gegen die ich mich mit Vehemenz wehre, weil sie einfach falsch sind und im schlimmsten Fall zu katastrophalen Folgen führen. Zur Erläuterung: 1. Es scheint eine Frage der Logik zu sein, die einfache Wahrscheinlichkeit gleichberechtigter Möglichkeiten als Quotienten aus gewünschtem Ergebnis geteilt durch alle Möglichkeiten darzustellen. Ganz so einfach ist aber auch das schon nicht. Ein Mensch im Mittelalter hätte sofort nachgehakt: "Woher weißt Du denn, daß die angeblich gleichwahrscheinlichen Möglichkeiten auch tatsächlich und in Zeit und Raum gleichwahrscheinlich sind?" Und Recht hätte er, weil er deutlich macht, daß die einfache Rechnung schon auf einer (unbewiesenen) Annahme beruht. Und die Rechenlogik selbst (weil die Gleichwahrscheinlichkeit aller Möglichkeiten axiomatisch vorausgesetzt wird), läuft deshalb auf die Frage hinaus: "gibt es in der realen Welt Situationen, die Gleichwahrscheinlichkeit in genügender Genauigkeit garantieren?" Praktisch also: gibt es bei der zweiseitigen Münze, dem sechsseitigen Würfel, oder den 37 Fächern der Roulette physikalische Fehler, die die Gleichwahrscheinlichkeit verhindern, und wenn ja, in welchem Ausmaß? Ohne ausreichende Prüfung wird man dem niemals auf die Spur kommen, weil die reale Welt nun einmal niemals dem nach ihr modellierten Ideal vollständig entspricht. Absurd genug, daß man immer wieder darauf hinweisen muß. 2. Dieses Forum ist voll von Wortmeldungen, wo wieder mal einer, mehr oder minder aggressiv, und trunken von Begeisterung über seine eingebildete Geisteskraft verkündet: "Dies oder jenes habe ich ausgerechnet, und deshalb ist es wahr." Wieder ein (dem Schreibenden natürlich nicht bewußter, und dennoch) peinlicher Fehlschluß! Vorausgesetzt er hat richtig gerechnet (und das ist in diesem Forum überraschend häufig nicht der Fall), dann stimmt seine Rechnung, ja, aber a) hat er auch die richtige Rechenmethode für die Fragestellung angewendet, und wenn auch hier ja, dann b) entsprechen die zwingend anschließenden, praktischen Versuche auch seiner Rechnung? Denn erst und nur dann ist es in der wirklichen Welt auch "wahr". -- Ich selbst bin KEIN Rechenkünstler, und im Zweifelsfall würde ich mich immer und ausnahmslos auf eine nachprüfbar richtige und fehlerfrei erstellte Auszählung verlassen; mit "Rechnungen" wird in der wirklichen Welt einfach zu viel Schindluder getrieben; mit Statistik allerdings auch, deshalb: nachprüfbar fehlerfrei! -- 3. Meine beiden Beispiele führen die potentiell katastrophalen Folgen vor, wenn in einer Reihe verknüpfter, jeweils einzeln jedoch einfacher Wahrscheinlichkeiten, nur ein einziges Glied falsch gesetzt und gewichtet wird. Irgend jemand sagt zu einem Einzelaspekt, wie Du oben: das ist eine einfache Wahrscheinlichkeit, die muß nicht überprüft werden - und im Ernstfall haben wir den Salat. Die Arbeit von Hunderten von hochqualifizierten Fachkräften über Jahre, der Aufwand von Geldmitteln im Millionen- oder gar Milliarden-Bereich, Menschenleben - alles futsch, wegen eines irren Kindergartenfehlers, der der Division durch Null entspricht: absolut und immer verboten! Die wirkliche Geschichte der O-Ringe enthält übrigens noch eine weitere (auch hier im Forum immer wieder zu beobachtende) Drehung an der Irrsinnsschraube: Das Verhalten des Gummis unter Kälteeinfluß und die daraus resultierenden Undichtigkeiten waren sogar gut bekannt, daraus wurde dann der wahrhaft geisteskranke Schluß gezogen: Weil es bisher immer gut gegangen war, konnten es die O-Ringe gar nicht gewesen sein. Gruss elementaar bei weiterem Interesse bedingt empfehlenswert: Jörg Resag: Feynman und die Physik https://www.springer.com/de/book/9783662547960
-
Hallo @Egon, warum so schnippisch zum ersten Beitrag von @Rabe1? Bringt dieser doch wenigstens Fakten. Oder ist das schon zuviel, nachdem das Forum doch sehr weit überwiegend von zwanghaften Schwätzern gekapert wurde, die wortreich ihre Gehirn- und Wissensverödung dokumentieren müssen. Vielleicht hast Du nur nachlässig formuliert, trotzdem ist diese Aussage schlichtweg falsch. Sobald es um Dinge der realen Welt geht, muß man nach jeder Rechnung (die immer den Modellfall zu Grunde legt) zwingend nachprüfen, ob die reale Welt Befunde liefert, die der Rechnung entsprechen. Dieser Schritt wird von den pseudointellektuellen Rechnerjüngern gerne vergessen und unterschlagen, läßt sich aber absolut nicht umgehen, er ist unerläßlich. Das will aber natürlich heute kaum noch jemand akzeptieren, macht es doch Arbeit und füllt die Spekulation mit Gehalt. Richtig bleibt es aber dennoch, weil es eben keine Meinungsfrage ist, die der Willkür des Einzelnen unterliegt. Beispiele gefällig? Die O-Ringe bei Raketenboostern, deren Zuverlässigkeit bei äußerst dürftiger Datenlage (und damit fahrlässig falsch!) auf 100% gesetzt wurde. Die Folge: die ganze Rechnung stimmt nicht mehr und das Shuttle explodiert beim Start. Die Stelle an Japans Küste, an der das Notstromaggregat für ein Atomkraftwerk zu platzieren sei, wird fahrlässig und geisteskrank falsch gewählt, weil die Wahrscheinlichkeit, daß auf ein schweres Erdbeben ein ebenso schwerer Tsunami folgt, so falsch festgesetzt wird, daß die ganze Rechnung nicht mehr stimmt. Die Folge: Der Notfall tritt ein, das dafür vorgesehene Notstromaggregat fällt durch Überflutung aus, es kommt zum GAU. Wenn wirkliche Welt auf Rechenmodell trifft und dabei Abweichungen auftreten, muß man nachforschen, woran es liegt. Es ist ein sich selbst kontrollierender Regelkreislauf, dem man nicht einfach eine Komponente amputieren kann, ohne schwerste Fehler zu provozieren. Gruss elementaar
-
Betrachtung Roulette/Zufall klassisch
topic antwortete auf elementaar's Verlierer2 in: Tendenzspiel und Persönliche Permanenz
Vielen Dank für die Nachrichten bezüglich K. v. Haller an @Paroli. Und, falls auf diesem Wege erlaubt, alles Gute und herzlichen Dank an Kurt v. Haller. Es muss eine Höllenarbeit gewesen sein, das "Roulett Lexikon" zu verfassen und zusammenzustellen. Und erst das Anfertigen der zahlreichen Grundlagentabellen, mit den damaligen Möglichkeiten... Es wird einem schwindelig, versucht man sich den betriebenen Aufwand vorzustellen. Herausgekommen ist, auch dreißig Jahre nach Erscheinen, das immer noch maßgebliche Standardwerk für diese Art der Roulettebetrachtung. Auch von mir immer wieder mal gerne zu Rate gezogen. Ob sich jemals wieder jemand einer solchen Mühe unterzieht bleibt fraglich, und ist jedenfalls bis heute nicht geschehen. Besten und allerherzlichsten Dank! Gruß elementaar -
Hallo Hans Dampf, leider kann ich aus Zeitgründen bei Eurer interessanten Diskussion nicht mitmachen; deshalb nur kurze Hinweise: https://www.roulette-forum.de/topic/18340-mit-welchen-mitteln-können-extreme-schwankungen-umgangen-werden/page/4/?tab=comments#comment-380617 Dort schrieb ich: Dein Nur-Rot-Spieler mit neun Stück Umsatz könnte seine Schwankungen äußerst wirkungsvoll verkleinern, spielte er statt 3 Cps x 3 Stück mit 9 Cps x 1 Stück. Im ersteren Fall hat er die Chance 1/8 sein Geld komplett zu verlieren, im zweiten sind es lediglich 1/512 (mit 18/36). Je mehr Möglichkeiten eintreffen können, desto geringer (prozentual) die Schwankungen. Falls wir uns darüber einig sind, kann man sich überlegen, wie man den Zeitaufwand, bei gleichem Ergebnis, verringern kann. Das geht, man muß jedoch sicherstellen, daß man die Anzahl der Möglichkeiten gleich groß hält: also entweder je 1 Stück auf Rot an drei Tischen zeitgleich, oder je 1 Stück auf Rot und Impair und Manque an einem Tisch. Immer muß die Möglichkeit vorhanden sein, daß zeitgleich alle Sätze gewinnen können (also nicht ausschließlich das eine ODER das andere). Sonst klappt es nicht. Gruß elementaar
- 5.148 Antworten
-
- ec
- intermittenz
-
(und %d Weitere)
Getaggt mit:
-
Hallo webpirat, vielen Dank für Deinen Zwischenbericht. Und noch besser, daß Du an einer Drittelchancenbetrachtung dran bleibst. Was Du zum "Abschneiden" und dem weiterhin gültigen vdV-Satz schreibst, ist natürlich völlig richtig. Falls Dich die Neugier noch weiter treibt, der (wahrscheinlich überflüssige) Hinweis: Es geht auch, mit jedem gefallenen Coup einen neuen Scheinspieler in einer eigenen Spalte aufzumachen. Dann ist Dein "Abschneiden" automatisch inkludiert, außerdem ergibt das zeilenweise Lesen weitere Kombinationsmöglichkeiten. Gruß elementaar
-
Hallo @webpirat , es freut mich sehr, daß Du van-der-Waerden zum Anlaß nimmst, Dich noch einmal zu Wort zu melden. Laß mich Dir aber zuerst für Deine enormen Verdienste hier und im anderen Forum ein dickes "Danke" sagen. Ganz besonders haben mich immer die Klarheit Deiner Sprache und die Offenheit Deiner Gedanken beeindruckt - und, daß Du Dich auch nicht gescheut hast, zeitaufwändige Kärrnerarbeit zu verrichten und in Tabellenform der Allgemeinheit zur Verfügung zu stellen. Klasse und beispielhaft! Daß leider so wemige sich Dich zum Vorbild nehmen, ist dann eine andere Diskussion. Aber zum Thema: Die Frage läßt sich klar mit "Ja" beantworten. Ein vollständiges Satz- und Ergebnisprotokoll mit 1 Dutzend zu 2+3 Dutzend kannst Du hier: https://www.roulette-forum.de/topic/18065-der-satz-von-van-der-waerden/page/8/?tab=comments#comment-360247 als .pdf erhalten. Mir diente die Datei als Abschätzungshilfe bei der Frage, was denn passiert, wenn man die Chancengrößen asymetrisch macht, bis zu welcher Asymetrie dies noch sinnvoll ist, ob es einen "Umkehrpunkt" des Sinnvollen gibt u.ä. Als nächstes habe ich mir nämlich drei Glieder und vier Farben mit der vdW-Zahl 76 (als spätestmöglichem Treffer) vorgenommen, und da ist ein Aufschreiben sämtlicher Möglichkeiten (4^76 > 10^46 Figuren) zwar machbar aber sinnlos. Ich begann mit 2er-EC-Figuren (ohne Zéro: 10-8-8-10 Einzelzahlen), gruppierte mit Zéro zu 10-9-9-9 Einzelzahlen und verglich mit 13-11-8-5 und 18-6-6-7 Einzelzahlen. Für mich das damals interessanteste Ergebnis war, daß auf jeweils 100.000 simulierte Partien kein einziges Mal die vdW-Zahl 76 auch nur entfernt gespielt werden mußte. Die spätesten Treffer wurden in Cp 31 (für 10-9-9-9), 30 (für 13-11-8-5) und 24 (für (18-6-6-7) erzielt. Darauf folgend ging ich zu drei Gliedern und 37 Farben über. Wenn gewünscht, kann ich versuchen, die Ergebnisse hier ausführlicher darzustellen (das dauert dann allerdings eine Weile). Die vielleicht wichtigste Erkenntnis aus den Versuchsreihen kann man so resümieren: mit allerlei Scheinspielertricks läßt sich zwar die Spielzeit (in Coups) bis zum Treffer eklatant verkürzen, nicht jedoch der durchschnittliche, wie auch der maximale Umsatz pro Treffer. Zunächst würde es mich wundern, wenn sich Deine 6-Strang-Idee anders verhielte. Sie hat allerdings den Charme, daß man die Stränge auch waagerecht lesen kann, und so weitere Kombinationsmöglichkeiten erhält. Ich würde da als erstes prüfen, ob es möglich ist, bei gleicher Ursprungspermanenz unterschiedliche, aber jeweils eindeutige Satzbefehle zu erhalten. Das wäre, meiner Meinung nach, ein Indiz, daß da etwas gehen könnte. Gruß elementaar
-
Hallo Albatros, Prima! Und vielen Dank für die Rückmeldung. Deine Analoga gefallen mir, sind sie doch nicht nur unterhaltsam und amüsant, sondern erfassen auch den Sachverhalt. Und nur für den Fall (und die räumliche Nähe mit dem "Schafswollpullover" könnte das fälschlich implizieren), von meinen Lippen kommt nichts Despektierliches über bloße Rechner, im Gegenteil, wenn man schon rechnet, muß man jeden Ehrgeiz in das richtige Rechnen stecken. Ich wollte jedenfalls nicht in einem Haus wohnen, dessen Statiker sich verrechnet hat, und keinesfalls an ein Medizingerät angeschlossen sein, dessen Hersteller sich bei der Elektronikschaltung verrechnet hat, oder in einem Flugzeug fliegen, dessen Hersteller ... oje, das ist jetzt aber zu realitätsbezogen. Gruß elementaar
- 158 Antworten
-
- double ball roulette
- dublinet
- (und %d Weitere)
-
Hallo Hans Dampf, also Du bist echt Spitze! Vielen Dank für das Fundstück; nach der Rezeptlektüre habe ich zwar beschlossen, von Zubereitung wie Verzehr abzusehen, aber allein der Anblick ... Kaum beschreiblich unter den Lachtränen. Merci natürlich auch an @Das Kuckuck und @hemjo. Gruß elementaar
- 158 Antworten
-
- double ball roulette
- dublinet
- (und %d Weitere)
-
Hallo Albatros, Ganz so weit zu gehen ist nun, vielleicht, doch nicht nötig. Dein Beispiel 2 + 3 = 5 heißt schlichtweg "Rechnen", weil es hier darum geht, eine allgemeingültige Rechenvorschrift der Addition ("Mathematik") mit konkreten Werten zu befüllen ("2" und "3") und zu einem korrekten Ergebnis zu kommen. Und in meinen Volksschulzeiten hieß das betreffende Fach auch noch richtigerweise "Rechnen". Genau das wurde gelehrt und mehr oder minder richtig praktiziert. Heute treiben Erstklässler angeblich und großspurig aber falsch betitelt "Mathematik". Aber woher wissen wir denn, daß die Rechenvorschrift bei der Addition so und nicht anders ist? Und woher das Zutrauen, daß, wenn wir der Rechenvorschrift "Addition" folgen, wann immer wir sie korrekt anwenden, dann auch ein korrektes Ergebnis erhalten? Bei "2" und "3" Äpfeln können wir ja noch physisch nachzählen und sehen, ob die Rechnung stimmt, wie sieht dies aber bei Neutrinos aus? Oder bei sehr großen oder sehr kleinen Anzahlen von Irgendwas? Und wie ist es, wenn wir ganze Vorgänge (die Ergebnisse von ausladenden Rechnungen, Prozessabläufe usf.) addieren? Gelten dann dieselben Vorschriften? Gewiß: das auch von Dir hervorgehobene Wort "NICHTS" ist eine (kleine) Übertreibung, in dem Sinne: in der Mathematik wird ab und zu auch gerechnet. Aber bloß zu einem verschwindend geringen Teil. Eine deshalb zunächst flapsig wirkende Antwort auf die Frage, "wann ist es Mathematik", wäre: je abstrakter (und damit allgemeingültiger), umso mehr ist es "Mathematik". Also: 2 Äpfel + 3 Äpfel = 5 Äpfel oder: 2 Würstchen + 3 Würstchen = 5 Würstchen Das ist Rechnen. Nebenbei wird damit auch klar, daß es etwas wie: 2 Äpfel + 3 Würstchen = 5? was denn nun: Äpfel? Würstchen? nicht geben kann. Für einen Mathematiker sieht Dein Beispiel aber richtig so aus: 2x + 3x = 5x Aus praktischen Gründen wird das "x" als Variable oft nicht hingeschrieben, es ist aber immer noch da, und es wird mitgedacht. Die Marktfrau, die gerade 2 Äpfel und dann nochmal 3 Äpfel in eine Tüte zählt, belegt also in diesem Moment die Variable "x" mit der Art "Äpfel". Der Metzger, der gerade 2 Würstchen und dann nochmal 3 Würstchen auf ein Papierchen zählt, belegt in diesem Moment dieselbe Variable "x" mit der Art "Würstchen". Mathematisch "dürfen" sie das, weil sie in voneinander unabhängigen Gewerken unabhängig handeln. Die Additionsvorschrift gilt sowohl für Marktfrauen wie für Metzger. Ein beides-zugleich-Verkäufer darf dies jedoch so nicht machen. Er muß "Äpfel" mit der Variablen "x" und "Würstchen" mit der weiteren Variablen "y" belegen, sonst geht es mit seinem Geschäft sehr bald schief. Die Additionsvorschrift gilt auch für ihn, er muß aber streng beachten, daß er die eine "Art" nur mit derselben "Art" addieren darf. Das mag sich nun, zumal für diesen alltäglichen Vorgang, unglaublich umständlich lesen, ist aber genau das, was mathematisch hier geschieht. Das eigentliche Zusammenzählen ("rechnen"), beim Verkauf ("Geld" = Variable "z") sowohl für Marktfrau wie Metzger essentiell, ist für den Mathematiker eine Marginalie, er interessiert sich für das, was, wie oben beschrieben, abstrakt passiert, und versucht dieses Geschehen per allgemeingültiger Formel zu beschreiben. Im Falle der Addition ist dies schon vor Jahrtausenden allgemeingültig gelungen. Den Mathematiker interessiert das hinfort nicht mehr, diese Fragestellung ist ja erschöpfend und befriedigend gelöst. Rechnen (und damit die gefundenen Vorschriften ("Formeln") anwenden, selbst wenn ihnen das gar nicht bewußt ist!) tun dann andere (die dies, womöglich, viel routinierter und auch besser können). Mathematiker "erfinden" (und beweisen ihre Richtigkeit) Formeln, Rechner setzen bloß konkrete Werte in die Formeln ein und berechnen das Ergebnis. Ich will nicht gerade sagen, letzeres könne auch von einem begabten Schafswollpullover geleistet werden, aber in diese Richtung geht es. Vor einiger Zeit, vielleicht ist es Dir ja vor Augen gekommen, habe ich hier das Modell der Kettenrechnung erklärt, und dabei nicht nur geschildert wie, sondern auch warum man das so und nicht anders macht. Wenn Du so willst, das war "Mathematik", was bei der praktischen Rechnung herauskommt, ist bloß das Ergebnis von "Rechnen", vielleicht wichtig für den Spieler, klar, aber mathematisch von sehr weit untergeordnetem Interesse. Eine mathematisch interessante Aufgabe wäre hingegen, eine allgemeingültige Formel zu entwickeln, mit der sich zu jedem Spielzeitpunkt die kumulierte Wahrscheinlichkeit ohne Kettenrechnung bestimmen ließe. Mathematik ist es dann aber auch, abstrakt nämlich, sehr schnell zu begreifen, daß es eine solche Formel bei von Coup zu Coup anderen Trefferwahrscheinlichkeiten nicht geben kann, man sich also jegliches Nachdenken (bevor man überhaupt rumrechnet!) in dieser Hinsicht sparen kann. Der PC ("Rechner") mit dem ich dies schreibe, "rechnet" fast pausenlos und meist fehlerfrei, und dennoch käme es mir absurd vor, ihn "Mathematiker" zu nennen, dafür fehlt ihm so ungefähr alles, was einen Mathematiker ausmacht - wie u.a. Abstraktionsvermögen und Einsicht. Falls ich den Unterschied nicht verständlich genug beschrieben habe, zögere bitte nicht, nachzufragen. Ich wollte den Text möglichst knapp halten. Gruß elementaar
- 158 Antworten
-
- double ball roulette
- dublinet
- (und %d Weitere)