elementaar

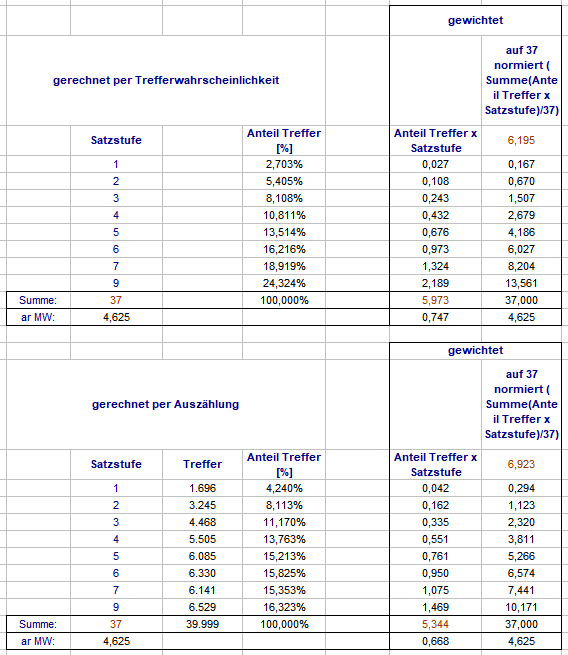
Hallo @Hans Dampf, hilft das vielleicht weiter? Die Trefferwerte (= in der jeweiligen Satzstufe erschienene Zahlen) in der unteren Aufstellung sind durch Addition der letzten Auszählungsergebnisse gewonnen (also NICHT errechnet, sie berücksichtigen NICHT den jeweils erforderlichen Umsatz zum Erzielen der Treffer) Gruß elementaar

Hallo @Hans Dampf, Leider hatte ich gestern Abend keine Zeit mehr, darauf einzugehen. Bei mir kam noch eine lose Assoziationsverbindung hinzu, von einem "Zusammenhang" zu sprechen scheint übertrieben. Wir hatten @Ropros Trick: https://www.roulette-forum.de/profile/40274-ropro/content/page/2/?all_activity=1 https://www.roulette-forum.de/topic/21481-die-hans-dampf-und-charly-setzweise/page/5/?tab=comments#comment-434526 bei dem gesucht wird, in welcher Satzstufe die zuvor gefallene Zahl sich innerhalb der Flächenprogression befindet. Dies wird am häufigsten im 9er-Sektor sein, weil der mit 9/37 die höchste Trefferwahrscheinlichkeit hat. Auch @Ropros Beobachtung der kleinsten Minima schien da auf verquere Art zu passen, denn diese können sich nur bilden, wenn während des Beobachtens genügend getroffen wird (in allen Satzstufen). Ein simples Favoritenspiel (der Satzstufen) wird nicht funktionieren, das wissen wir alle. Beide Ideen, sowohl die von @Ropro als auch die von @Revanchist, haben den Charme, die Treffer der Vergangenheit zwar zu berücksichtigen, aber nicht geradewegs auf sie loszugehen, weil sie versuchen, die Qualität der Treffer mit einzubeziehen. Für mich ließ sich die (reduzierte) Idee von @Revanchist am Ende mit dem kleineren Aufwand realisieren, das gab den Ausschlag, zunächst dies zu versuchen, und das freut mich im Nachhinein besonders, stellte sich doch heraus, daß @Revanchist ebenfalls dran war. Gruß elementaar

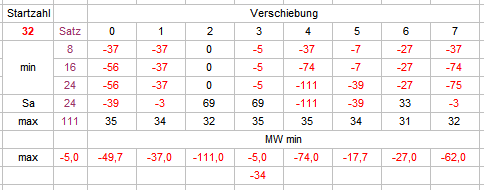
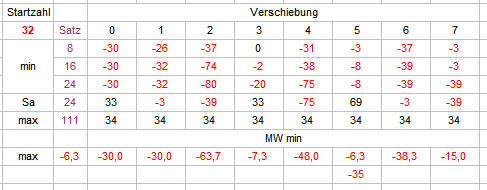
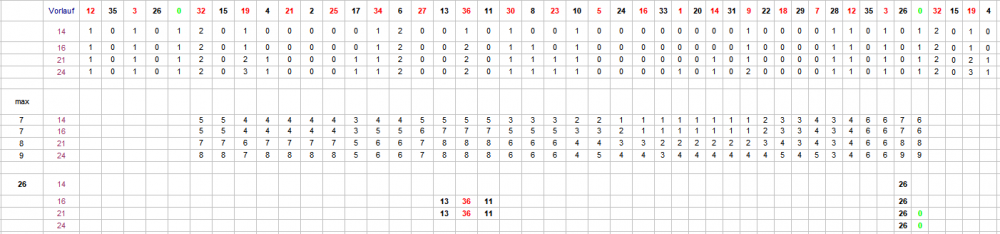
Hallo @Ropro, Je nach dem wie es gemeint ist, stimme ich Dir da sofort zu. Über die Auswertungen zum Vorschlag von @Revanchist schrieb ich: "Nach alter Handwerkertradition (erst mal machen, dann nachdenken) habe ich den folgenden Versuch gemacht." Das sollte als Hinweis doch eigentlich ausreichen, das Ganze nicht zu Ernst zu nehmen. Deinen Hinweis mit den kleinsten Minima bei gewinnenden Startpunkten: Ließe sich das bestätigen, wäre das natürlich eine ganz wunderbare Methode. Ich schildere Dir mal, was ich gemacht habe (es ist sehr gut möglich, daß ich das ganz falsch verstanden habe). Da, wie Du sagst, das Verfahren für jede Startzahl gilt, ist diese also nicht entscheidend. Ich nahm "32", richtete 8 Spieler ein und ließ jeden von ihnen jeweils einen Coup später beginnen. Jeder der Spieler mußte zeitgleich insgesamt 24 Sätze Vorlauf absolvieren. Das führt dann aber leider dazu, daß Spieler 8 seine vollständigen Vorlaufdaten erst liefert, wenn Spieler 1 schon weitere 7 Coups gespielt hat. Also anders: Spieler 8 gibt die gespielte Zeit vor, bei allen anderen Spielern werden 24 Sätze rückwärts gewertet. Der Gesamtvorlauf ist also 31 Coups. Jetzt haben wir zeitsynchrone Daten und suchen den Spieler, der bisher über drei Punkte das kleinste Minus gemacht hat. Spielen alle Spieler in ihrem jeweiligen Satzstufenrhythmus weiter, erhält man nach ganz wenigen (<10) Permanenzerneuerungen z. B. dieses Bild: In den drei Zeilen unter den Bezeichnungsspalten sind die Minima für 8, 16, 24 Sätze verzeichnet; Sa (24) bezeichnet den jeweiligen aktuellen Saldo nach 24 (Vorlauf-)sätzen, also den relativen Startsaldo für unser Spiel; max (111) verzeichnet den Saldohöchstwert von Satz 25 bis Coup 111 (jeder Spieler hat also 80 Sätze Zeit, uns den erhofften Gewinn zu verschaffen). Zum Aussuchen des richtigen Spielers habe ich den arithmetischen Mittelwert gebildet, ergibt dieser "0" sollte dieser Spieler nicht berücksichtigt werden (in wiederum ganz wenigen Versuchen offenbar), deshalb dort die vorsorgliche "-111" Das Beispielergebnis ist nun nicht gerade ermutigend. Weitere Versuche per Hand (<50) waren so katastrophal, daß man fast hätte dagegen spielen können. Also war das wahrscheinlich falsch, was ich da gemacht habe. Neue Tabelle, alles wie zuvor, doch jetzt beginnen alle 8 Spieler nach ihren 24 Sätzen Vorlauf wieder mit Satzstufe 1 Wieder Versuche per Hand (ca. 70). Das geht zwar deutlich besser, aber auch so: Partien mit +50 sind leider die seltene Ausnahme, die Plusergebnisse bewegen sich überwiegend zwischen 2 und paar 30 Stück (und werden ja nur erzielt, wenn man zum jeweiligen Maximum aufgehört hätte, das man da aber noch gar nicht kennt.) Die Ergebnisse differieren so kolossal mit Deinen, daß es ja nahe liegt, einen Verständnisfehler anzunehmen. Ich bitte Dich also um weitere Aufklärung. Gruß elementaar

Hallo @Revanchist, eine Kleinigkeit noch: unter "Anzahl" 2. Zelle müßte als Ergebnis "2" stehen. Ich erwähne es nur, weil das Bildschirmphoto ein Excelblatt zu zeigen scheint. Was Du schilderst, kenne ich nur zu gut - und auf manche derartiger Erlebnisse hätte ich gerne verzichtet. Aber noch viel ärgerlicher wird es, wenn die Kiste ein paar Stunden rechnet und man dann erst auf "ungewöhnliche" Ergebnisse stößt. Lebenszeit ist zu kostbar für eine solche Verschwendung. Gruß elementaar

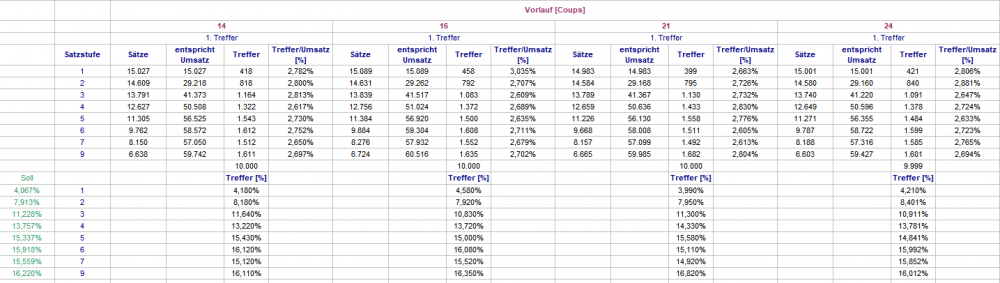
Hallo @Hans Dampf, das kommt ja eher selten vor, daß Du nicht mehr durchblickst. Vielleicht kann ich behilflich sein. Deine Flächenprogression beginnt mit der Startzahl 32 und umrundet dann in insgesamt 8 Sätzen einmal den Kessel. Nun kann man dieselbe Flächenprogression ja auch mit irgendeiner der anderen 36 Roulettezahlen als Startzahl beginnen. Man hat also 37 mögliche Startzahlen mit den dazugehörigen 37 Flächenprogressionen. Welche also nehmen? Aktuell prüfen wir einen Vorschlag von @Revanchist, der auf einfache Weise versucht das herauszufinden und dabei teilweise Ergebnisse von @Ropro integriert. Es werden die ersten 16 gefallenen Zahlen einer Permanenz als Vorlauf betrachtet. Hier werden in einer Art Strichliste die gefallenen Zahlen in Hinblick auf einen 9er-Sektor (als 8. Satzstufe Deiner Flächenprogression) markiert. Der 9er-Sektor mit den meisten Treffern macht das Rennen. Eins daneben im Kessel ist die gefundene Startzahl, mit der dann in Coup 17 sofort das Spiel beginnt. In meinen Tabellen findest Du außer dem 16-Coups-Vorlauf noch den mit 14, 21 und 24 Coups. Gruß elementaar

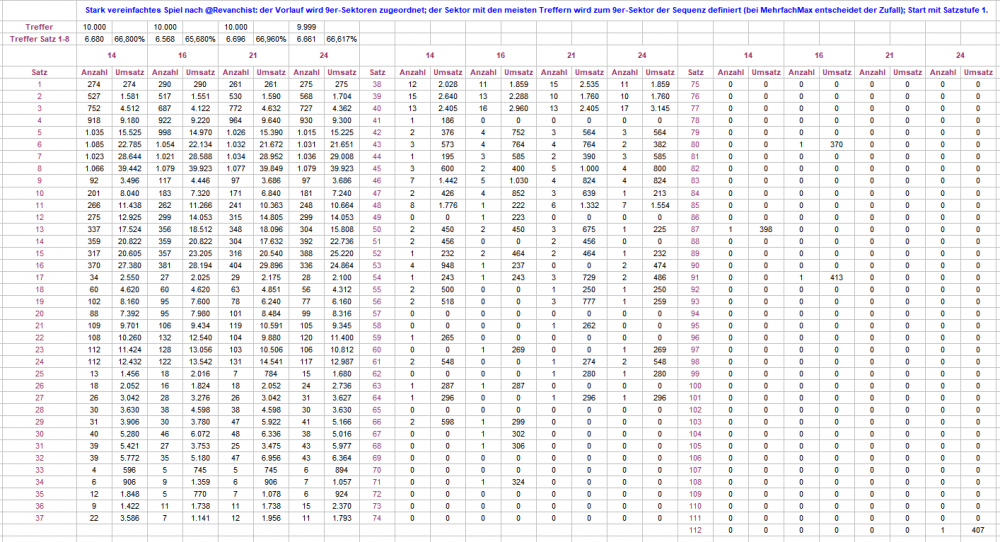
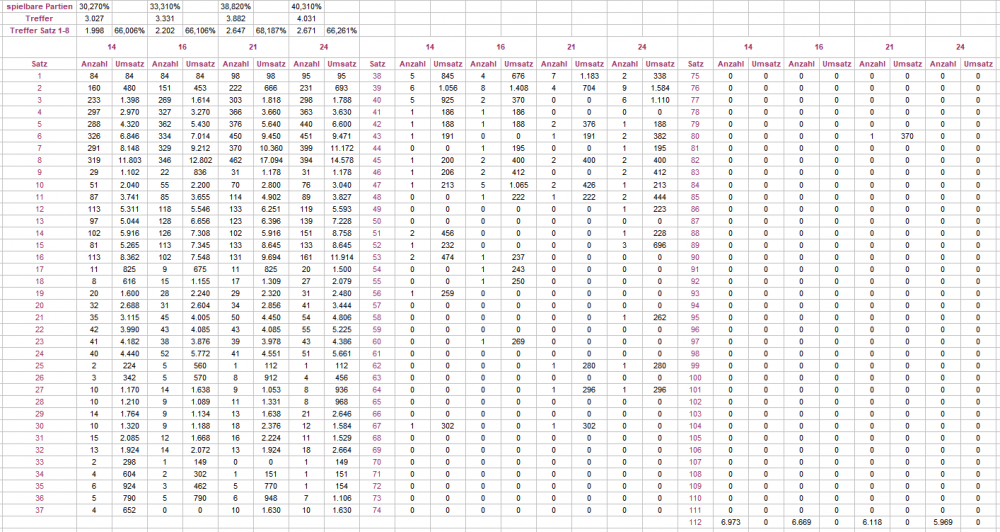
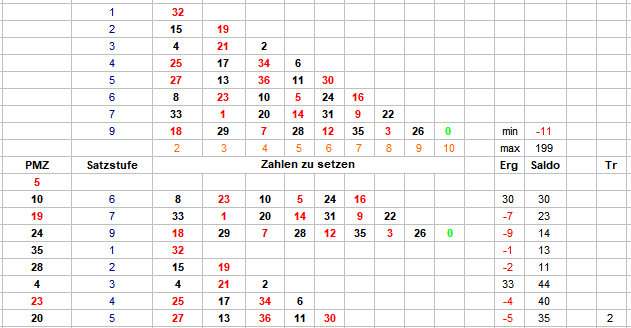
Hier ist eine neue Stichprobe des stark vereinfachten Spiels nach @Revanchist. Im Unterschied zu oben bin ich nun so vorgegangen, daß bei gleicher maximaler Häufigkeit mehrerer 9er-Sektoren der Excel-Zufallsgenerator entschieden hat, welcher Sektor für die Sequenz deklariert wird. Es spielt aber nicht wirklich eine Rolle. Wie zu sehen hat Vorlauf 24 tatsächlich mal einen 112er produziert, allerdings, wie am Umsatz erkennbar, nach lediglich 88 Sätzen. Falls @Revanchist mit Landcasinozahlen nicht noch mit grundstürzenden Ergebnissen aufwartet, sind wir, glaube ich, berechtigt zu sagen: es wird mit dieser Art der Vorlaufanalyse nicht früher getroffen. Aus meiner Sicht begeben wir uns mit derlei Auszählungen in die "wenn man immer dasselbe macht"-Falle, ich bin aber durchaus gespannt, was die anderen Beteiligten sagen. Gruß elementaar

Hallo @Revanchist, herzlichen Dank für die rasche Antwort. Nur schade, daß Du jetzt auf Fehlersuche gehen mußt. Aber dieses Liedchen können wir ja alle singen. Gruß elementaar

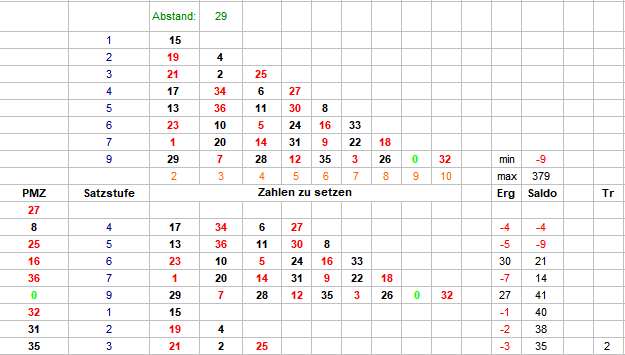
Hallo @Revanchist, drei Fragen hätte ich noch zu Deinem pdf. Ich hoffe es ist erlaubt, daß ich ausschnitthaft ein Bildschirmphoto verwende - ansonsten bitte kurze Meldung, solange möglich werde ich es dann sofort entfernen. Meine Fragen betreffen Coup 15 und 16; gefallene Zahlen "19" dann "32": Gibt es einen Grund, warum "19" aus Coup 15 nur in den oberen vier Sektoren mit 1 verzeichnet ist und nicht zusätzlich in den unteren fünf? Ähnlich "32" aus Coup 16? Bei mir werden da zusätzlich die unteren sieben Sektoren mit "1" markiert. In Zeile 26 bei "Anzahl" sollte da nicht 2 stehen? Bei allen drei Fragen kann es sich um Lappalien handeln, die bloß im pdf so dastehen, nicht jedoch in der Auswertetabelle, dennoch wenn Du Zeit zur Beantwortung finden würdest, wäre das sehr nett. In Sachen mehrfachMAX habe ich jetzt noch ZUFALLSBEREICH eingebaut, der dann den 9er-Sektor bestimmt. Da kann man dann wirklich was wegschaffen. Gruß elementaar

Mal ein wenig spekulieren:

Hallo @Revanchist, vielen Dank für Deinen Bericht. Hoch erfreut lese ich, daß Du Dich derselben Frage angenommen hast. Die etwas andere Programmierung gibt uns damit die immer sehr willkommene Möglichkeit unsere Ergebnisse zu vergleichen. 14:50 Nachdem ich nun das pdf gesehen habe, kann ich Dir nur danken: schon das zweite Mal in kurzer Zeit, von Deiner Finesse profitieren zu können. Heute morgen hatte ich eine kurze Testpermanenz zum Abgleich vorbereitet, das ist jetzt jedoch obsolet. Dein Verfahren ist mindestens insoweit besser, als es den Anteil spielbarer Partien erhöht und damit Zeit spart. Ich werde das zügig einbauen und mich mit neuen Ergebnissen melden, dann können wir vielleicht vergleichen. Gruß elementaar

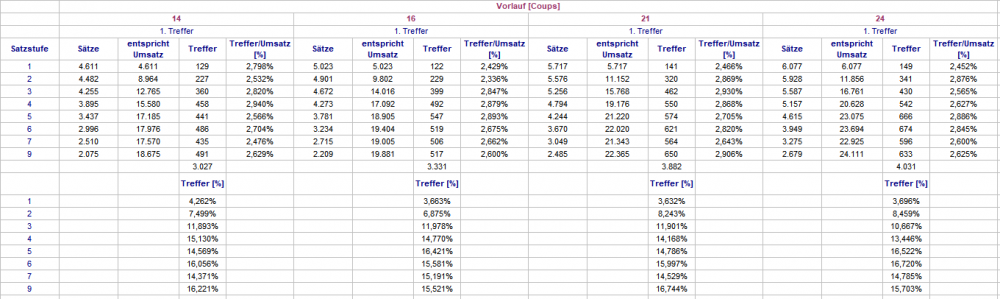
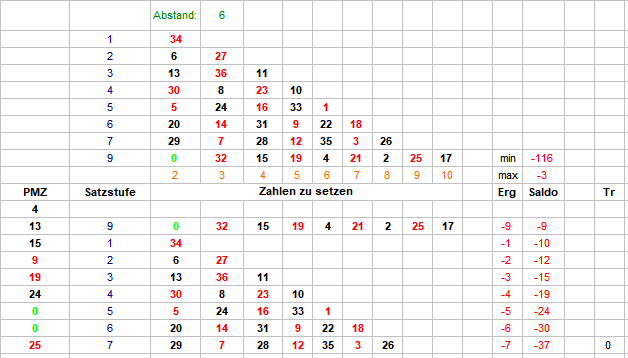
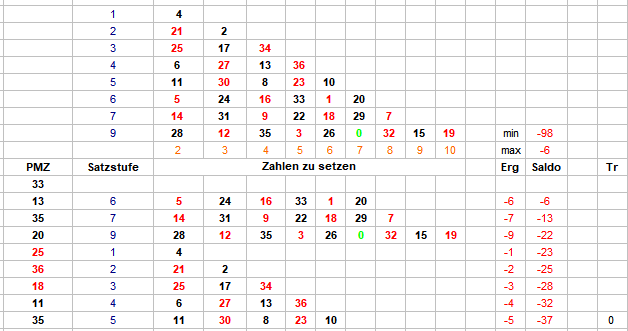
Nach alter Handwerkertradition (erst mal machen, dann nachdenken) habe ich den folgenden Versuch gemacht. Ich habe den Vorschlag von @Revanchist aufgenommen (Du siehst, "mein Interesse zu wecken" ist Dir gelungen. Danke!) und ihn für eine schnelle Auswertung sehr stark vereinfacht. Um bei gegebenem Vorlauf den zu bestimmenden Neun-Zahlen-Sektor herauszufinden, habe ich die gefallenen Zahlen ermittelt, und jeweils über die zwei mal vier Nachbarzahlen die Summe gebildet. Die Zahlen, die mit dem Maximum übereinstimmten, habe ich gekennzeichnet. Dabei kommt dann u.a. so etwas heraus: Ziemlich regelmäßig werden mindestens zwei Kopfzahlen aus unterschiedlichen Kesselsektoren benannt. Da wäre ohne Zusatzarbeit wohl kein Spiel möglich. Ebenfalls sehr oft werden einige im Kessel nebeneinander liegende Zahlen benannt. Im Bild 13, 36, 11 ist einfach: 36 liegt in der Mitte, bei geraden Anzahlen (26, 0) ist das aber dann schon wieder eine Ermessenssache. Dies feststellend, habe ich entschieden, daß für die folgende Auszählung überhaupt nur gespielt wird, wenn eine einzige Zahl als Kopfzahl des Neun-Zahlen-Sektors benannt ist. Über (im Uhrzeigersinn) Abstand 6 wurde sodann die Startzahl (für Satzstufe 1) bestimmt. Es wurde wieder bis zum 1. Treffer gezählt. Dabei zeigte sich bei 10.000 Versuchen, daß lediglich 30-40% der Partien mit dieser Regel spielbar waren. Zeitgleich habe ich die Vorläufe 2 x 7 =14; 2 x 8 = 16; 3 x 7 = 21 und 3 x 8 = 24 auszählen lassen. Hier zunächst die Treffer in den Satzstufen: Sodann die Treffer nach gespielten Sätzen: Die gezählten Umsätze dienen hier nur zur Kontrolle, denn da ja immer bei Satzstufe 1 begonnen wird, lassen sich die zum Trefferzeitpunkt gemachten Umsätze leicht ausrechnen. Satz 112 zählt bei Anzahl die nicht spielbaren Partien, und belegt mit jeweils 0 Umsatzstück, daß auch in dieser Stichprobe kein Treffer über Satz 111 hinaus vorkam. Im Kopf der Tabelle habe ich noch die Treffer bis Satz 8 addiert. Das Soll liegt hier bekanntlich bei 66,46%. Zu einer größeren Stichprobe langte heute die Zeit nicht mehr. Gruß elementaar

[Kurze Zwischenbemerkung ohne jeden fachlichen Mehrwert] Mann Leute, seid ihr schnell! Während ich seit gestern Abend darüber grübele, wie man die Grundidee von @Hans Dampf (auf die gleichzeitige Betrachtung asymmetrischer Sektoren fahre ich voll ab, wie man sich denken kann, mir schwebt da so eine Art "Pendel"-programmierung vor, aber leider noch nichts spruchreifes) mit der Verschiebung kombinieren könnte, kommen darüber weitere bedenkenswerte Beiträge von @Ropro (wie entfesselt!), dann @Revanchist mit ähnlicher Richtung und anderem Ansatz. Wirklich klasse! Das macht zumindest mir großen Spaß (wenn ich auch im Moment Schwierigkeiten mit der Informationsverarbeitung habe) - endlich ist mal wieder fachlich Leben in der Bude. Deshalb meinen herzlichen Dank an alle Mitdiskutanten! Gruß elementaar

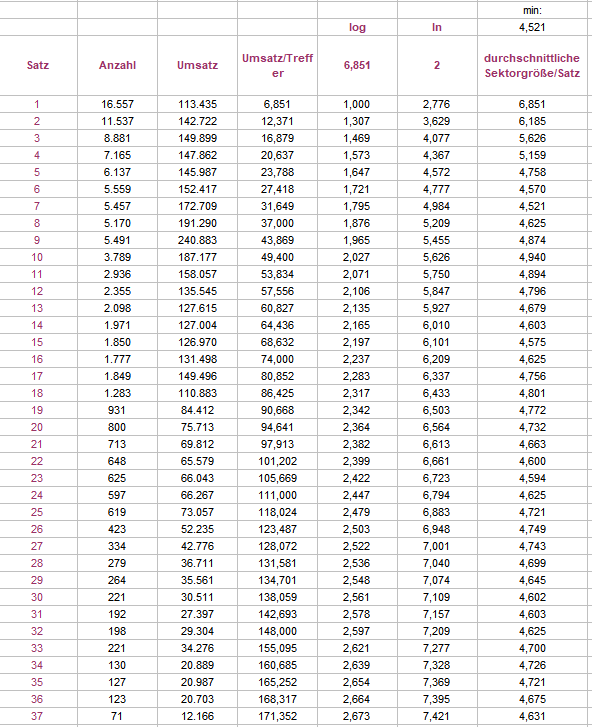
Hallo @Ropro, ich hätte natürlich die Wertetabelle gleich mit einstellen sollen. Teilt man die Werte Umsatz/Treffer durch den jeweiligen Satzcoup in dem der Treffer anfiel, kommt man auf die durchschnittliche Anzahl an Zahlen (=durchschnittliche Sektorgröße), die man bis dahin hätte aufwenden müssen. Der Graph könnte auf ein asymmetrisches Einschwingen deuten. Gruß elementaar

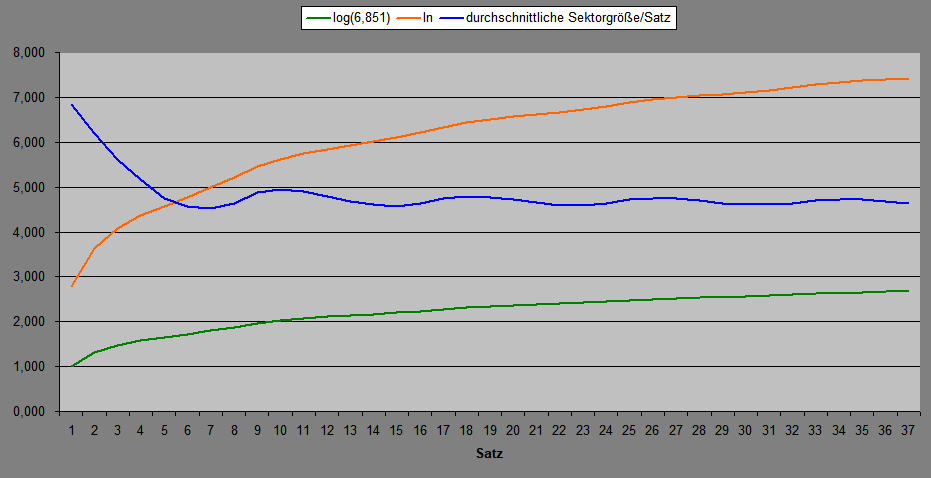
Vielleicht im weiteren Verlauf der Diskussion noch interessant: Das Diagramm zeigt Logarithmen aus der "1. Treffer"-Tabelle weiter oben (Umsatz/Treffer). Einmal den Logarithmus zur Basis 6,851 (=durchschnittliche Sektorgröße bei Treffer im ersten Satz), als zweites den natürlichen Logarithmus (ln). In Blau die durchschnittliche Sektorgröße pro Satz und Zeitpunkt. Die kleinste Sektorgröße wird dabei mit 4,521 in Satz 7 erreicht. Gruß elementaar

Hallo @Hans Dampf, Du raubst mir echt die Illusionen. Nach acht Monaten Totalpause dachte ich so bei mir: "Diese schnelle Flächenprogression ist so simpel, das wird mir den Wiedereinstieg ins Testen erleichtern - ohne daß die mindeste Gefahr besteht, dabei meine Birne unter Anstrengung zu setzen." So anders kann es kommen: das ist ein Blickwinkel, wo mein echtes Interesse geweckt wird. Auch Dir zunächst einmal: Dankeschön! Gruß elementaar

Hallo @Ropro, Da könntest Du einen entscheidenden Punkt geschnappt haben, gratuliere! Sollte sich Deine Beobachtung bestätigen (und aus logischen Gründen spricht, soweit ich sehe, nichts dagegen) wäre auch das Testen ganz wesentlich vereinfacht. Da will ich in den nächsten Tagen mal ein bißchen mit herumexperimentieren. Ob man eventuell positive Ergebnisse am Ende auf einfache Faustregeln reduzieren kann, da bleibe ich skeptisch. Zunächst aber jedenfalls: Danke! Gruß elementaar

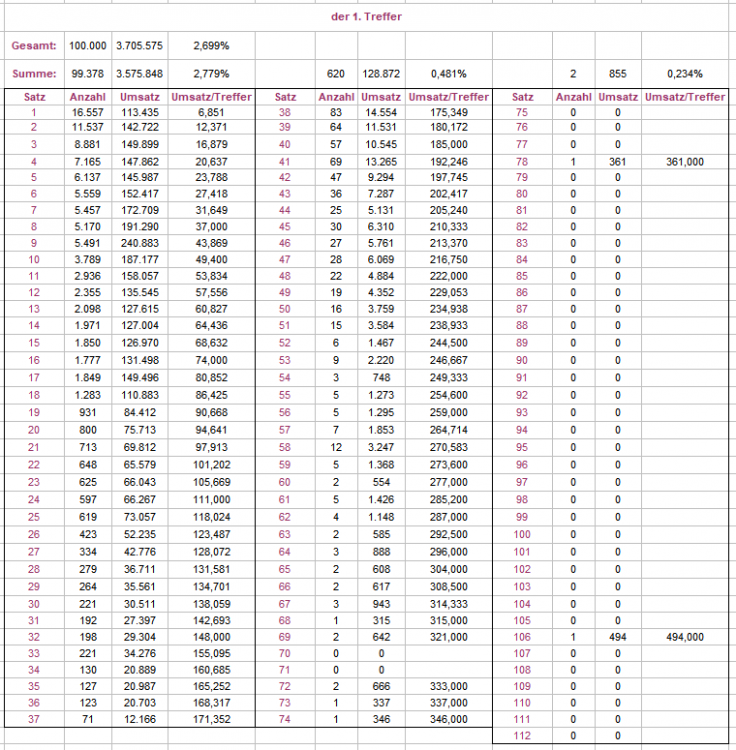
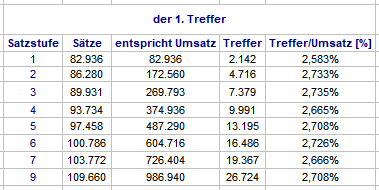
Ich habe noch ein paar weitere Ergebnisse, mit denen ich mich, so fürchte ich, nicht beliebter mache. [Alle Ergebnisse nach Verfahren "Wenke" und der Methode aus meinem zweiten Beitrag "doppelt variabel"!] Zunächst das summarische Ergebnis über 100.000 Versuche, und, was das Erreichen des Partieziels >= +50 Stück angeht, die Beschränkung auf maximal 32 Satzcoups, wie von @Ropro oben angerissen: In dieser Stichprobe liegen die Treffer/Umsatz eine Winzigkeit über dem Soll. Erwartungsgemäß hat sich die Quote erfolgreich beendeter Partien gesenkt, auf runde 37%. Warum nun plötzlich die Vergrößerung der Stichprobe auf 100.000 Versuche? Das hat mit der Frage zu tun, die ich zeitgleich behandelt habe: wann erzielt man den ersten Treffer? Da habe ich nun abgefragt in welchem Satzcoup der 1. Treffer fiel und welchen Umsatz man bis dahin machen mußte. Satz Nummer "112" ist dabei nicht wörtlich zu nehmen; sie ist als Sicherung eingebaut, falls es auf der betrachteten Satzstrecke von maximal 111 Coups nicht zu einem 1. Treffer gekommen wäre; das war nicht der Fall. Ein Fall, wo man auf den ersten Treffer ganze 106 Sätze warten mußte, ist natürlich, wenn man es erlebt, schlimm, der aufgewendete Umsatz von 494 Stück erscheint jedoch für ein Pleinspiel noch erträglich. Zum anderen habe ich gefragt, welche Satzstufe erzielt den ersten Treffer. Lesebeispiel: Satzstufe 3 hat in der Stichprobe 7.379 mal den ersten Treffer erzielt, hätte man in diesen Fällen nur Satzstufe 3 gespielt, hätte man 89.931 mal setzen und damit einen Umsatz von 89.931 x 3 = 269.793 Stück machen müssen. Damit wird die ursprüngliche Flächenprogression nur als Grundgerüst und Datenlieferant verwendet. Ein Spieler könnte beispielsweise beobachten: im Moment läuft Satzstufe 6 über Soll, da probiere ich doch mal mein Glück und spiele nur Satzstufe 6, wenn sie dran ist, bis zum ersten Treffer. Gruß elementaar

Hallo @Ropro, danke für den Dank! Naja, "Mitwirkung" ist relativ, man könnte auch von eher "sachfremdem Einwurf" sprechen. Das Thema basiert auf Zahlen aus Landcasinos, meine Ergebnisse aus "größtmöglichem" Zufall. Ich habe deshalb etwas gezögert die Ergebnisse hier einzustellen. Ich habe es letztlich doch gemacht, weil ich darauf vertraue, daß die, die fachkundig genug sind, den Unterschied erkennen und in der Lage sind, womöglich produktive Schlußfolgerungen zu ziehen, und sei es nur, daß meine Ergebnisse als Vergleichsfolie des "reinen" Zufalls dienen. Was ja zwei verschiedene Grenzen sind, die bloß bei komplettem Nichttreffen übereinstimmen. Die gemachten Tests untersuchen natürlich lediglich zwei Einzelaspekte, nämlich: wird innerhalb einer kompletten Sequenz mit variabler Startsatzstufe "mehr" getroffen? und wie ist die Quote mit erfolgreichen Partien >= +50? Nicht untersucht ist die Frage: wird vielleicht "billiger" getroffen? Was @mona13 gemacht hat, ist mir ähnlich unklar wie @Revanchist. Je nachdem wie die Antwort ausfällt, ist da vielleicht der Verlaufsaspekt schon berücksichtigt. Gruß elementaar

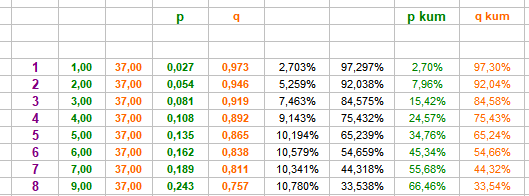
Hallo @Hans Dampf, Ha! Dieser smiley kam mir doch gleich sehr verdächtig vor. Danke für die Mühe. Das hat aber seine Richtigkeit. In dieser Spalte ist für die Kettenrechnung die tatsächliche kumulierte Trefferwahrscheinlichkeit zum jeweiligen Zeitpunkt ausgewiesen, also für sechs Zahlen: 16,2% x 65,239% = 10,579% und dann für sieben Zahlen: 18,9% x 54,659% = 10,341%. Im letzten Satz, wo gleich 2 Zahlen die Fläche vergrößern, steigt der Wert dann wieder an: 24,3% x 44,318% = 10,780% Danke fürs Aufpassen! Gruß elementaar

Hallo @Hans Dampf, eigentlich ist Fehlerkorrektur ja etwas erfreuliches. Als mindestens temporär grobes Holz muß ich Dich aber um nähere Erläuterung bitten, ich kann einfach nicht herausfinden, warum sechs und sieben Zahlen die Plätze tauschen müßten. Habe ich etwas falsch verstanden? Gruß vom Mit-vollem-Gewicht-als-Dauerparker-auf-dem-Schlauch-Steher elementaar

Im oben beschriebenen Versuch wird durch den vorher festgelegten Abstand (19 im Uhrzeigersinn) zur Bezugszahl aus Coup 1 natürlich immer mit dem Satz von sechs Zahlen begonnen. Ich hoffe wirklich sehr, daß es hier niemanden gibt, der glaubt, dadurch würden die Ergebnisse verfälscht. In einer zweiten Stichprobe habe ich dennoch den Abstand per Zufallsbereich(2;37) pro Versuch neu bestimmen lassen (bedeutet im Uhrzeigersinn 1 nach Bezugszahl bis 1 vor Bezugszahl; Satzzahl=Bezugszahl ist wieder ausgeschlossen, weil dies ja die normale Sequenz der Flächenprogression wäre). In der damit "doppelt variabel" festgelegten Satztabelle wird wieder gemäß @Ropros Trick gespielt, also beispielsweise so: oder so: Wieder wurde zeitgleich abgefragt: 1. Wieviele Treffer lassen sich erzielen, wenn einmal alle acht Satzstufen durchgespielt werden. 2. Wie oft wurde das Partieziel mit >=50 Plusstück auf einer Strecke von maximal 111 Satzcoups erreicht. Der Versuch wurde 10.000 mal wiederholt (wie immer mit Verfahren "Wenke"): In dieser Stichprobe liegen die Treffer/Umsatz wieder leicht unter dem Soll (=entspricht den natürlichen Schwankungen). Ich bitte, sich nicht an dem Unterschied erfolgreich erreichter Partieziele zwischen rund 59% in der ersten und rund 60% in der zweiten Stichprobe aufzugeilen. Da hier weder Umsatzdaten noch die Anzahl getätigter Sätze vorliegen, kann diese Differenz sehr wohl innerhalb natürlicher Schwankungen liegen und rechtfertigt keineswegs weitere Arbeiten. Gruß elementaar

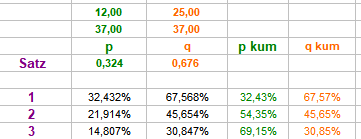
Schauen wir uns doch einmal an, welche kumulierten Trefferwahrscheinlichkeiten eine solch schnell hintereinander gespielte Flächenprogression produziert: Nach dem Einsatz von höchstens 37 Umsatzstück können wir also damit rechnen zu 66,46% getroffen zu haben. Der achte Satz produziert dabei das Ergebnis -1, alle anderen Satzstufen ein mehr oder minder großes Plus. Abgesehen von der Dynamik stellt sich da schon die Frage, warum man so spielen sollte, produziert doch ein simples Dutzend/Kolonnespiel mit weniger ausgesetzten Zahlen (3 x 12 = 36) eine höhere kumulierte Trefferwahrscheinlichkeit, noch dazu mit der Möglichkeit, mit Treffer im dritten Satz, wenigstens mit Saldo "0" aus der Sache herauszukommen. Damit es nicht zu ausladend wird, habe ich diese kleine Auswertung erstellt: Der erste Coup liefert die Bezugszahl. Damit es nun niemals geschehen kann, daß die individuelle "Lieblingszahl" die gerade gefallene ist, wird die gegenüberliegende (im Abstand 19) zur "Lieblings"- (=Start-) zahl deklariert. In der somit festgelegten Satztabelle wird gemäß @Ropros Trick gespielt, also beispielsweise so: oder so: Zeitgleich wurde abgefragt: 1. Wieviele Treffer lassen sich erzielen, wenn einmal alle acht Satzstufen durchgespielt werden. 2. Wie oft wurde das Partieziel mit >=50 Plusstück auf einer Strecke von maximal 111 Satzcoups erreicht. Der Versuch wurde 10.000 mal wiederholt (wie immer mit Verfahren "Wenke"): In dieser Stichprobe liegen die Treffer/Umsatz leicht unter dem Soll (=entspricht den natürlichen Schwankungen). Das erfolgreich erreichte Partieziel pendelt sich schnell auf dann stabile rund 59% ein. Fazit: Wenn man sich nicht die Mühe macht, mit geeigneten Mitteln den Verlauf aufzubereiten, wird man auch mit dieser Methode auf Dauer nicht erfolgreich abschneiden können. Gruß elementaar

Hallo @Hans Dampf, Wobei die Stückwerterhöhung wie die Schwankungsdämpfung über die Zeit wirkt. Per Stückwert wird zusätzliche Zeit gekauft. Vor Jahren gab es einmal einen Spielvorschlag, wo in einem Zehner-Gitter gespielt wurde. Man muß aber nicht unbedingt ein starres Gitter verwenden. Man kann beispielsweise auch irgendwelche 7er-Figuren bis Saldo +1 spielen (die unterschiedlichen Partielängen ergeben dabei ein unregelmäßiges Coupsgitter) und sich für die unvermeidlichen Minus-Partien unterschiedlichen Ausgangs jeweils zeitlich angepaßte Progressions- oder Überlagerungsantworten überlegen. Kombiniert man dies noch mit den unterschiedlichen Erscheinenswahrscheinlichkeiten des Partieausgangs und den daraus folgenden Serien- und Einerbildungen (der Partien), hat man schon mal eine ziemlich gute Beurteilungsgrundlage, was in den nächsten Coups zu tun sei. Das hat durchaus die Chance, lange gut gehen zu können. Gruß elementaar

Hallo @Hans Dampf, Hallo @Egon, so unterschiedlich kann das Wort "schwankungsarm" aufgefaßt werden. Hans Dampf spricht von prozentualer, Egon von absoluter Schwankungsarmut - Dank an Euch beide, diesen Unterschied wieder deutlich dargestellt zu haben. Die absolute Schwankung läßt sich nur verkleinern, indem man den Erwartungswert erhöht. Das muß einem dann aber auch sehr deutlich gelingen; was nützt es einem schon, wenn man auf 1.000 EC-Sätze das erwartbare Minus ab letztem Saldohochpunkt von 95 auf 94 reduzieren kann. Aus meiner Sicht ist das eine unfruchtbare Blickrichtung, selbst als Meßinstrument ("habe ich noch einen pos. EW?") eher ungeeignet, weil viel zu langsam reagierend. Prozentual sieht es dagegen schon anders aus: am EW ändert sich natürlich nichts, die Möglichkeit, durch geschickte Satzweise (und/oder "Zeit") mehr Partien (=wahrscheinlicher eintretend) mit kleineren Schwankungen beenden zu können, das kann für die Spielpraxis schon nützlich sein. Im von Hans Dampf verlinkten Thema muß ich meine Eingangsaussage korrigieren (falls es im darauf Folgenden nicht sowieso geschah): Die darauf folgende, recht ausführliche Untersuchung hat keine belastbaren Belege für einen Unterschied von drei zu einer Signalquelle ergeben. Die festgestellten Unterschiede sind so klein, daß sie 1. innerhalb der natürlichen Schwankungen liegen könnten, und 2. für ein praktisches Spiel ganz sicher keine Relevanz besitzen. Gruß elementaar

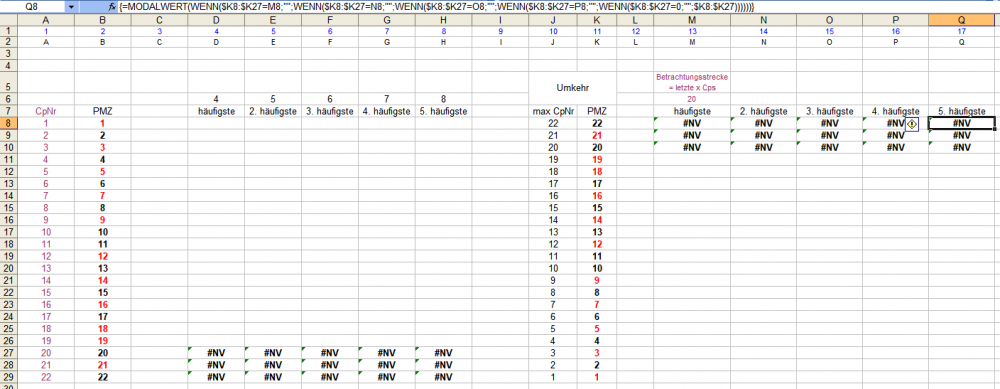
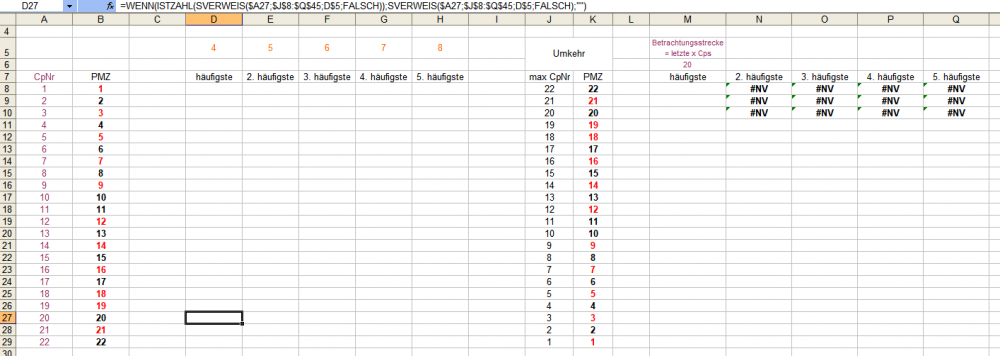
Hallo @Revanchist , vielen herzlichen Dank! Sowohl fürs Bekanntgeben Deiner Lösung, wie die aufgewendete Mühe, sie so übersichtlich wie möglich aufzubereiten, vor allem aber für Deine Findigkeit. Ich ziehe mit Respekt die Kappe! Die Frage per Matrixformel aufzulösen ist wirklich brillant. Sehr gut! Eine Kleinigkeit hätte ich aber noch: Falls es in der betrachteten Coupstrecke keine "häufigste" Zahl gibt (d.h. wenn alle Zahlen nur je einmal erscheinen), oder die x-häufigste nur noch einmal erschienene Zahlen zur Auswahl hat, erhält man die häßliche "#NV"-Meldung, der Ausdruck "WENN($K8:$K27=0;"" " verhindert das leider nicht. Das läßt sich jedoch leicht mit der entsprechenden "ISTZAHL"-Unterscheidung ausblenden. Nochmals danke, und der feine Clou, daß Du Deine Frage am Ende öffentlich selbst beantwortet hast, ist mir nicht entgangen. Gruß elementaar