elementaar
Mitglieder-
Gesamte Inhalte
1.419 -
Benutzer seit
-
Letzter Besuch
Inhaltstyp
Profile
Forum
Kalender
Articles
Alle erstellten Inhalte von elementaar
-
Hallo wiensschlechtester, ein langer und inhaltsreicher Text, und Deine Argumente und Fragen sind gewichtig und deshalb nicht von der Hand zu weisen. Dabei gebe ich zu bedenken: Wie es mir persönlich erging, läßt sich anhand meiner Beiträge zum Thema ja ganz gut nachvollziehen: unabhängig vom Inhalt meiner Schubladen, mußte ich mal wieder extrem reduzierte Geisteskräfte feststellen, die sich, leider, u .a. so äußern, daß man sich kaum mal 15 Minuten am Stück auf ein Thema konzentrieren kann. Buchstäblich und wörtlich. Das Verfassen eines Absatzes eines Beitrags kann sich über eine Stunde ziehen, weil man bspw. mitten im Satz nicht mehr weiß, was man ausdrücken wollte, und worum es überhaupt ging. Das ist beknackt und bescheuert, such Dir irgendein Schmähwort aus - es wird passen. Wäre ich Angestellter im Atomkraftwerk oder Gehirnchirurg, ich müßte mich sofort krank melden. Für mich läuft dann ein persönliches Notstandsprogramm: alles, was man in dieser Situation an nicht erkennbar Sinnlosem behandelt, ist ein kleiner Erfolg. Und dann lese ich die Progressionsidee von Egoist, und zwei Dinge faszinieren mich sofort: 1. das Spielerische, in der Entstehung und in der Ausführung - wirklich charmant. 2. das Fraktalartige. Natürlich nicht auf den Permanenzverlauf bezogen, sondern wie diese starren Satz- und Steigerungsregeln auf Zufallsgeschehen reagieren - elegant, PinkEvilMonkey fand das richtige Wort. Ich hatte sofort das Feigenbaum-Diagramm vor Augen, Bifurkation kam mir in den Sinn. Ob zu recht, wird sich vielleicht noch zeigen. Sich mit derartig reduzierten Geisteskräften ausgerechnet mit etwas zu beschäftigen, wo Fraktale lauern könnten, erscheint Dir als noch gesteigerte Form der Verrücktheit? Da kann ich Dir nicht widersprechen - dessen bewußt, kam es mir als besonders reizvolle und auch geeignete Herausforderung vor. ("Argument": beim Betrachten von Fraktalen muß ich sowieso alle paar Minuten absetzen, weil zu verwirrt. Das paßt ja dann.) Soweit ein Teil der persönlichen Motive, mal abgesehen von dem Vergnügen, überwiegend sachbezogen ein paar Worte mit Egoist wechseln zu können. Nun hat sich mit dem Thema aber etwas entwickelt, was durchaus von allgemeinem Interesse ist, nämlich die immer wieder auftauchende Tatsache der explodierenden Datenmengen bei fortschreitender Betrachtung, und wie man diese bei zu erhaltender Anschaulichkeit behandeln könnte. Egoistens Gedanke, bei im Hintergrund angelegtem 37-er-Zahlensystem, das mögliche Geschehen vollständig in einer 10-Ziffern-Zahl ausdrücken zu wollen, könnte da durchaus zielführend sein. Selbstverständlich kann es sich aber auch als eine Art höherer Kulissenschieberei herausstellen - diese Gefahr besteht aber bei jeder Unternehmung, kein Grund es nicht zu versuchen. Warten wir doch einmal ab, zu welchen Ergebnissen Egoist kommt. Und das Problem exponentiell ansteigender Datenmengen, und wie wir und die von uns erschaffenen Maschinen damit umgehen, begegnet uns ja überall. Da sind 10 Roulettecoups vergleichsweise überschaubar. Gruß elementaar
-
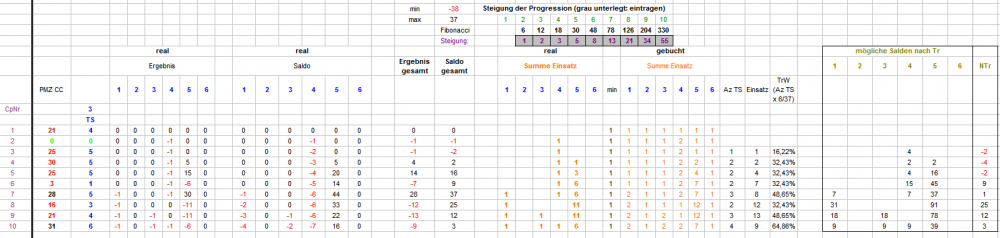
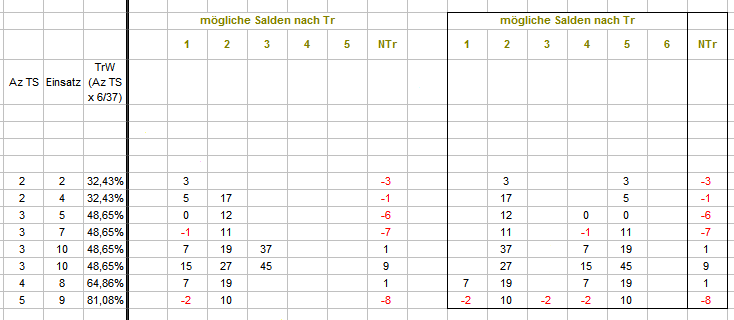
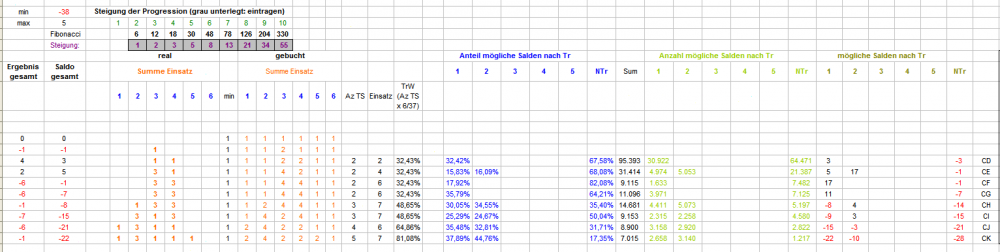
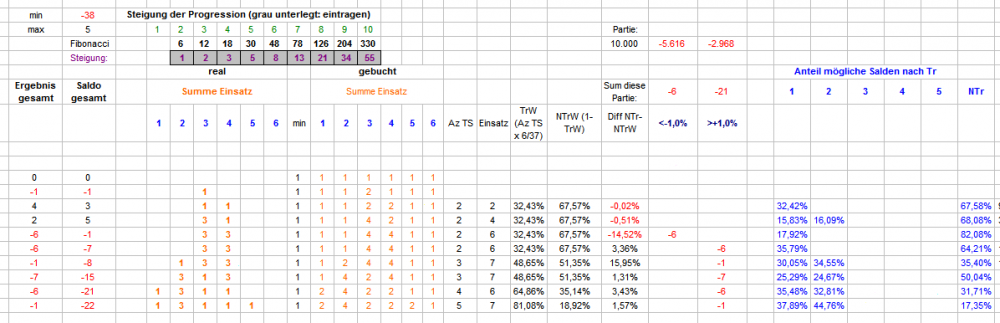
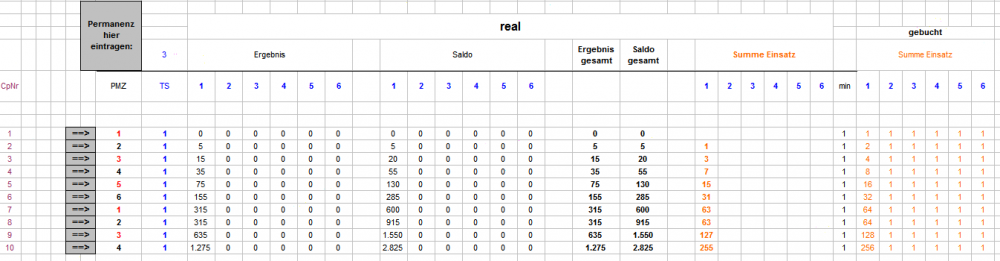
Zunächst die Erläuterung einiger Tabellenerweiterungen: Rechts, unter "AZ TS" wird zeilen- (=coup-) weise summiert, wieviele verschiedene TS zu setzen sind. Eine Spalte weiter, unter "Einsatz" ist summiert, wieviele Stücke zu setzen sind. Aus Anzahl TS x 6/37 ist in der nächsten Spalte unter "TrW" die TrefferWahrscheinlichkeit angegeben. In den nächsten Spalten sind nun die möglichen Salden im nächsten Coup aufgeführt. Dabei interessiert Coup 2 hier nicht weiter (es wird immer ein Stück auf irgendeine TS gesetzt, der Saldostand nach dem Coup ist immer -1 oder +5) Da ein NichtTreffer immer möglich ist, enthält Spalte "NTr" immer eine ununterbrochene Zahlenfolge aus acht Zahlen, die Werte für Saldenstände nach Treffer 1-6 sind dagegen gestreut. Sortiert nach den möglichen, unterschiedlichen Saldenwerten sieht das beispielsweise (mit anderer Permanenz als oben) so aus: Aus den Auszählungsspalten der coupweisen Salden werden jetzt die betreffenden Anzahlen für Coup 3 bis 10 abgefragt und daraus die jeweiligen Anteile in Prozent errechnet. Fragt sich natürlich: was soll der Spaß? Nun, mit diesen simplen Vorarbeiten hat man ein variabel einstellbares Instrument in der Hand, mit dem sich, wenn man will Coup für Coup, feststellen läßt, ob es in der Coupentwicklung Unterschiede gibt. Als einfaches Beispiel habe ich hier zusammengestrickt: Gibt es Unterschiede in der Ergebnisentwicklung, wenn man die Differenz zwischen NichtTreffern der bisherigen Auszählung und der NichttrefferWahrscheinlichkeit bildet? Differenzen von +/- 1,00% sollen uns (wegen der Schwankungen in den realen Anzahlen) nicht stören und werden deshalb vom Satz ausgeschlossen. Die setzbaren Ergebnisse werden in zwei Spalten sortiert und über die gesamte Partie summiert. Für das Beispiel habe ich 10.000 Partien laufen lassen (dabei wurde nach jeder Partie selbstverständlich der Entscheidungsbaum ergänzt, und nein, das ist kein wirkliches "Lernen"). Die beiden Ergebnisse dieses Tuns sind oben in Summe angegeben, und zeigen einen bemerkenswerten (im Verlauf auch stetigen) Unterschied. Gruß elementaar PS.: bis nächste Woche muß ich meine immer noch maladen Restgehirnkräfte anderen Aufgaben zuwenden. Viel Vergnügen beim Weiterpuzzeln!
-
Hallo Egoist, Das fürchte ich allerdings auch. Oh ja, und aus meiner Sicht solltest Du auch unbedingt damit weitermachen, ich schätze den Fortgang Deiner Überlegung sehr. Auch im Sinne eines sauberen wissenschaftlichen Vorgehens ist es ja gar keine Frage, daß Du es richtig machst; und ich mich hingegen auf einer eigentlich unerlaubten (und auch bloß erhofften Abkürzungs-) spur bewege. Meine Hoffnung dabei ist, daß, wenn wir am Ende unsere Ergebnisse vergleichen, sich diese gegenseitig erhellen oder erläutern könnten. Dir auch einen schönen, hoffentlich schmerzfreien, Tag! Gruß elementaar
-
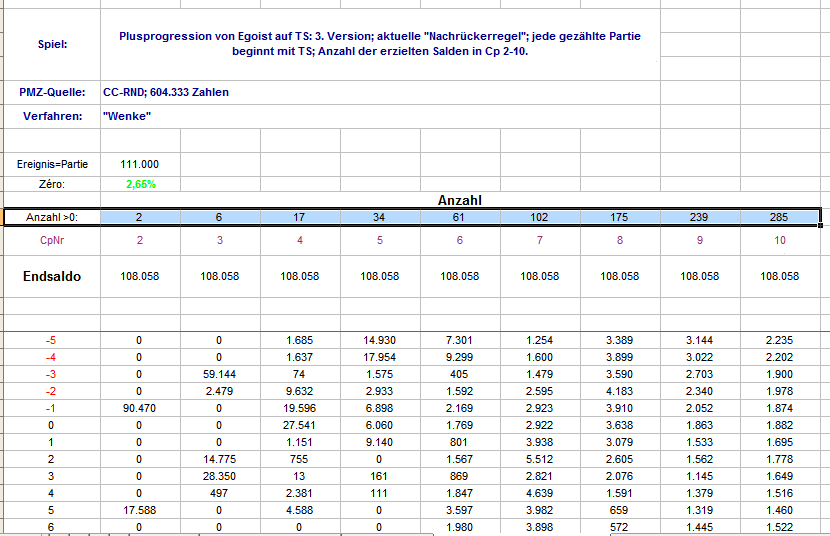
Ungeachtet der mahnenden Worte von @wiensschlechtester an die Spielkinder (und in meinem Fall sind sie gewiß auch oft angebracht), habe ich gestern eine Tabelle angefertigt, in der die Anzahl der Saldenstände von Coup 2 bis Coup 10 verzeichnet sind. Dabei kam dasselbe Verfahren wie oben ausführlich beschrieben zur Anwendung, mit der neuen Regel: jede gezählte Partie muß mit TS in Cp 1 anfangen (ein realer Spieler würde, im Falle von Zéro zu Partieanfang, einfach den nächsten Coup abwarten). Dadurch reduzieren sich die Möglichkeiten des Anfangs des entstehenden Entscheidungsbaums (Pfad) im 2. Coup auf 2: -1 und +5. Ich habe 111.000 Partien zählen lassen, wovon 108.058 in die Auswertung kamen, was einen leicht unterdurchschnittlichen Zéro-Anteil von 2,65% ergibt. In Zeile 26 "Anzahl >0" ist die Anzahl verschiedener Saldozustände verzeichnet, die sich, auf dieser Strecke, real gezeigt haben. TS_PlusProgression_Egoist_06_F.xls Wie es damit weitergeht, hoffe ich heute oder spätestens morgen zeigen zu können. Gruß elementaar
-
Hallo Egoist, Natürlich nicht - und es ist für mich durchaus faszinierend zu lesen, wie Du die Pfade Schritt für Schritt weiter entwickelst. Aber: wenn ich es richtig sehe, verteilst Du Treffer und NichtTreffer im Gleichsatz. Bei Deiner wunderbaren Idee (und das ist für mich ihre reizvollste Eigenschaft) haben wir es aber mit, in der Stückhöhe, gewichteten Treffern/NichtTreffern zu tun, die noch dazu durch Differenzsatz und Nachrückerregel situativ nochmals gewichtet werden. Für mich ist das tatsächlich zunächst eine Frage des Beobachtens und in Folge des (vielleicht und ansatzweise) Begreifens: was passiert da, wenn man die verschiedensten Permanenzen anlegt. Wie wirken sich die verschiedenen Gewichtungsmaßnahmen real aus. Da sind wir im Moment. Als warnendes Beispiel sei da die Suche nach dem größten Minus angeführt: wir alle, die wir uns dazu geäußert haben, lagen zunächst falsch - das Zusammenspiel der verschiedenen Regeln hat schon in dem eng umgrenzten Möglichkeitsraum des negativen Partieausgangs zur Überraschung geführt. In sehr weiter Ferne, also für den Fall, daß wir überwiegend etwas zu Begreifendes begriffen haben und dazu noch für den Unterfall, daß es am Ende etwas gibt, was sich zu validieren lohnt, für diesen noch sehr entfernten Fall sehe ich die angesprochenen Datenmassen. Dies ergibt sich allein aus einer sehr groben Schätzung: Möchte ich wissen, wie sich ein TS-Ereignis verhält, ist das (möglichst) mehrfache Zusammenschreiben von 37.000-Ereignisportionen (Erfahrungswert) nötig Möchte man dies bis einschließlich Coup 10 machen, UND beschränkt sich auf den Bereich von Saldoendstand -38 bis +38 ( und hat damit knapp 94% der Fälle erfaßt), kommt man auf ein Minimum von 77 x 37.000 = 2.849.000 zu simulierenden Partien. Jetzt kann man natürlich den zu untersuchenden Bereich noch wesentlich geschickter auswählen, keine Frage, immer wird es aber Saldoendstandspositionen geben, die noch deutlich mehr Daten erfordern, als im Minimum gerechnet. Nach derzeitigem Stand kosten ca. 600.000 Partien knapp einen Arbeitstag Rechnerzeit... Ich hoffe, es wird verständlich, warum ich mir jetzt schon, obwohl noch sehr fern, Gedanken über die möglicherweise zu leistende Arbeit mache, und versuche abzuschätzen, wohin das alles führen könnte; zumal mit dem möglichen Zusatznutzen des vielleicht besseren Begreifens. Gruß elementaar
-
Hallo Egoist, nur kurz, und nicht zur Sache: Dein Schachbrett-mit-Eierbechern- und-Reis-Bild liest sich köstlich, amüsant und unübertrefflich. Noch größere Anschaulichkeit mit disparaten Elementen dürfte schwerlich zu erreichen sein. Und es ist ja auch noch, soweit ich sehe, wahr. Das macht Spaß. Vielen Dank! Ich möchte hoffen, daß sich auch @coocie dafür begeistern kann. Gruß elementaar Und etwas Erquickung aus der horizontalen Lage!
-
Hallo Egoist, Mann, Egoist, das war aber eine produktive Nacht - und das, wie ich annehmen muß, unter Schmerzeinwirkung. Ich lese, bin entzückt und staune. Und dann noch die Tipperei mit einem Arm... Vielen Dank und Respekt! Und weiterhin beste Genesungswünsche. Du hast Deine Schritte für die "Quantitative Totalanalyse eines Roulettesystems für 10 Ziehungen" auch sehr gut und klar beschrieben. Dabei stellt sich heraus, daß unsere Gedanken in dieselbe Richtung gehen, gestern Nachmittag habe ich ebenfalls mal wieder Überlegungen zu diesem Thema angestellt. Beim pfadweisen Aufschlüsseln kann sich dann auch Dein originelles 37er-Heptatriacontimalsystem bewähren. Den damaligen Zweiflern sollte ein kleines Licht aufgehen. Eine Kleinigkeit zu der angegebenen Anzahl der Möglichkeiten (und natürlich ist wolframalpha sehr empfehlenswert): Bei 7^10 komme ich auf jene 282.475.249 Möglichkeiten; mit der vereinfachten Kurznotation auf 282.475.249 / 7 = 40.353.607 Möglichkeiten, die, wie Du richtig feststellst, durch Zéro p=1/37 und 6 x p=6/37 nicht gleichwahrscheinlich sind. Dabei muß ich gestehen, daß mir das Denken in diesen Pfaddiagrammen immer etwas fremd geblieben ist. Auch für @wiensschlechtester scheint das der natürlichste erste Schritt zu sein, Du machst es ebenfalls - und es hat ja unbestreitbare Vorteile, da will und, mangels Argumenten, kann ich gar nicht diskutieren - und später, wenn valide Daten vorliegen mache ich das natürlich auch. Es könnte eine Frage der Ausbildung, Gewohnheit oder schlicht der persönlichen Vorlieben sein. Zusammengefaßt: eigentlich sehe auch ich nur Vorteile in dieser Vorgehensweise, lese auch die Schilderung mit Freude und dennoch fremdele ich etwas. Seit der Vorstellung Deiner Progressionsidee rätsele ich über zwei Fragen: 1. Wie kann man, beginnend bei Cp 1 und dann Coup für Coup, die Ergebnis/Saldenstände in einen damit entstehenden Entscheidungsbaum auszählen, ohne im Datennirvana zu landen. und, leider, 2. wie sinnvoll ist das? Denn das dürfte ja klar sein: wenn sich mit dieser Spielweise keine nutzbaren Muster bilden, kann man sich die Arbeit eigentlich sparen. Und umgekehrt: wie will man wissen, daß sich keine nutzbaren Muster bilden, wenn man nicht nachschaut. Wie so oft, läßt sich das mit Rechnen nicht auflösen. Frage 1 taucht immer wieder auf, die vereinfachte Kurznotation hilft in diesem Fall schon deutlich, und dennoch bleiben noch zu viele Möglichkeiten; das ist übrigens weniger eine Frage des Programmierens als eine des Möglichkeitsraumes und der damit verbundenen zu bewegenden Datenmassen - und deren Aussagekraft. Beim Betrachten der Möglichkeiten für Coup 1 bin ich, wie Du, auch gleich auf das Erscheinen von Zéro gestoßen. Bei der ersten Auszählung hat mich das nicht gestört, es wird eben stur ausgewertet. Anders bei der feineren Betrachtung: da in Coup 1 nie real gesetzt wird, kostet Zéro hier auch nichts; ein Spieler, der real hier einfach weiter macht, verliert jedoch mit jedem folgenden Coup die Möglichkeit auf noch höhere Gewinne. Da erscheint es mir klüger, Zéro im ersten Cp einfach zu streichen, und zu postulieren, der Beginn der 10er-Sequenz, also Coup 1 muß immer NichtZéro sein. Noch klarer wird es beim bspw. fünfmalig ununterbrochenen Erscheinen von Zéro in Cp 1-5: Cp 6 kann dann die erste TS bringen, uns bleiben höchstens 4 real spielbare Cps, wie soll sich da die Kraft der Spielidee entfalten? Gruß elementaar
-
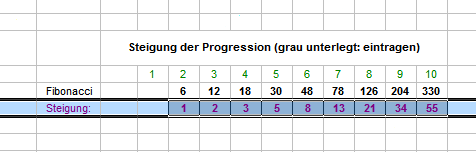
Die Auswertungstabelle habe ich etwas weitergeführt. Im Blatt "Testmaske" kann man jetzt, Zeile 39 unter dem Alarmblock, zentral eintragen, wie stark die Progressionssteigung sein soll. Hier bitte nur die grau unterlegten Felder mit dem einfachen Stückwert füllen. Beispielhaft habe ich die von Egoist angedachte Fibonaccifolge eingetragen. Mit dieser reduziert sich der maximal mögliche Gewinn auf +1.100 Stück (vor Differenzsatz) das größte Minus bleibt bei -38. Die beiden Auszählungsblätter fehlen in dieser Datei logischerweise, da für variable Steigungen nicht mehr gültig. Gruß elementaar TS_PlusProgression_Egoist_05_F.xls
-
Guten Morgen Egoist, hoffentlich geht es dem Arm besser?! Deinen Vorschlag zur vereinfachten Kurznotation finde ich sehr gut, und bin sehr dafür, daß wir das zukünftig so machen. Deine Ahnung kommender Eisheiliger (im nicht meteorologischen Sinn) scheint sich in so fern bestätigt zu haben, als die Quote der Endsalden in Cp 10 >=0 mit gut 32% niedriger ist, als auch ich mir erhofft hätte. Allerdings setzt das auch einen Spieler voraus, der sich mit dem Ergebnis, (wahrscheinlich) auf 10 so gespielte Coups nie mehr als 38 Stücke verlieren zu können, zufrieden gibt, und hinfort nicht nach links und nicht nach rechts schaut und immer 10 Coups bis zu Ende spielt. Nun denn, einem solchen Spieler haben wir immerhin mit der Untergrenze helfen können. Für mich viel interessanter bei dieser Untergrenze ist allerdings weniger deren absolute Höhe, als vielmehr die Frage: was muß passieren, damit diese Untergrenze erreicht wird. Und da scheint mir um vieles Bedenklicher, nachdem, was wir bisher zusammen getragen haben, daß der Maximumabsturz um Cp 4, 5 noch nicht wirklich erkennbar ist. Gewiß, daß eine solche Partie nicht gut läuft ist klar, die Hälfte der Partie ist auch schon gespielt, es kann aber auch noch zu einem versöhnlichen Ende kommen. Und andererseits scheint eine solche Überlegung für eine "Gewinn-"progression doch sehr "system-"fremd: ist das nicht das normale Verhalten eines solchen Vorgehens? Das bewußte Hinnehmen zahlreicher möglichst kleiner Verluste, um bei wenigen Gelegenheiten alles wieder rauszureißen? Damit wäre die Beschäftigung mit der maximalen Verlustgrenze zwar wichtig, und ja auch relativ einfach auszuführen, für den Ansatz jedoch der allerkleinste Teil; die Untersuchung der gewinnenden Spielabschnitte ist wesentlich umfangreicher aber auch das "Eigentliche" Deiner Idee. Mal sehen, was uns dazu einfällt. Gruß elementaar
-
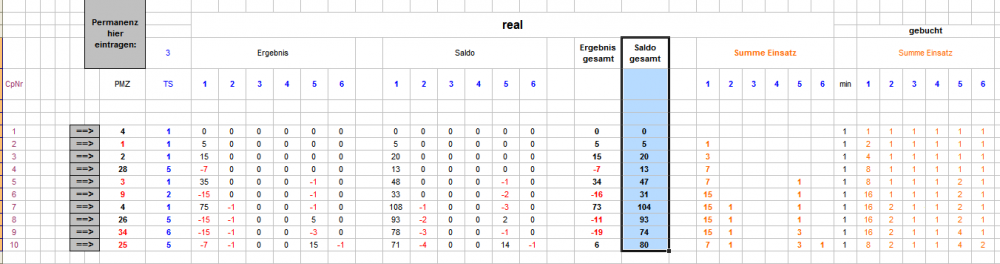
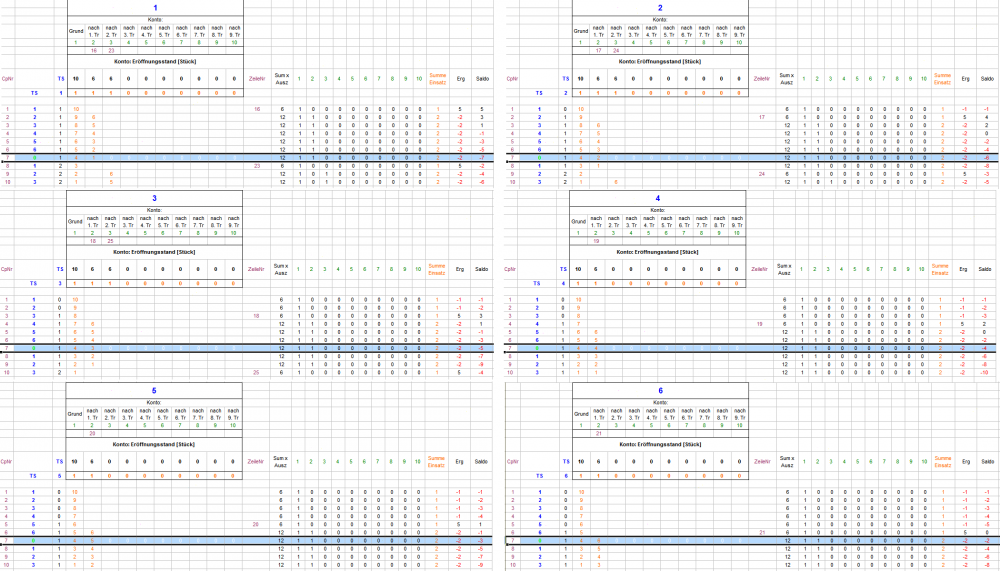
Guten Morgen onedin, Bei mir auch! (Hier allerdings an ein Wunder zu denken, erscheint dann doch unangemessen). Bei einer Gegenprüfung über die sechs TS-Blätter ist mir kein Fehler aufgefallen. Besonders bei TS1 kann man aber sehr schön die Wirksamkeit der "Nachrückerregel" studieren. Der eingebaute Automatismus, daß nach anfänglichen Treffern zwar ordentlich stärker gefeuert, selbst bei weiteren Treffern aber auch an Kapital- und Gewinnsicherung "gedacht" wird, ist brillant. Da das "richtige" Verhältnis zu finden ist schwierig - viel weiter oben, stellte Egoist ja schon einmal die bange Frage, ob nach dem 4. Treffer tatsächlich die gesamte Auszahlung zum Befüllen des nächsten Kontos verwendet werden soll -, es kann sich aber durchaus herausstellen, daß das jetzige Vorgehen schon das Optimum ist. Gruß elementaar
-
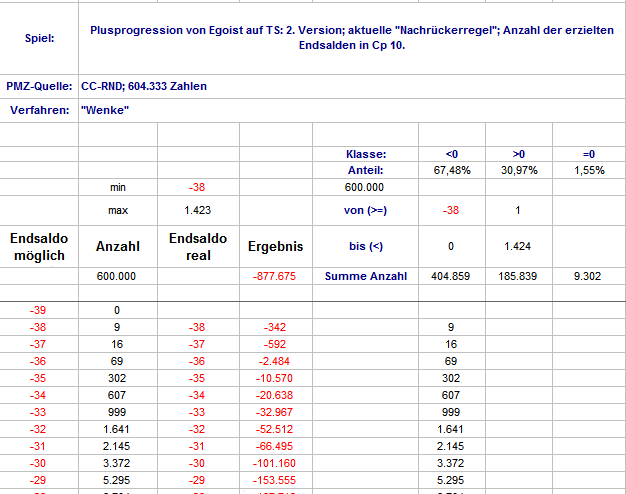
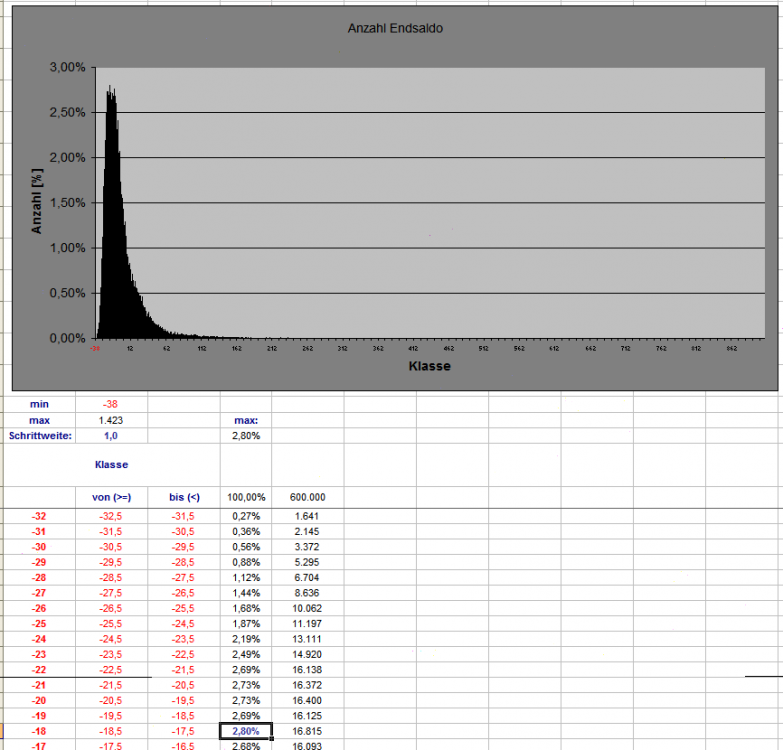
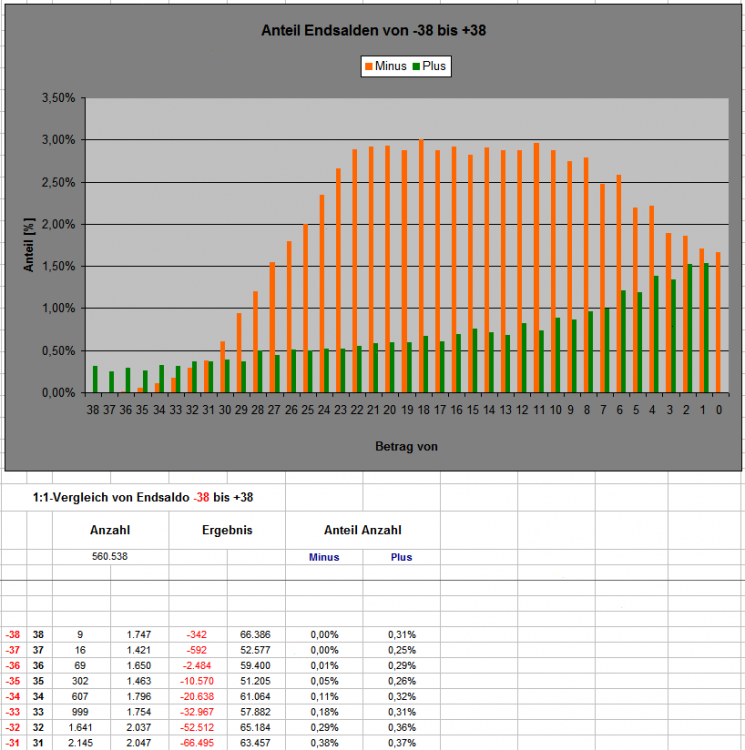
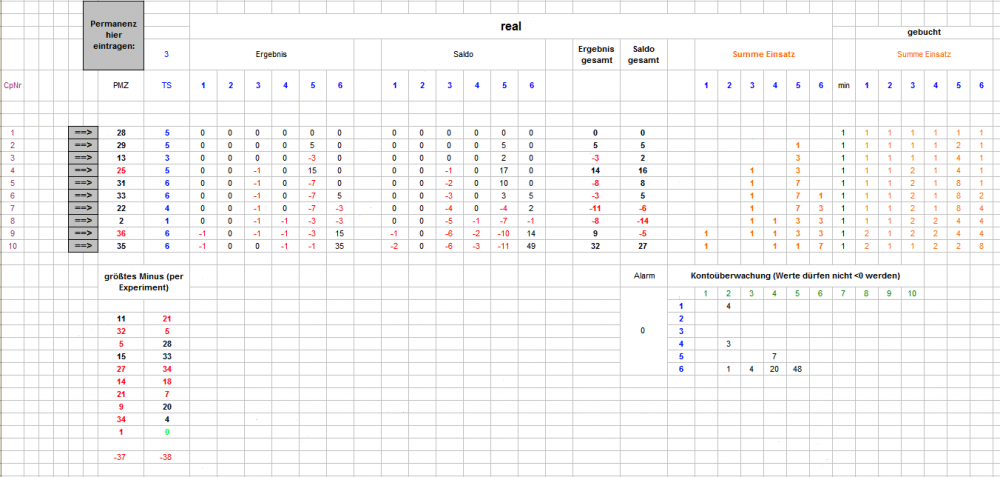
Hier kommen Neuigkeiten aus der Zählhütte: Mit Verfahren "Wenke" und 604.333 RND-Zahlen wurden Permanenzstrecken von je 10 Coups erzeugt. Diese wurden im Differenzsatz mit "Nachrückerregel" (soweit, wie bisher implementiert) bespielt. Der entstehende Endsaldo (also Gesamtergebnis in Cp 10) wurde sodann in der Werteliste als Anzahl notiert. Die Werteliste habe ich in Einerschritten von -50 (als Minimumwert) bis +2.225 (als Maximumwert) angelegt. Dieses Verfahren habe ich 600.000 mal wiederholt (es wurden also 600.000 x 10 = 6.000.000 Coups bespielt). Falls nun jemand enttäuscht ist von dem Versuchsaufbau (damit werden sich nicht viele Fragen klären lassen), dem kann ich in der Sache zwar zustimmen, gebe aber zu bedenken: - in dieser frühen Phase, ist ein Grund für Spezialisierung noch nicht gegeben, z.B. ist die Frage, wie steil die exponentielle Entwicklung der Trefferkonten sein soll, noch in der Diskussion. - naturgemäß überwiegt zur Zeit noch das Nichtwissen über das Verhalten des Spiels - da klein und bescheiden anzufangen, ist nicht die schlechteste Strategie, auch wenn sich später herausstellt, daß manches unnötig war, oder hätte zusammengefaßt werden können. - der momentane Stand meiner persönlichen Leistungsfähigkeit - lieber (hoffentlich richtig) gelöste Miniaufgaben als Umfangreicheres mit Fehlern. Hier die Datei: TS_PlusProgression_Egoist_04_F.xls Sie entspricht der ersten Tabelle ...03_F plus die Neuigkeiten. Im Blatt "Auszählung Endsaldo" sind in Spalte A die möglichen Endsaldowerte aufgeschrieben, in Spalte B die gefundenen Häufigkeiten. Spalte C blendet die Anzahl "0" der Endstände aus. Spalte D multipliziert Saldoendstand mit Anzahl. Die Extremwerte zeigen mal wieder, warum sie so heißen: das größte Minus mit Saldoendstand -38 Stück wurde 9 x verzeichnet, das Maximum war mit erzielten +1.423 Stück ein mal erreicht, das zweitgrößte Plus von einmal +909 Stück hält einen gehörigen Respektabstand. Das Blatt "Verteilung_01" zeigt das Verteilungsdiagramm mit der Schrittweite "1", durch den großen Möglichkeitsraum erwartungsgemäß mit kleiner Aussagekraft. Der Hochpunkt ist mit 2,80% bei Saldoendstand -18, immerhin 9.302 mal (1,55%) wurde ein Endstand von "0" verzeichnet. Wiederum im Blatt "Auszählung Endsaldo" habe ich eine Gegenüberstellung der Endsaldobeträge von -38 bis +38 gemacht. Insgesamt sind damit schon 560.655 Ereignisse erfaßt! Das Diagramm zeigt die anteiligen Prozentwerte. Zu Weiterem bin ich noch nicht gekommen, man kann noch einiges mit den Daten anstellen (z.B. wer möchte, im Blatt "Auszählung Endsaldo" nach Spalte G neue Spalten einfügen und durch kopieren von Spalte G weitere Klassen erzeugen und durch eintragen in Zelle 27/28 deren Grenzen festlegen). Für heute mache ich jetzt mal Pause! Gruß elementaar
-
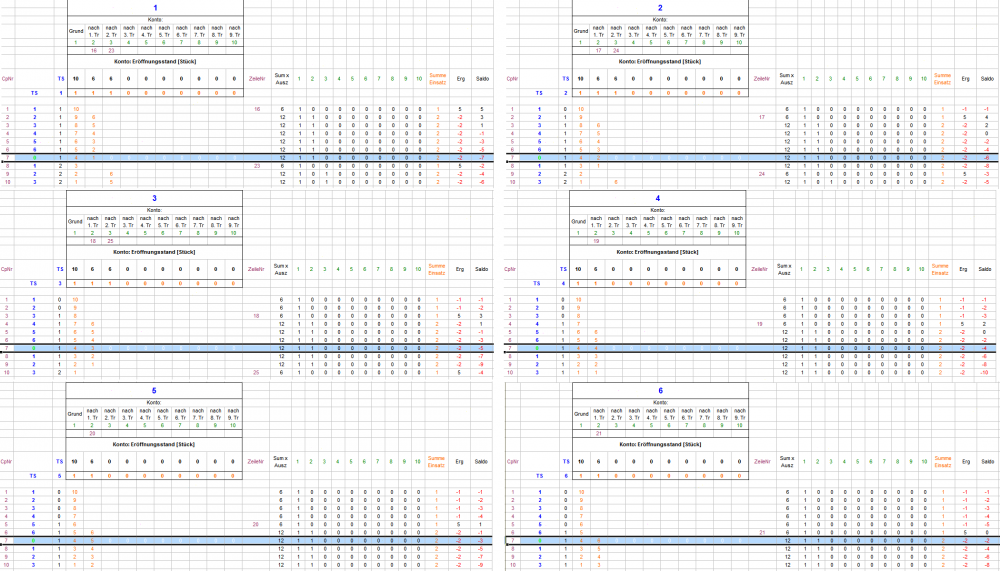
Hallo Egoist, vielen Dank für die erläuternde Entwarnung. Das soll Dich aber, bitte, auf keinen Fall hemmen, über jede, auch nur vermeintliche, Unstimmigkeit Kunde zu tun! Zumindest ich halte gesichertes Wissen, ungeachtet der aufzuwendenden Mühe, für erstrebenswert, eindeutiger umgekehrt zu formulieren: ungenau arbeiten ist Zeitverschwendung. Ich schicke dann mal den neuen Versuch der Massendatenerfassung der Endsalden los. Auch gestern, beim Probelauf, kam ich in Sachen ultimative Verliererstrecke nicht unter -38 Stück. Ein Beispielpermanenzverlauf ist ja unter "GrößtesMinus" in der Testmaske verzeichnet. Demnach scheint es so zu sein, daß es unter Verliereraspekt günstiger ist, wenn eine TS im Mittelteil zwei mal trifft, damit sie im Folgenden genügend lange 4 (differenzbereinigt: 3) Stück setzt und verliert (5 x -3). Im Beispiel "33", "34" als Doppeltreffer in Cp 4 und 5. Läßt man diese beiden nur einen Coup nach oben wandern (um noch ein sechstes Mal -3 zu provozieren (die "28" aus Cp 3 jetzt in Cp 5), stellt man fest, das der Endsaldo auf -32 gestiegen ist, weil in Cp 10 durch Differenzsatz wieder 0 Stück real gesetzt werden. Bin mal gespannt (weil zu geistesschwach, es von Hand auszupröbeln) ob die Simulation die -38 noch unterbieten kann. Sollte dies geschehen, lasse ich die betreffende Zahlenfolge aufschreiben. Gruß elementaar
-
Hallo Egoist, Da bin ich jetzt, leider, ziemlich verwirrt und bitte um Abhilfe, obwohl mir Dein Text ja wünschenswert klar erscheint. Vielleicht schaffen wir mit Schritt-für-Schritt-Vorgehen (wie es oben schon prima funktioniert hat) Klarheit: Bis gefallenem Cp 6 dürfte alles klar sein. In Cp 7 fällt Zéro. Alle TS verlieren gebucht 2 Stück, der Differenzsatz bewirkt, das diese Zéro uns nicht real 12 Stück kostet. TS1 hat damit sein Gewinnkonto (KontoNr 2 in der Tabelle, nach dem 1. Cp) erschöpft (6 x 1 Stück in Cp 2-7), setzt also in Cp 8 nur 1 Stück aus seinem 10-Stück-Grundkonto. TS2 bis TS6 haben jeweils noch mehr Munition und spielen gebucht je 2 Stück in Cp 8 - per Differenzsatz 1 Stück auf TS2-6, TS1 kein Satz. In Cp 8 trifft wieder TS1 und kann ein neues Gewinnkonto mit gebuchten 6 Stück Auszahlung befüllen, dafür hat jetzt TS2 sein Gewinnkonto (aus Cp 2, gebuchter Satz 6 x 1 Stück in Cp 3-8) erschöpft, ist also in Cp 9 nur noch gebucht mit 1 Stück aus seinem Grundkonto dabei. Das von mir im Zitat fett Markierte ist also gegeben, und ist, meiner Meinung nach, ja eines der Highlights der Spielweise. Ich bin vielleicht zu vernagelt, aber wo genau Du den Widerspruch zu Deinem Konzept siehst, kann ich im Moment nicht erkennen. Ich muß da um weitere Erläuterung bitten - vielleicht kannst Du mich erleuchten. Gruß elementaar
-
Hallo Egoist, "der heute seinen Mausarm kaum benutzen kann..." Das ist betrüblich zu lesen. Und hoffentlich ist es nicht dieses gräßliche Schulterentzündungsdingens (SEHR schmerzhaft, ca. drei Wochen nur im Sitzen schlafen, außer Abwarten bis es weg ist keine wirksame Abhilfe; da hat man lange Freude dran). Mein herzliches Mitgefühl und gute Besserung! Allerdings demonstrierst Du mit Deinen Beiträgen in dieser Situation Steherqualitäten - und dafür meinen doppelten Respekt. Also bei einem teilweisen Neuansatz vom Mich wäre ich sofort dabei, da sammelt sich mit den Jahren beim eigenen Verhalten doch einiges an, wo man denkt: "muß das jetzt wirklich so sein?" Und diese Änderungswünsche müssen ja dann zeitaufwändig trainiert werden, damit man sich darauf verlassen kann - ein paar geänderte Codezeilen im Betriebssystem wären der deutlich weniger mühsame Weg. Aber natürlich: Dank für Lob und Preis! Das würde ich dann aber doch eher nicht dem unterstellten Hirn zurechnen: wer, wie Du es getan hast, und das nicht zum ersten Mal, an einem Abend eine Spielidee von solcher Eleganz und Finesse zusammenwürfelt, muß sich, aus meiner Sicht, da gar keine Gedanken machen; es scheint, leider, eher Folge meiner Holzhackermethoden (also eine ganz unbeabsichtigte Obfuskation) - im besten Fall sind sie klarer nachvollziehbar als die wahrhaft elegante Lösung, überwiegend jedoch stehen sie unter dem Dauerverdacht: "das kann man deutlich einfacher, ressourcenschonender und effektiver machen". apropros Obfuscator: nächsten Sonntag ist wieder weltweiter Lochkameratag, da mitzumachen oder auch nur die Ergebnisse der Teilnehmer zu betrachten, ist deutlich freudvoller als sich mal wieder mit den Nickligkeiten dieses Programms herum zu schlagen. Gruß elementaar
-
Hallo coocie, Das ist kulinarisch wertvolle Roulettesimulation! Dicke Bohnen sollte es ja auch mindestens in drei verschiedenen Farben geben, Kichererbsen und Linsen sind in Eintöpfen ebenfalls schmackhaft; letztere verhalten sich allerdings bei der Stapelsimulation ziemlich unkooperativ. Das ist sehr deutlich nahrhafter als meine öde Tastaturbedienerei - viel Vergnügen! Gruß elementaar
-
Hallo Egoist, bei der Fehlersuche war ich recht schnell erfolgreich (wie so oft, innerhalb einer umfangreichen Formel ein falscher Bezug). Durch dieses Vorkommnis gewarnt, habe ich in den TS-Blättern sowie der Testmaske eine Kontoüberwachung installiert, damit kein Konto mehr ausgeben kann als es noch Kredit hat. Will ein Konto jetzt mehr ausgeben, als es zur Verfügung hat, färbt sich die betreffende Diffenrenzzelle knallrot. In der Testmaske gibt es die Zusammenfassung der TS und ein Alarmfeld, welches sich mit "Rot" meldet, falls ein Konto sich übernimmt. Alle Interessierten bitte beachten: die alte Datei TS_PlusProgression_Egoist_01.xls NICHT mehr verwenden, sie enthält Fehler! TS_PlusProgression_Egoist_03_F.xls Ein Testlauf über 10.000 Partien löste dabei keinen Alarm aus; dieser Fehler sollte also behoben sein (Zukunft wie immer ungewiß). Bei der von Dir gespielten Permanenzstrecke finden sich jetzt auch Deine Angaben wieder. Endsaldo dieser Partie ist +27 Stück. Vielen Dank nochmal für das Aufspüren des Fehlers! Für heute höre ich jetzt aber wirklich auf Gruß elementaar
-
Hallo Egoist, das nenne ich Sportsgeist! War hoffentlich angenehm. Nein, an der Sonne liegt das nicht, da hast Du wirklich einen Fehler gefunden. Sehr gut! (Leider ist dadurch die Saldoendstandauszählung obsolet geworden - aber lieber jetzt als noch später). Aber erst durch Dein Schritt-für-Schritt-Schildern für coocie habe ich nicht nur gesehen sondern auch begriffen. Jetzt muß ich mal schauen, wie ich den beseitige. Da schon ziemlich ermüdet, kann das aber bis morgen dauern! Ich melde mich mit der verbesserten Datei - bis dahin: einen schönen Abend noch! Gruß elementaar PS.: Der Abend wird ja noch schöner. Zum Wohlsein!
-
@Egoist hat einen Fehler in meiner Auswertungstabelle entdeckt, deshalb sind die eigentlich hier stehen sollenden Auswertungsdaten fehlerbehaftet.
-
Hallo Egoist, Das ist ja ein überaus netter und würdiger Abschluß des Vorfalls. Glück, daß Du nicht gezögert hast, den Notarzt zu verständigen. Gruß elementaar
-
Hallo PinkEvilMonkey, Das ist ein sehr schönes Kompliment und mich zumindest freut es. Danke! Seit der Vorstellung suche ich ein besser charakterisierendes Wort für Egoistens Vorschlag, Du hast es gefunden. "Elegant" ist auch mein Eindruck, und allein schon deshalb einer näheren Betrachtung wert. Danke auch hierfür. Gruß elementaar
-
Hallo wiensschlechtester, sei herzlich bedankt. Aber gleich die Marathonsitzung! Deine Nachricht an Egoist las sich auch etwas mitgenommen. Gute Erholung! So ist das mit dem Licht der Aufklärung: was eben noch so verheißungs- wie geheimnisvoll klang, ist für mich jetzt doch etwas entzaubert - nein, ich klage nicht, ich habe es ja so gewollt. Den betreffenden Berufsausüber, so er denn von dem von Dir finanzierten Luxusurlaub überhaupt wiederkehrt, vor der nächsten Sitzung mit meinen Rateergebnissen zu konfrontieren, könnte sich, je nach Humor, als kontraproduktiv erweisen. Also könnte einem, in dieser Donaustadt, wenn man des Wortgerausches des Gegenübers nicht mehr gewachsen oder sonstwie zu inkommodiert ist, mehr oder minder laut entweichen: "Halt die (oder den?) Pappe(n)"? Gruß elementaar
-
Hallo wiensschlechtester, das ist zwar jetzt sehr weit weg vom Thema - und vielleicht ist es auch ein supergeheimer insider - aber das oben von Dir verwendete, mir gleich sympathische und ohne Frage phantastische Wort "Pappenschuster" hat mein Interesse geweckt. Wer, oder welches Gewerk, könnte damit gemeint sein? Ein Buchbinder? ein Hersteller von Kartonboxen? Eine schnelle ixquick/startpage-Suche erbrachte die Ausbeute von 1 (in Worten: einem!) Link, der aber leider zu einer Fleischerei führt. Daß die da weiterhelfen können, kann ich kaum glauben. Könntest Du, falls in der Lage und gewillt, meiner Unwissenheit abhelfen? Dank im Voraus ist Dir gewiß! Wobei ich hoffe, der "Pappenschuster" ist nicht Teilnehmer beim Kongress der unverstandenen Logikanwender; an die, so mußte ich zu meinem Bedauern lernen, kommt man ja kaum heran. Gruß elementaar
-
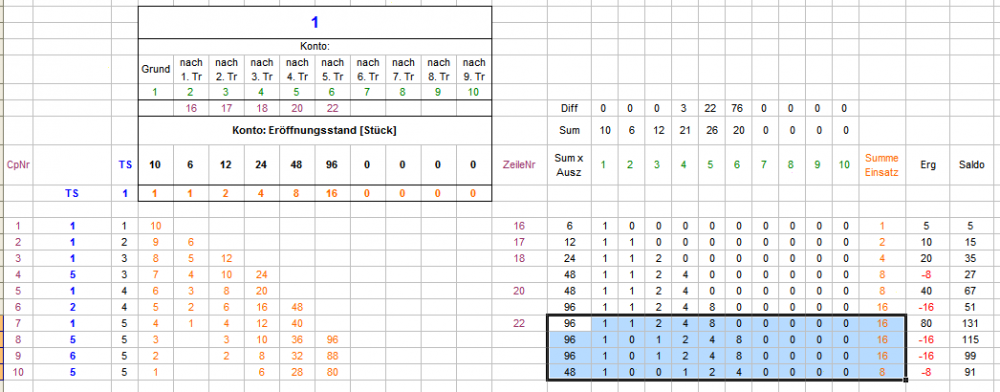
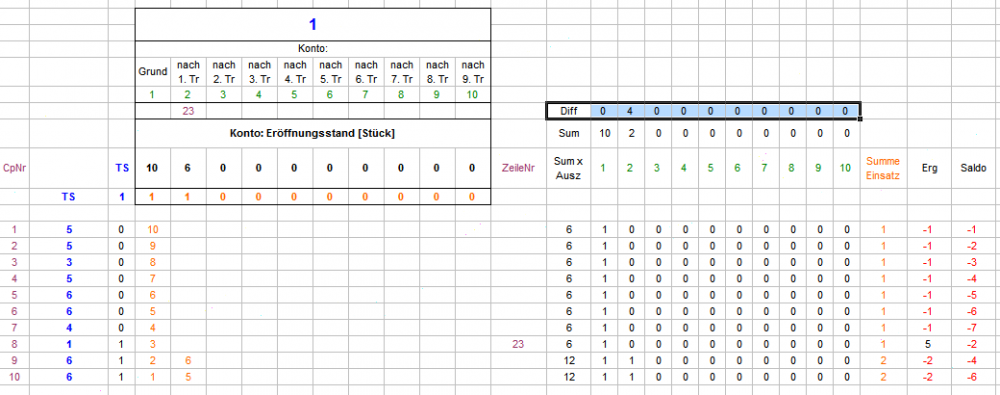
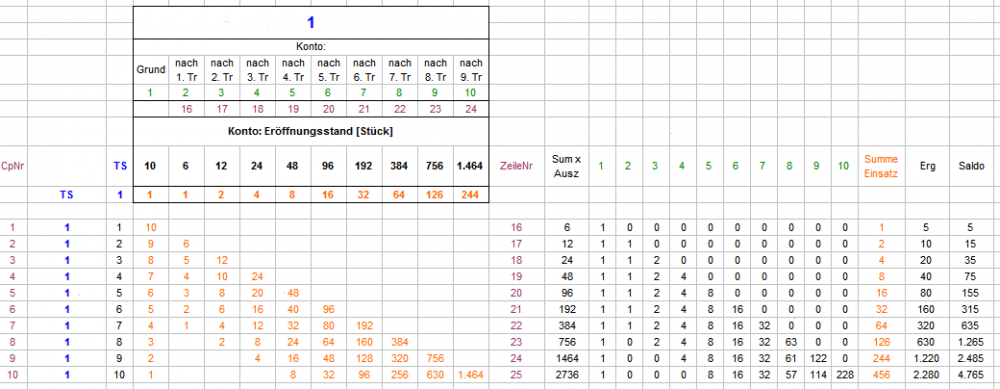
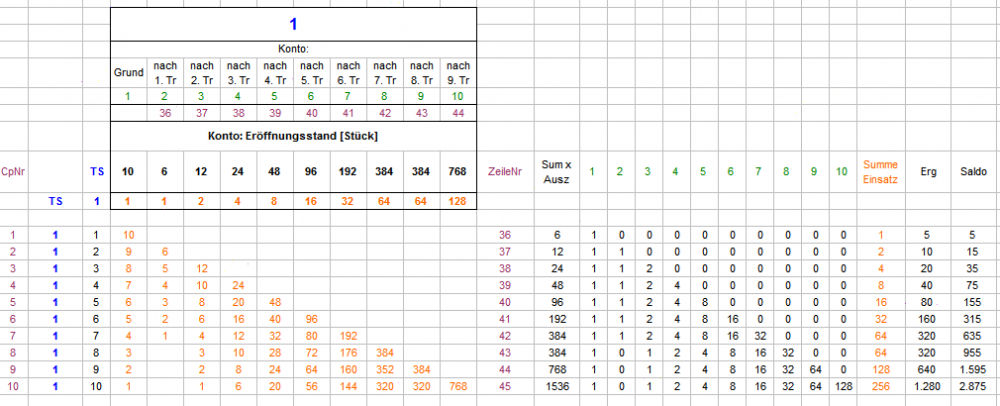
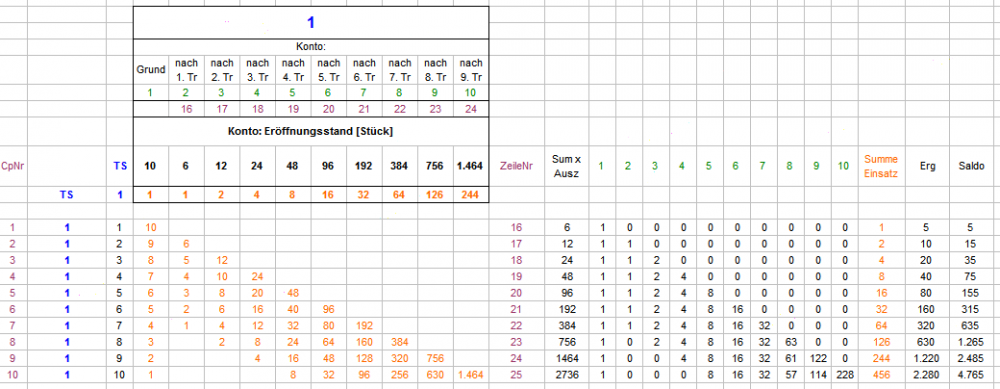
Hallo Papa Maus, Ja, fast. Jede TS wird für sich abgerechnet und jede hat ein Grundkonto von 10 Stück, deshalb: 6 x 10 Stück je 1. Konto pro TS. Da hast Du Recht, da stimmt was nicht - vielen Dank für's Aufpassen. Da muß ich mich mal tüchtig selber ausschimpfen - immer diese vermaledeiten Flüchtigkeitsfehler. Ich versuche, es oben auszubessern. Die von Dir vorgeschlagene Zahlenreihe ist es aber auch nicht, so sollte es jetzt stimmen: Konto 8 (nach dem 7. Treffer) ist das letzte Konto, was gegenüber dem Vorgänger verdoppelt. Für Konto 9 ist der Satz aus Konto 2 (1 Stück) wegen Erschöpfung nicht mehr dabei, für Konto 10 ist auch Konto 3 (2 Stück) Pleite und ausgeschieden. Dadurch flacht die Erhöhung minimal ab. Vielen Dank nochmal für den Hinweis! Gruß elementaar
-
Hallo Papa Maus, die Früchte von Egoistens Frühlingsabend auf der Dachterrasse sind in der Tat beeindruckend und charmant. Dabei sind Einzelheiten durchaus noch im Fluß (alles andere wäre auch deutlich zuviel erwartet). Dabei ist Egoist so eine Art Zauberlehrling, und wir anderen die etwas vorpreschenden Besen. In Deinem Beispiel, sofern ich es verstehe (was nicht zwingend der Fall sein muß), buchst Du, glaube ich, zuviel. Zur Zeit machen wir es so: Die Gesamtauszahlung eines Gewinncoups wird zur Eröffnung eines neuen Kontos verwendet, welches, sofern die Restcoupstrecke reicht, mindestens sechs mal mitsetzen soll (Auszahlung / 6 = Stück pro Satzcoup). Ohne "Nachrückerregel" (weiter oben beschrieben) sieht die 10-Trefferserie dann so aus: Mit "Nachrückerregel" so: Durch den Differenzsatz sieht die Gesamtbilanz dann so aus: Gesehen, geschweige erlebt, habe ich eine Zehner-Trefferserie auf TS allerdings noch nicht. Der Rat von Egoist, Jetons (oder Kekse oder Trockenerbsen (allerdings schlecht stapelbar)) pro Konto und TS physisch vor sich aufzubauen, ist zum leichteren und besseren Verständnis sehr zu empfehlen. Gruß elementaar
-
Hallo Egoist, vielen Dank für Dein Mitgefühl. Und was Du schilderst, macht wieder deutlich, je nach Mensch und Heftigkeit der allergischen Reaktion, ist damit nicht zu spaßen - und, fallweise, mehr als ein bißchen Niesen und Augentränen. Es ist halt jedes Jahr derselbe Mist, mal schlimmer, mal weniger schlimm.; man muß halt irgendwie mit dem zurecht kommen, was man nicht ändern kann. Übrigens: beim Fehlerentdecken ist zumindest bei mir ein um Entschuldigung Bitten wirklich nicht nötig - darum geht es ja beim öffentlichen Diskutieren, je mehr Fehler auf diese Weise aufgedeckt und verbessert werden können, umso besser. Wäre ja schade um die Zeit, wenn Simulationen stundenlang mit fehlerhaftem Gerät liefen und am Ende wertlos wären. Also nur zu! Ich habe gerade Deine Killerperm eingegeben, und der Nichtsatz in Cp 7 entsteht durch den Differenzsatz: alle TS hätten hier 2 Stück zu setzen; zusammen also 0. Das so etwas vorkommen kann, macht mir Deine Idee u.a. besonders interessant. @suchender verliert hier in Cp 7 12 (=6 x 2 Stücke) Bis demnächst! Gruß elementaar