elementaar
Mitglieder-
Gesamte Inhalte
1.441 -
Benutzer seit
-
Letzter Besuch
Inhaltstyp
Profile
Forum
Kalender
Articles
Alle erstellten Inhalte von elementaar
-
Roulette-Turnier 2024
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Und jetzt auch noch ein Ausflug in die Sprache der Diktatur. ER lässt wirklich nichts aus. Was "Kleinigkeiten" sind, bestimmt selbstverständlich ER, und nur ER, und das auch noch fallweise. Dann tauchen nicht existente "32"-er auf, weil ER sie hingeschrieben hat, für SEIN hochgestochen "Analyse" genanntes Geschwafel: Kleinigkeit. "Treffer" mit Tripelbedeutung: Kleinigkeit. X-fach nachgewiesene Logikfehler: alles Kleinigkeiten. Herbeiphantasierte Glocken, Mittelwerte, "Topperformance", Kleinigkeiten noch und nöcher. In irgendeinem SEINER Texte nicht auf derlei "Kleinigkeiten" zu stossen, erfordert vollständige Blindheit. Da sind Rechtschreibe- oder Rechenfehler wirklich die kleinsten "Kleinigkeiten", aber selbst diese weigert ER sich in SEINER bornierten Faulheit zu verbessern. -
Roulette-Turnier 2024
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Wie immer: statt einer Antwort der nächste Dreck. Mit dem gleichzeitig SEINE Unfähigkeit selbst zur einfachsten chronologischen Unterscheidung deutlich wird. Wenn es so wäre, wie von IHM behauptet, dann hätte das "Erfolgserlebnis" gegen "Lebensfrust" mit dem Hinweis auf SEINEN Fehler schon statt gefunden. Danach ist die Korrektur sofort möglich. Warum führt ER sie nicht aus? Warum statt dessen Beschimpfung? Und noch gesteigert: "ist zwar falsch, aber, weil von MIR, selbstverständlich wahr"? -
Roulette-Turnier 2024
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Und selbst wenn es so wäre - warum korrigiert ER SEINE Fehler nicht sofort? Statt dessen geisteskranke Beschimpfungen und "ist zwar falsch, was ich schrieb, aber weil ich es schrieb, ist es wahr". Bescheuert! Und wann kümmert ER sich mal, schon beim Eintippen SEINER Dreckschleudern, um die rote Unterkringelung, die automatisch im Eingabefeld erscheint? Ist das schon zu viel verlangt an Sorgfalt? Was ER hier jeden Tag abliefert, spiegelt ja nicht nur die Verachtung jeden Lesers, ER selbst hält offensichtlich von SEINEN Verlautbarungen (zu Recht) so wenig, daß selbst dieses bißchen Sorgfalt und selbst in SEINEN eigenen Augen offensichtlich verschwendet ist. Für IHN und SEINE "Texte" gilt wirklich der alte Kinderspruch: "Wer das liest, ist doof". -
Roulette-Turnier 2024
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Was hat der Hinweis auf einen SEINER offensichtlichen Rechtschreibefehler mit "Schlauheit" zu tun? Was mit Klugscheißerei? Was damit, daß @Hans Dampf (von) angeblich irgendeine Wirkung erzielen will? Jetzt mache ER aber wirklich mal einen Punkt und atme durch. Äpfel sind keine Birnen und beides sind keine Würstchen. Das ist einem Kleinkind klar, sobald es der drei Sachen zum ersten Mal ansichtig wird. Wenn das SEIN Maßstab für "Schlauheit" sein soll, dann muss ER aber noch unglaublich viel "schlauer" werden, bevor ein Gespräch mit IHM überhaupt möglich würde. Aber dafür ist ER ja, wie seit viel zu langen Jahren demonstriert, zu faul. "Lächerlich" ist in diesem Zusammenhang ein Euphemismus. -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Hoffentlich sieht das der "math. " nicht. Der regt sich als erstes über den verwendeten Punkt statt eines Kommas auf. Falls er darüber hinweg kommt, streicht er als zweites (bi) die erste Nachkommastelle "extra", damit es dann 98,2 (bi!) heißt. Dann rätselt er, wieso die Maßeinheit [m] ist, wo es doch [n], wie in bin, sein müsste. Dann kommt das Irrenhaus auf Wandertag vorbei, und fragt nach dem Weg zu den schönsten Glockenklängen. Das kann dann schnell zu viel (multi) werden. -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Fassen wir zusammen: Treffer = Erscheinen einer Zahl ( d.h. sie wurde in ihrem Fach von einer Kugel gemeuchelt) Treffer = Satz des Spielers auf eine Zahl, die nachfolgend auch erscheint. Treffer = Zahl, die weder erscheint, noch gesetzt, sondern in SEINEN Aufzeichnungen "verzeichnet" wurde, und deshalb per realer Nichtexistenz wertvolle Informationen zur Analyse beiträgt. Pasta! Alles ganz einfach. Wie immer: der ewig Unverstandene wird von den "Dillitanten" (wo sind die Onkel abgeblieben?) "gemoppt". Klarer Fall zum Glocke schlagen: BIN-Boing. -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
Es liegt mir fern, etwas Anderes auch nur anzudeuten, da ich zu einer themenbezogenen Diskussion praktisch nichts beizutragen habe. Falls es dennoch nicht so gewirkt hat, bitte ich um Entschuldigung. -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
Zumal: https://www.roulette-forum.de/topic/31194-eine-frage-zu-reihen/page/2/#comment-517045 Aber erfreulicherweise kann ja jeder spielen, was er will. Viel Vergnügen! -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
Hallo @chris161109, es freut mich, wenn meine "Fleißarbeit" Dich dazu animiert hat, noch einmal einen längeren Text zu verfassen. Das ist sehr schön. "Penneys Game ist schön, macht aber viel Arbeit". Das ist aber nicht weiter schlimm. Bei temporär eingeschränkten Geisteskräften hilft die Ochsentour meistens weiter. Das Beruhigende der Auszählungen ist für mich, daß man vorher weiß, daß am Ende ein Nullsummenspiel herauskommen muss. Bei scheinbar widersprüchlichen Zahlen klärt man dann zuerst, ob es eine "Fata Morgana" ist, und wenn nicht, auf welche Art und Weise sich das Nullsummenspiel vollzieht. Hier kann es zuweilen interessant werden. Die dabei, immer mal wieder, zu beobachtende Trägheit im Ergebnisverlauf ist ebenfalls bemerkenswert. Deiner resümierenden Aussage, zusammen mit "Kreuzworträtsel"- @Hans Dampf (von), kann ich nur zustimmen. Ein Gewinn im Roulettespiel ist im Verlauf der Permanenz zu finden. Das sollte eigentlich auch dem Letzten klar und damit Allgemeinwissen sein. Wie ich Deinem Text und der Datei entnehme, konntest Du die Interpretationsstränge auf zwei reduzieren - das ist ein schöner Erfolg und zeigt, daß selbst nach jahrzehntelanger Beschäftigung ab und zu Neuigkeiten zu entdecken sind. Glückwunsch! Gruss elementaar -
Eine Frage zu Reihen
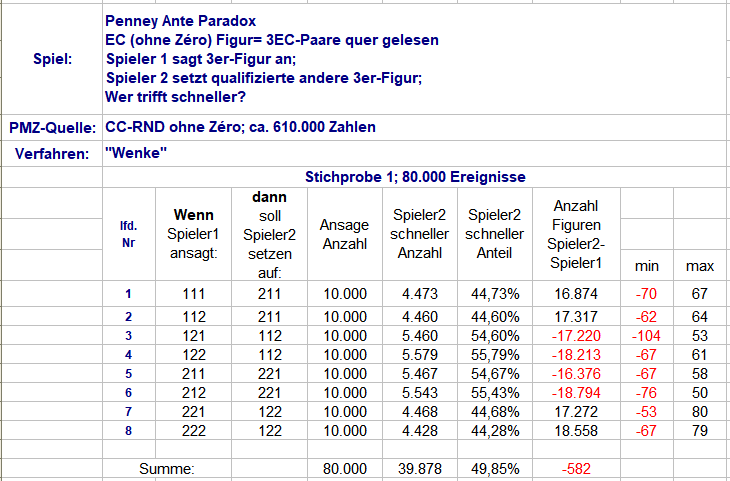
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
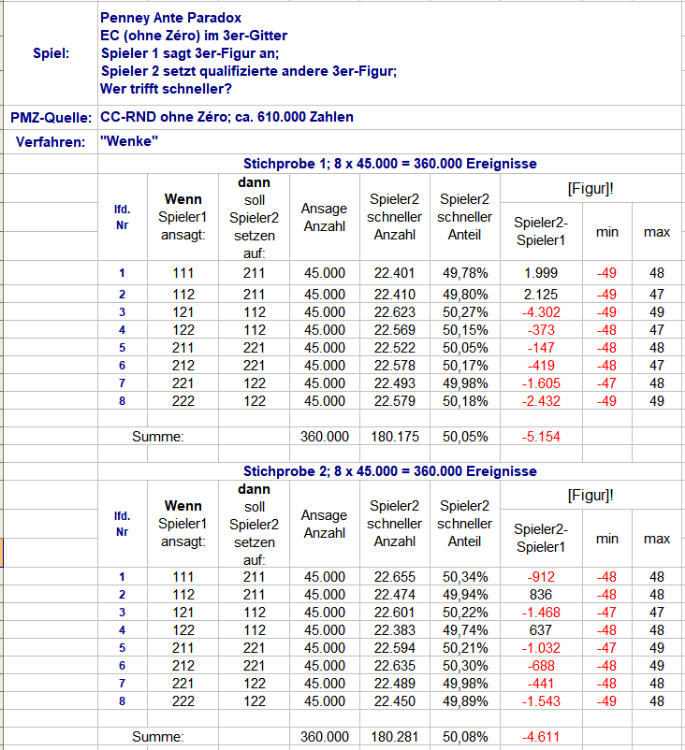
Wie weiter oben schon demonstriert löst sich das Paradox sofort auf, wenn man dafür sorgt, daß sich die Figuren vollständig unabhängig von einander bilden. Dies geschieht, wenn man ein Gitter in Figurenlänge anlegt, oder wenn man die drei EC-Paare quer liest: in jedem neuen Coup (in jedem neuen Gittersegment) bildet sich unabhängig von einander eine von acht Figuren. Die Schnelligkeitsunterschiede in obiger Tabelle erklären sich aus den unterschiedlichen Chancengrößen: viermal fünf gegen vier Zahlen, und viermal vier gegen fünf Zahlen. Hinzu kommen noch die natürlichen Schwankungen, wie die Tabelle im 3er-Gitter zeigt: Ist die Gleichwahrscheinlichkeit der acht zu vier Figuren nach je 45.000 Ereignissen schon recht stabil abgebildet, unterliegt die Frage nach dem "wie viel schneller" auf dieser Prüfstrecke extremen Schwankungen (vgl. bspw. lfd. Nr 1 in Stichprobe 1 und 2). Es bleibt festzuhalten: Penneys Paradox stellt sich nur dann ein, wenn sich die Figuren chronologisch entwickeln. Jede erspähte Figur kann dann im nächsten Coup nur zu zwei von acht Figuren werden. Wirklich spielwirksam können die verifizierten Schnelligkeitsquoten nur genutzt werden, wenn es gelingt, die Satztätigkeit sowohl von Spieler1 wie Spieler2 auf +1 und 0 zu reduzieren (der schnellere bekommt den Punkt, egal was es ihn unterwegs gekostet hat). Gruss elementaar PS: Vielen Dank an @Hans Dampf (von) für den Zwischenzuspruch. -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
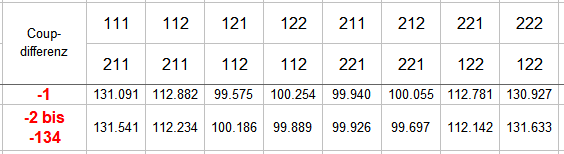
Um den obigen 43,70% zu 37,63% Zahlenzauber möglichst schnell aufzulösen: Real wird damit ja behauptet eine 3er-Farbserie erscheine deutlich häufiger als eine 2er-Farbserie. Daß dies unmöglich stimmen kann, sollte allgemein bekannt sein. Was ist also schief gegangen? Die Betrachtungsweise. Statt die Werte verschiedener Spalten zu vergleichen, muß man in derselben Spalte bleiben, und den Wert von "-1" mit der Summe von Nicht -1 (=-2 bis -134) derselben Spalte vergleichen. Damit erhält man (annähernd) das erwartete Nullsummenspiel. Gruss elementaar -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
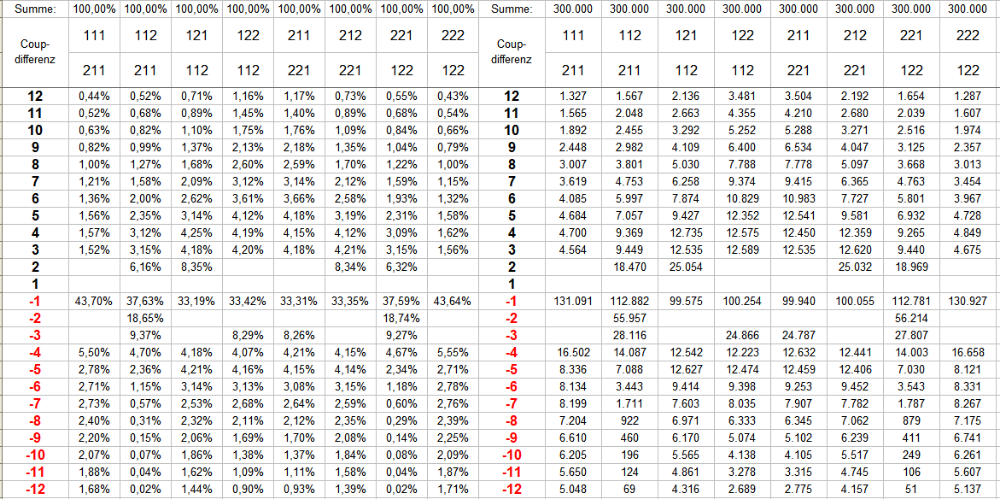
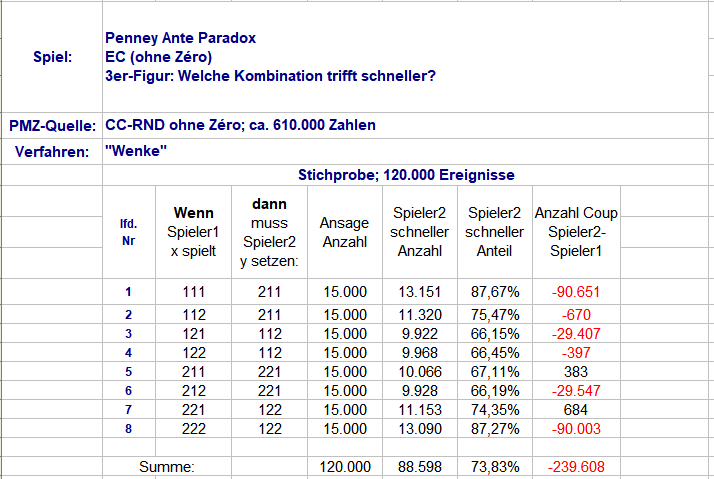
Weil beim Herumspielen mit obigen, summarischen Zahlen doch recht zügig der Wunsch nach einer genaueren Betrachtung entsteht, habe ich mich zur, leider zeitaufwändigem, Auszählung der genauen Schnelligkeitsabstände entschlossen. 100.000 Versuche ergaben über alle drei EC-Chancenpaare zu jeder Figurenkombination 300.000 Ereignisse. In dieser Stichprobe gab es zwei größte Plusabweichungen ("112" war einmal 60 Coups schneller als "211" und "122" war einmal 60 Coups schneller als "112"); der Betrag der Minusabweichung war einmal 134 Coups ("122" schneller als "222"), davor einmal 133 Coups ("211" schneller als "111"). Diese Extreme haben natürlich nur akademischen Wert, illustrieren jedoch noch einmal, welchen Vorteil Spieler2 hat (Abweichung +60 zu -134). Die Ergebnisse in der mittleren Lage sind verwirrend genug: Einen Schnelligkeitsvorteil "0" kann es nicht geben, diese Zeile wurde deshalb weggelassen. Einen Schnelligkeitsvorteil von "+1" kann es ebenfalls nicht geben, weil sich aus keiner der acht Spieler1-Figuren im nächsten Coup eine der vier Spieler2-Figuren bilden kann. Aus "211" bildet sich im nächsten Coup (-1) zwangsweise entweder "111" oder "112", hat sich jedoch "112" gebildet, werden zwangsweise (mindestens) drei weitere Coups benötigt, bis sich "111" bilden kann (-4, aber nicht -2 und -3). Mit diesen Herleitungen lassen sich auch alle weiteren Leerstellen in der Tabelle erklären. Nicht jedoch der Unterschied in der Erscheinenshäufigkeit. Nach "211" bildet sich nach der Tabelle im nächsten Coup (-1) zu 43,70% "111" und nur zu 37,63% "112"! Demnach müsste man nach "211" (ohne unmittelbaren Vorgänger der Spieler1-Figur) immer "1" spielen, und hätte mit 43,70% zu 37,63% recht. Ein Nullsummenspiel ist das so nicht mehr. Obwohl dieses "Dauergewinnsystem" statt eines DIN-A4-Blattes sogar mit nur einer einzigen Zeile auskommt, möchte ich vor der unbedarften Anwendung ausdrücklich warnen. Gruss elementaar -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
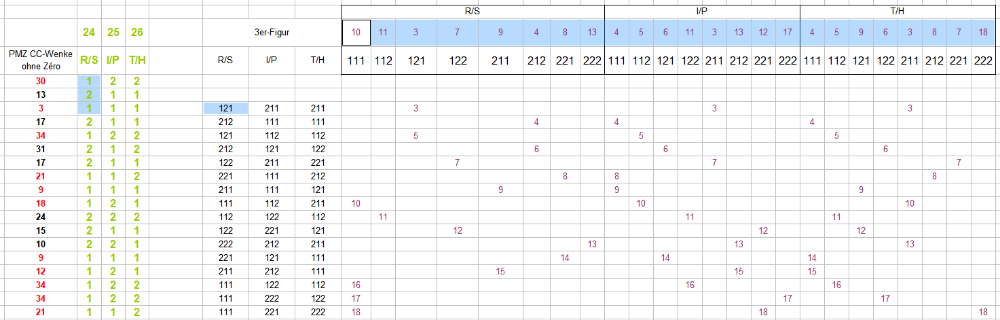
Ganz recht, @Hans Dampf (von), und leider wird es bei weiterer Betrachtung nicht besser. Zu einem anderen Paradoxon heißt es sinngemäß: "wenn man nicht den Verstand verlieren will, befasst man sich besser nicht damit" Damit alle auf demselben Stand sind, wie was gezählt wurde, schildere ich kurz mein Vorgehen (nochmals danke an @Feuerstein), um die in der wikipedia-Tabelle festgestellten Quoten reproduzieren zu können: Abbildung 1 Ganz links die für jede neue Zählung per Verfahren "Wenke" neu erstellte Permanenz. Spalten 24, 25 und 26 schlüsseln die drei EC-Paare auf. Drei Spalten "3er-Figur" bilden daraus die chronologischen Dreierfiguren. Weiter rechts werden, nach EC-Paaren getrennt, das Erscheinen der acht Figuren per Coupnummer erfasst. Deren erstmaliges Erscheinen findet sich in der Zeile über den aufgezählten Figuren. Abbildung 2 Um nicht nur zu Erfassen, welche Figur sich schneller vollendet, sondern gleichzeitig um wie viel schneller, werden danach die Differenzen zwischen den acht möglichen "Ansagen" von Spieler1 und den vier möglichen "Antworten" von Spieler2 gebildet. Über Spieler2 - Spieler1 ergeben sich so die relativen Unterschiede der Figurenvollendung in Coups. Negative Werte bedeuten also Spieler2 war um die entsprechenden Coups schneller, positive Werte bedeuten hingegen, daß Spieler1 mit den entsprechenden Coups schneller ins Ziel kam. Lesebeispiel: Figur "211" vollendete sich auf "R/S" erstmalig in Coup 9, die beiden "Ansage"figuren in Coup 10 und 11 (Abbildung 1) Der Schnelligkeitsunterschied wird folglich für diese beiden Kombinationen mit "-1" und "-2" festgestellt (Abbildung 2) In der Auszählung werden diese Werte addiert; wohingegen bei der "Ob"- und "Wer"-Frage bloß die Anzahl um +1 erhöht wird. Die in der wikipedia-Tabelle genannten Quoten habe ich in Prozentzahlen umgerechnet. Der Befund wurde um eine weitere Stichprobe ergänzt. Wie zu sehen, sind die Schwankungen bei dieser Stichprobengröße noch deutlich sichtbar, jedoch ausreichend eng an den Soll-Quoten, daß man von Reproduzierbarkeit sprechen kann. Ein weiteres Indiz dazu ist die eingehaltene Symmetrie der Figuren 1-4 und 5-8. Gruss elementaar -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
Wie vertrackt dieses Rumspielen mit den befundenen Zahlen ist, mag eine weitere Tatsache verdeutlichen: Wie oben erblickt man "211" und hat sich vergewissert, daß zuvor weder "111" noch "112" erschienen sind (die Bedingung "211" ist "schneller" hat sich also erfüllt), da aber im nächsten Coup nur entweder "1" oder "2" erscheinen kann, sind die im nächsten Coup entstehenden Figuren nach "211" entweder "111" oder "112". Der "Coupvorsprung" von schnellerem "211" sollte also lediglich 13.151 ("211" zu "111") + 11.320 ("211" zu "112") = 24.471 betragen. Und damit weiter betrachtet: nach "211" wird eine der beiden Folgefiguren entstehen und den berechneten Coupvorsprung (von jeweils 1 Coup) erbringen - die jeweilige andere Figur müsste dann den Rest mit 91.321 (Coupvorsprung) - 24.471 (nach dem nächsten Coup) = 66.850 produzieren. Ich fürchte, ich muss mich glatt noch mal "über die Bücher" beugen. Gruss elementaar -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
Hallo @Feuerstein, Dein letzter Beitrag erweckt in mir den Eindruck, als habest Du Penney und seinem Spiel schon den ein oder anderen Gedanken gewidmet. Herzlichen Dank für den reichhaltigen Exkurs. Für den Anbieter eines analogen Jahrmarktspiels ist Penneys Spiel somit eine sichere Bank. Auch mit Roulettezahlen bestätigt sich dies. Wieso auch nicht, sie sind genauso zufällig wie der Münzwurf. Als Neuling in der Betrachtung frage ich mich, bspw. Zeilen 1 und 2 meiner Auszählung, was passieren muss, damit Spieler2 auf 15.000 Ansagen mit 90.651 Coups schneller ist, und dennoch am Ende ein Nullsummenspiel herauskommt. Erblicke ich in einer Permanenz also die Figur "211" und habe mich vergewissert, daß zuvor weder "111" noch "112" erschienen sind, sollte ich mich ab da in jenem 87,67%-Bereich befinden, in dem "211" schneller ist. Die Betrachtungsstrecke reicht von hier aus bis entweder "111" oder "112" erscheinen. Beide zusammen sorgen für einen Couprückstand zu "211" (in dieser Stichprobe) mit 90.651 + 670 = 91.321 Beide schließen die Betrachtungssequenz mit ihrem Erscheinen ab, und haben am Ende dreimal hintereinander gewonnen. Also: 13.151 ("211" zu "111") + 11.320 ("211" zu "112") = 24.471 24.471 x (+)3 = 73.413 91.321 (Coupvorsprung) - 73.413 (ununterbrochenes dreimaliges Treffen) = 17.908 Coups bleiben somit als Coupmenge des unbekannt-unerforschten übrig. Im Hinblick auf die 2 x 15.000 = 30.000 Anzahl der hier betrachteten Fälle, wird deutlich, wie dünn die Luft ist, wo sich eventuell etwas Interessantes ereignen könnte. Gruss elementaar -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Das sehe ich vollständig anders. Buchstäblich jeden Text so fehlerübersät rauszurotzen, daß jeder "Oberlehrer" lieber den Beruf wechselt, als sich an die Korrektur zu machen, drückt eine Verachtung möglicher Leser aus, wie sie größer nicht sein könnte. Sich, darauf angesprochen, auch noch weigern, wenigstens ein Rechtschreibeprogramm zu benutzen (eines steht ja mit der Forensoftware sowieso zur Verfügung), kennzeichnet diese Verachtung als vorsätzlich. Jeden Korrekturversuch als nicht hinnehmbaren Angriff auf die Person zu betrachten, ist rational nicht nachvollziehbar. Niemand muss SEINE täglichen Herabsetzungen, missgünstigen Vermutungen und Beschimpfungen dulden. In jeder anderen Gesellschaft wäre ER schon längst hochkantig und auf Lebenszeit rausgeflogen, allein für den Unrat, den ER täglich hier ablädt. Und es ist schon mal gar nicht erbärmlich, wenn man darauf besteht, daß zwei eben nicht drei und auch nicht vier ist. Das ist Grundlage jeden sinnvollen Gesprächs. Überhaupt darauf hinweisen zu müssen, ist abschreckend und verstörend genug. -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
In welchem Bereich der Phantastik wir uns befinden, macht auch eine Überschlags"gegen"probe deutlich. Laut der kürzlich von @Ropro eingestellten Gegenüberstellung https://www.roulette-forum.de/topic/31153-favoritenangriff-nach-bin-öffentliches-testspiel/page/29/#comment-516872 hat ER in 67 Sätzen mit durchschnittlich 7,12 gesetzten Zahlen 12 (wahrgewordene) Treffer erzielt. Mit grob 68,5% Umsatzrendite hätte ER zu diesem Zeitpunkt aber schon 22 echte Treffer erzielen müssen. IHM fehlen also zu diesem Zeitpunkt schon deren 10. Für ein Spiel mit 68,5% Umsatzrendite segelt ER damit schon wieder stramm Richtung -3 sigma. -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Ich bin entschlossen, wenigstens dieses eine Mal nicht zurückzuwinken, auch wenn das unhöflich wirkt. -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Entgegen @jasons zum Schild gewordener, nur zu wahren Einsicht (danke!): Zum ersten Dreck: Die eingestellte Tabelle ist nicht "abgeschrieben", sondern nach SEINEN Angaben (Signifikanz nach 30.000 Sätzen) extra für IHN angefertigt. Die Werte sind, wie oben geschrieben, nach der Clarius-Formel extra für IHN gerechnet. Clarius wird im Hallerschen Lexikon unter "Clarius, Wolfgang L., Diplom-Physiker" aufgeführt. Dort oder in dem anderen dicken Haller-Buch wird auch dessen Formel zur Signifikanz von Glücksspielergebnissen aufgeführt, und wenn ich mich recht erinnere, ausführlich erklärt. Bitte dort nachlesen. Wenn ich mich weiter recht entsinne, ist die Formel in mindestens einem der beiden Bücher mit einem (offensichtlichen) Druckfehler behaftet. Geht es nur um die pure Formel, kann ER auch diesem Link (zum zweiten Mal hier erwähnt) folgen: https://www.roulette-forum.de/topic/1250-ab-wann-ist-ein-system-gewinnsicher/ wenn es nicht zu viel Arbeit macht. Mit dem "Taschenrechner", egal welcher Provenienz, muss ER dann aber SEHR sorgfältig damit sein, wann ER welche Taste drückt - bei Fehlern kommt nur Unsinn raus. Wie auch der "Chi-Quadrat"-Test, (den ER trotz ausdauernder Hilfe von @Ropro auch nicht verstanden hat), versucht auch die Clarius-Formel zur Signifikanz eine Antwort darauf zu geben, wie lange eine Strategie an echten Zufallszahlen getestet werden muss, bevor die Nullhypothese der reinen Zufälligkeit verworfen werden kann. Es ist hier die Rede von begründbaren Argumenten, nicht von Geschwätz. Für eine wirkliche "Erklärung" stehe ich bei IHM nicht zur Verfügung. Was schon bei dem einfachen Chi-Quadrat-Test nicht klappt, wird bei "Clarius" gewiss nicht funktionieren, zumal ja an jeder Ecke die Einflüsterungen des "math." zu befürchten sind; dann ist eine "Erklärung" sowieso unmöglich. Ja. Ganz unironisch: Glückwunsch. Das ist schön. Und das ist genau die Frage nach der Signifikanz. Nämlich: Wie werden die nächsten 30.000 Satzcoups mit demselben Ansatz ausgehen? Bei einem Plein-Spiel (und lassen wir die Satzhöhenvariation beiseite: im Gleichsatz) sind eben viele weitere 30.000er-Pakete zu testen, bevor von einem "gewinnfähigen Spielansatz" mit Signifikanz gesprochen werden kann. Oder aber ER muss in den vergangenen 30.000 Satzcoups eine Umsatzrendite in der Höhe erzielt haben, wie sie die Tabelle ausweist. Übrigens: Das mehrmalige Quadrieren innerhalb der Clarius-Formel führt regelmäßig dazu, daß die Anzahl der zu testenden Satzcoups explodiert, wenn nur einer der restlichen Parameter geändert wird. Bei gleicher Umsatzrendite und einer Verkleinerung der Restunsicherheit um die Hälfte, vervierfacht sich die Anzahl der zu testenden Satzcoups. Dasselbe geschieht, wenn die Umsatzrendite doch nicht ganz so hoch ist wie erwünscht, oder doch mehr Zahlen pro Satz gesetzt werden müssen. So, mal wieder "viel" Text, aber auch viel Inhalt, so man sinnerfassend lesen kann. -
Favoritenangriff nach BIN- öffentliches Testspiel
topic antwortete auf elementaar's Sven-DC in: Tendenzspiel und Persönliche Permanenz
Aha, das ist ja wenigstens mal eine konkrete Angabe. Der Dank dafür fällt äußerst schmallippig aus, da ER ja weiter mit Dreck um sich wirft. Die benötigten Umsatzrenditen (Clarius, 3 sigma, 10% Ungenauigkeit) sind dann: Lesebeispiel: Um nach ca. 30.000 gesetzten Coups ein Signifikanzniveau mit der angegebenen Sicherheit und einer durchschnittlich bespielten Chancengröße n=7 zu erreichen, ist eine Umsatzrendite von 68,5% nötig. -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
Vielen Dank an @Feuerstein! Mit dieser erfreulich simplen Methode komme ich dann zu diesem Befund: Damit wäre dann wenigstens die Frage nach der Reproduzierbarkeit geklärt. Gruss elementaar -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
Spielt man mit dieser Programmierung https://penneys.github.io/ ein wenig herum, dann wirft die Maschine (Coup für Coup) so lange, bis einer der Spieler seine Sequenz vollständig gewonnen hat, und schreibt dem Gewinner in der Ergebnisliste +1 gut. Übersetzt in ein 36er-Roulette: die Partie ist zu Ende, sobald einer der Spieler drei mal in Folge getroffen hat. Beide Spieler können somit erst zum zweiten Satz ihrer Sequenz gelangen, wenn sie ihren jeweils ersten Satz gewonnen haben. Zum jeweils dritten Satz ihrer Sequenz kommen sie erst, wenn sie die beiden vorherigen gewonnen haben. Bei Fehltreffer müssen sie wieder mit Position 1 ihrer Sequenz beginnen. Wie viele Plus und Minus sie auf dem Weg dahin machen, ist ungewiß. Da man als Roulettespieler aber nicht gegen einen anderen Spieler, sondern gegen den Bankhalter antritt, ist das dann aber doch eine nicht ganz unwichtige Information. Beim Übertrag des Spiels auf das 36er-Roulette hat @Feuerstein auf jeden Fall mit seinem Einwand recht, daß nicht gegittert werden darf. Gruss elementaar -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
Hallo @Hans Dampf (von), Dieses Mal leider nicht, was aber kein Grund ist, nicht weiter zu buddeln, vielen Dank. Wie oben vermerkt, habe ich mich bei den Auszählungen nach diesem https://en.wikipedia.org/wiki/Penney's_game Eintrag orientiert - die Tabelle habe ich benutzt, um Spieler2 zu sagen, was er nach Ansage von Spieler1 zu spielen hat. Die Spalte "Quoten zugunsten des 2. Spielers" habe ich ganz naiv mit der Bedeutung "Häufigkeit" belegt (bspw. Zeile 1 Quote "7 zu 1" würde bedeuten: Spieler2 ist sieben mal (Anzahl) schneller fertig als Spieler1). Das war vielleicht falsch. Bevor ich an die Einrichtung der Auszählungsroutine ging, habe ich per startpage-Rundruf gleich eine Reihe von Aufsätzen entdeckt und heruntergeladen, wo sich, bestimmt viel klügere Leute als ich es bin, mit dem Phänomen befassen. Mein erster Eindruck ist der, daß doch einige Leute davon fasziniert sind. Die gründliche, persönliche Lektüre steht allerdings noch aus. Zuerst wollte ich möglichst schnell und einfach wissen, ob es sich überhaupt rentiert, sich per Roulettezahlen mit dem Phänomen zu befassen, oder ob es sich um eine, immer mal wieder auftauchende, Fata Morgana handelt (die Zahlen spiegeln etwas vor, was sich praktisch nicht nutzen läßt). Aus meiner Sicht (als ausgewiesener Faulpelz, leider) deuten die Befunde auf nötige weitere Arbeit hin. Gruss elementaar -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
Hallo @Ropro, Du hast ja Recht. Zweifellos enthält das 37er-Roulette die spielwirksame Zahl "Zéro". Und wiederum zweifellos muss man damit im praktischen Spiel zurecht kommen. Da kann ich zum jetzigen Zeitpunkt, falls wir es weiterverfolgen, nur um Geduld bitten. Penney wirft nämlich mit Münzen. Da gibt es "Zéro" nicht. (Wenn einmal eine Münze auf der Kante stehen bleibt, ist es einfach kein korrekter Wurf, da definitionsgemä0 nur "Kopf" oder "Zahl" gültige Ergebnisse sind.) Zur Beschreibung und Betrachtung des Phänomens mit Roulettezahlen muss also "Zéro" zwingend ausgeschlossen sein, sonst ist es kein gültiges Äquivalent zum Münzwurf. Ob überhaupt und, wenn ja, wie sich noch zu erwerbende, weil zur Zeit nicht vorhandene Erkenntnisse der Betrachtung, in ein reales Roulettespiel übertragen lassen, liegt noch in weiter Ferne. Wie schon bei "vdW" nach einem ausgiebigen Betrachten der Eigenschaften des Phänomens, gelingt vielleicht auch hier die Integration von "Zéro" (s. vdW zwei Farben --> drei Farben mit asymmetrischen EW). Falls sich diese Frage nach der Betrachtung überhaupt noch stellt. Gruss elementaar -
Eine Frage zu Reihen
topic antwortete auf elementaar's chrisR in: Statistik, Abkürzungen, Phänomene, Mathematik
Hallo @Feuerstein, da stimmt was nicht, ich muss selbst erst mal nachlesen... Die Verwirrung könnte ich verursacht haben. Nach dem Einstellen des ersten Beitrags (mit rollierender Gitterung) bemerkte ich einige Fehler, die mich veranlassten, den ganzen Beitrag mit Platzhalter zu entfernen und gründlich zu überarbeiten; ca. zwei Stunden später habe ich die überarbeitete Fassung wieder eingestellt (und dies in "Grund der Änderung" vermerkt.) Ich bitte um Entschuldigung für die evtl. angerichtete Verwirrung, die sich im aktuellen Fall aber kaum vermeiden ließ, denn Fehler müssen ja verbessert werden. Gruss elementaar