Ivoire
Mitglieder-
Gesamte Inhalte
184 -
Benutzer seit
-
Letzter Besuch
Inhaltstyp
Profile
Forum
Kalender
Articles
Alle erstellten Inhalte von Ivoire
-
"...man verliert beim "ungeraden Marsch" bei jeder geraden Serie zwei Stücke und gewinnt 1 Stück bei einer ungeraden Serie. Fazit: Mit dem ungeraden Marsch gewinnt man auf keinen Fall, wenn man immer in gleicher Satzhöhe spielt."
-
Suche Excelprogrammierer!
topic antwortete auf Ivoire's Luksz in: Excel Formeln und Makros, Programmier-Lehrgänge
Sehr schön. Das klingt nach der zwingenden Benutzung von Makros (VBA). Sehr zeitaufwendig. -
Suche Excelprogrammierer!
topic antwortete auf Ivoire's Luksz in: Excel Formeln und Makros, Programmier-Lehrgänge
Um welche Spielidee geht es überhaupt? -
Mit Sicherheit nicht. Das wurde schon vielfältig untersucht. z.B. http://www.excelfunktionen.de/base/id_21.php Ein Trick, damit es nicht nicht sofort eine VBA-Code Lösung sein muss. Baue in deine Zufallsformel die Zeit =Jetzt() ein. Du startest die Zufallserzeugung immer zu einem anderen Zeitpunkt, damit dürfte nie die gleiche Zufallsreihe erzeugt werden. Oder noch raffinierter: Nimm eine originale Jahrespermanenz von ca. 100.000 Coups und springe mit einer Zufallszahl immer wieder an eine Stelle, aber der dann deine zu untersuchende Zahlenmenge beginnt.
-
Sowas schreibt man, wenn man das nie ausgetestet hat. Erzähl doch bitte, wieviel Jahrespermanenzen du mit Excel durchgetestet hast. Hast du z.B. schon mal geprüft was passiert, wenn man die d'Alembert-Progression so streckt, dass man erst den Einsatz erhöht, wenn man per Saldo 10 Coups verloren hat? Das wird ein sehr langwieriges Spiel, dürfte man nicht in einer Tagessitzung beenden können. Aber es reicht doch schon, wenn man nach einer Handvoll Tagessitzungen wieder im Plus ist. Setz dich an eine Tabellenkalkulation und teste es aus. P.S. Aus wievielen Coups besteht denn deine Tagessitzung? Ich hatte 111 vorgeschlagen, man kann aber auch 8 Stunden à 30 Coups spielen, also 240.
-
Würdest du das bitte mal voll und ganz überschauen. Du möchtest jeden Tag garantiert ein Stück gewinnen, das geht. Indem man entweder mit der Martingale jeden Tag grundsätzlich gewinnt, bei wahnsinnigem Kapitalbedarf oder indem man im Monat per Saldo 30 Stücke gewinnt, bei sehr stark gestreckter Progression, meinetwegen die Déance. Spiele auf das, was garantiert in einer Tagessitzung (z.B 111 Coups) vorkommt, oder was garantiert mal in einer Woche (777 Coups) vorkommt oder meinetwegen im Monat (also 30x111 Coups) mit entsprechend angepasster Progression.
-
Sieh das bitte nicht so. Bei 360 Tagespartien wird es einfach den schlechtesten Tag im Jahr geben, genauso wie den besten. Du wirst trotzdem gewinnen, weil du genug Kapital bei dir hast. Die Angst-Tage auf einen einzigen Tag zu reduzieren habe ich tatsächlich schon mal in der Praxis erlebt. Ein Gast betritt das Casino, geht zu Kasse und legt dann das Maximum auf eine einfache Chance, und? Natürlich kam Zero. Nach zwei weiteren Coups hatte er dann sein Kapital verdoppelt und raus. Dieses Spiel ist zwar extrem kurz, aber nicht zu empfehlen.
-
Nein, es gibt keine verflixten Tage und keine Verlustobergrenze. Du musst es so verstehen: Wieviel Kapital braucht man, um den schlechtesten Tag im Jahr zu überleben? Ich sage dir, die benutzte Progression kann gar nicht flach genug sein. Also nicht mit einem Platzer abbrechen und meinen, dass holt man in den nächsten Tagen schon wieder auf. Und es klingt doch eigentlich idiotisch: Man hat 10000 € in der Tasche und soll sich mit 30 € pro Tag zufrieden geben?
-
Ganz und gar nicht ausreichend. Mal locker ca. 100 Tage durchgetestet und ab ins Casino. So geht es nicht. Beim Durchtesten eines Systems geht es darum, den Kapitalbedarf für die schlechteste Partie zu finden. Zum Beispiel so: Man betritt an 360 Tagen im Jahr ein Casino und bespielt immer exakt 111 Coups (sind genau 3 Rotationen). Wieviel Kapital muss man nun vorhalten, damit man auch die schlechtesten Tage überlebt? Ein erfolgreiches System für dieses Jahrespiel würde so aussehen: Man nimmt immer 10000 € mit, begnügt sich jeden Tag mit 30 € Gewinn, hat nach einem Jahr dann 30*360=10800 € gewonnen, also sein Kapital im Jahr verdoppelt. An den 3 schlechtesten Tagen hat man das gesamte Kapital von 10000 € benötigt, um wieder ins Plus zu kommen. An den 3 besten Tagen, es sind eigentlich noch mehr, geht man sofort mit dem vorgegebenen Gewinn von 30 € aus dem Casino. So läuft das Gewinnen beim Roulette.
-
Ich bin etwas falsch verstanden worden. Es ging mir hier nicht um einen "Tipp für ein Dauergewinnsystem". Ich habe keine "Rückholkraft" aufzeigen wollen. Es ging mir nur um den "Kniff", einem schlechten Permanenzverlauf zu glätten. Was ich ausdrücken wollte: Partien, die mit Ergebnissen wie +1/-2, +1/-3, .... +1/-10 enden, haben ein anderes Serienverhalten an gewonnenen und verlorenen Partien. Kann man alles ermitteln, wenn man es versteht, mit Tabellenkalkultationen umzugehen. Und dieses Serienverhalten von gewonnenen/verlorenen Partien eröffnet einem eine viel geschicktere Art von Progression, die halt im Verlustfall die Rückholkraft darstellt. P.S. Händische Prüfungen von Permanenzen am Küchentisch sind lächerlich.
-
Das geht ganz anders als der Ansatz, den du verfolgst. Du verfolgst die Methode, viel mehr Chancen zu belegen, dadurch gewinnt man zwar häufiger, aber ein Vorteil bringt das erst mal nicht. Man kann nach Belieben seine Gewinnhäufigkeit einstellen, indem man partienweise spielt. Wie geht das? Alle betrachten hier nur den Coup, den sie gerade gesetzt, gewonnen oder verloren haben. Statt dessen kann man aber auch mehrere Coups auf einmal betrachten, die dann eine Partie bilden, die gewonnen oder verloren wurde. Mal angenommen, eine Partie ist definiert, dass sie immer aus zwei Coups besteht. Dann sind die Partieergebnisse "RR","RN";"NR";"NN" möglich. Wenn man z.B. nur auf Rot spielt, dann verliert man bei einer 20er Serie auf Noir 10 Partien. Also mehr als 10 Verlustpartien hintereinander sind nicht wahrscheinlich, zumindest keine 20 Verlustpartien wie sie bei coupweisen Spiel möglich sind. Aber es geht noch viel raffinierter. Man definiert eine Partie nicht durch ihre Länge, sondern durch ihr Ergebnis. Z.B. Eine Partie ist beendet, wenn man +1 Stück gewonnen hat oder -2 Stücke verloren hat. Egal vorauf man setzt, ob mit Marsch oder Bauchgefühl, bei vollständigem Ausgleich wird man 2 mal soviel Gewinnpartien haben, wie Verlustpartien. Es geht noch krasser. z.B. eine Partie ist beendet, wenn man -10 Stücke verloren oder +1 Stück gewonnen hat. Was passiert dann mit dieser berüchtigten 20er-Serie ? Man hätte schlimmstenfalls 2 Verlustpartien hintereinander und viele, viele, bei vollständigem Ausgleich 10 mal so viele Gewinnpartien. Also wie man sieht, kann man sich das Verhältnis von gewonnenen und verlorenen Partien nach Belieben einstellen. Was bringt das Ganze ein? Ein viel geschickteres Vorgehen, um die Verlustpartien durch Satzsteigerung zu egalisieren. P.S. Jetzt aber genug der Tipps, sonst fangen hier noch einige an zu gewinnen.
-
Das Seriengesetz gilt auch für "Serien von Serien"
topic antwortete auf Ivoire's Ivoire in: Roulette Strategien
Excel und die Computerpower von 2007 waren nicht der Lage, mal eine Jahrespermanenz von über 100.000 Coups zu verarbeiten. Das geht erst heute. Allerdings verfügen hier viele User nicht über grundlegende Excelkenntnisse. Noch ein paar Anmerkungen. Die zweite Tabelle mit den Serien von Serien bezieht sich auf Schwarz/Rot. Dieser Ausreißer bei den 10er Serien ist korrekt. Zero wurde innerhalb einer Serie nicht gewertet. Kurt von Haller hätte da gerne unterschieden zwischen soziablen und solitären Häufigkeiten, aber es ist satzmäßig nicht sinnvoll bespielbar, wenn eine neue Serie auf der gleichen Chance beginnt. Am Ende der Jahrespermanenz kann es dazu kommen, dass Serien von Serien noch nicht in der Länge bestimmt sind, weil noch keine höhere Serie erschienen sind. Das Ganze kann man weiter betreiben. Wie häufig kommt denn z.B. eine Nase auf den Intermittenzen vor, bis endlich eine Intermittenzkette erscheint? Auch solche Intermittenznasen können in einer Anhäufung/Serie vorkommen. Wie lang werden denn die? All das habe ich ausgewertet. Jeder möge sich selber damit beschäftigen. -
Das Seriengesetz gilt auch für "Serien von Serien"
ein Thema hat Ivoire erstellt in: Roulette Strategien
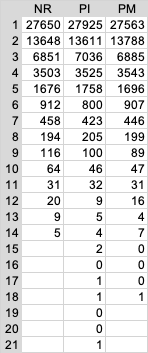
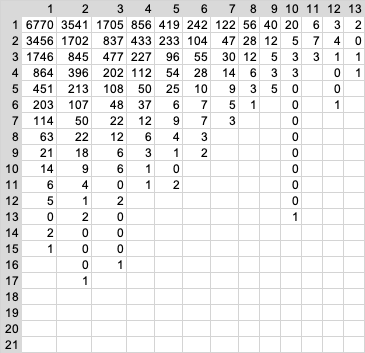
Ich möchte mal etwas darstellen, was so noch nicht in der Literatur zu finden ist. Das Seriengesetz gilt auch für Serien von Serien. Was ist darunter zu verstehen? Das Seriengesetz für die einfachen Chancen besagt, dass es genauso viel Einer-Serien gibt, wie höhere, genauso viel Zweier-Serien wie höhere, genauso viel Dreier-Serien wie höhere, usw. Und weil das so ist, gleicht sich alles ideal aus. Einmal idealisiert dargestellt, gibt es bei 1024 Einer-Serien 1024 Einer-Serien (Intermittenzen) 512 Zweier-Serien 256 Dreier-Serien 128 Vierer-Serien 64 Fünfer-Serien 32 Sechser-Serien 16 Siebener-Serien 8 Achter-Serien 4 Neuner-Serien 2 Zehner-Serien 1 Elfer- oder höhere Serie An an Jahrespermanenz überprüft sieht das so aus: Jahrespermanenz Hamburg 1999 (insgesamt 113678 Coups): Nun können sich auch Serien anhäufen, quasi in Serie auftreten. Am einfachsten sieht man das bei Intermittenzen. Diese Anhäufungen bezeichnen manche als Intermittenzketten. Kurt von Haller hatte die so genannt. Kommt eine Intermittenz solitär zwischen zwei höheren Serien vor, spricht man von einer Nase oder Coup de Lion. Wenn mehrere Intermittenzen hintereinander auftreten, nennen wir es halt Intermittenzkette. Bei höheren Serien, 2er, 3er, 4er usw. ist mit einer Serie (Anhäufung) gemeint, dass sie sich solange anhäufen, bis eine höhere Serie das beendet. Also eine Serie von 4er Serien wird beendet von einer 5er, 6er oder höheren Serie. Zwischen den Vierer auftretende 1er, 2er, 3er Serien werden nicht beachtet. Für obige Jahrespermanenz habe ich auch mal die Anzahl dieser Anhäufungen von Serien ermittelt: Also eine Nase kommt 6770 mal vor, die längste Intermittenzkette ist 15 Intermittenzen lang. Eine 2er Serie kommt 3541 mal solitär zwischen höhreren Serien als zwei vor. Höchsten jedoch 17 mal, das kann aber bedeuteten, das zwischen diesen vielen 2er-Serien auch Intermittenzen vorkommen können. Die werden nicht beachtet. Wer diese Tabelle genau studiert, dem erschließt sich schnell eine ganz einfache Gewinnstrategie (mit Progression, die nicht in den Himmel wächst). Viel Erfolg beim Gewinnen. -
Kann man eine Permanenz so umformen, dass nicht mehr so große Ecarts, wie sie eigentlich in einer Permanenz vorkommen, auftreten? Das geht, widerspricht aber der Logik. Wir nehmen die Jahrespermanenz eines Roulettekessels im Casino Hamburg aus dem Jahre 2000 mit 118.931 Coups. Ein bisschen Programmiererei in Excel später haben wir die Serienhäufigkeit ermittelt: 1 28919 2 14484 3 7137 4 3690 5 1794 6 924 7 436 8 227 9 128 10 56 11 24 12 12 13 7 14 2 15 0 16 2 17 0 18 0 19 1 Wie man sieht, die höchste vorkommende Serie war einmal eine 19er Serie. Man betrat das Casino, sah die Permanenzanzeige und staunte an dem Tag nicht schlecht, als 19 mal hintereinander die gleiche Farbe vorkam. Nun machen wir aus dieser vollständigen Originalpermanenz zwei Permanenzen, die ich Teilpermanenzen nennen möchte. Die erste Teilpermanenz besteht aus dem 1. , 3. , 5. , 7., ....usw. Coup. Die zweite Teilpermanenz bildet sich dann aus dem 2. , 4. , 6. , 8. , .... usw Coup. Es versteht sich von selbst, dass beide Teilpermanenzen gleich lang sind, und die zweite Teilpermanenz erst einen Coup nach dem ersten Coup überhaupt beginnt. Ich behaupte nun, dass auf diesen beiden Teilpermanenzen die Ecarts nicht so groß werden, wie in der vollständigen Originalpermanenz. Warum soll das so sein? Logisch betrachtet steht jeder Coup für sich allein. Die Kugel hat kein Gedächtnis, sie speichert nicht, in welchem Fach sie zuvor gefallen ist. Was muss denn passieren, damit auf einer Teilpermanenz auch die längste Serie der Originalpermanenz, die 19er, vorkommt? Dann müsste in der Originalpermanenz eine 38er Serie vorkommen, und man hätte auf beiden Teilpermanenzen eine 19er Serie auf der gleichen Farbe. Es geht auch noch anders, es könnte auch während 38 Coups nur Intermittenzen erscheinen. Dann hätte man auf den beiden Teilpermanenzen auch zwei 19er Serien, in der einen Teilpermanenz auf rot in der anderen auf schwarz. Selbst lange Serien während 38 Coups, immer mal unterbrochen durch eine Intermittenz (Nase) die auf der anderen Teilpermanenz landen sollte, würde zumindest auf einer Teilpermanenz eine 19er Serie erzeugen. Schauen wir mal, wie die Serienhäufigkeit auf den beiden Teilpermanenzen aussieht, und beide zusammenaddiert. 1 14433 14441 28874 2 7273 7305 14578 3 3569 3600 7169 4 1826 1804 3630 5 937 940 1877 6 459 446 905 7 229 213 442 8 103 111 214 9 50 63 113 10 22 26 48 11 15 13 28 12 3 3 6 13 2 3 5 14 0 0 0 15 3 0 3 16 2 1 3 17 1 1 Es fällt einem nicht sofort auf, ein gewisses Ausbleiben von hohen Serien könnte man erkennen. Doch signifikant ist das nicht. Immerhin kommt auf einer Teilpermanenz noch eine 17er Serie vor, aber dadurch, dass nach einer langen Serie auch viele Intermittenzen folgen. Wie sähe das ganze in einem Diagramm aus? Wir fangen bei Null an, immer wenn Schwarz kommt, bedeutet das +1 und bei Rot -1. Fortlaufend addiert ergibt sich dann eine Graph, ein Börsianer würde sagen ein Chart. Wir stellen nun den Graphen der Originalpermanenz und der Teilpermanenzen in einem Diagramm dar. Wenn z.B eine lange Streckenabschnitt von schwarzen Serien in der Originalpermanenz vorkommt, dann steigen die Teilpermanenzen entsprechend, jede für sich betrachtet nur halb so schnell. Kommt eine lange Intermittenzreihe, dann ergibt das auf der einen Teilpermanenz eine lange Serie auf Rot und auf den andern auf Schwarz. Gibt es einen gewissen Ausgleich durch lange Serien auf Rot, dann folgen die Teilpermanenzen entsprechend. Gesamt betrachtet schwanken die Teilpermanenzen nicht so stark wie die Originalpermanenz, sie verlaufen flacher, daher mein Titel, die flachen Teilpermanenzen, die mich zur These verleiten, dass dort die Ecarts nicht so groß werden. Das Ganze war hier nur die Grundlage für diese These. Richtig interessant wird es, wenn man eine Originalpermanenz in 3, 4, 5 oder sogar 10 Teilpermanenzen zergliedert. Also man schreibt die Permanenz quer, bespielt sie aber vertikal. Alle Teilpermanenzen verlaufen flacher, die Schwankungen einer Teilpermanenz werden nie größer sein, als bei der Originalpermanenz, sie führt kein Eigenleben. Was bringt das nun fürs praktische Spiel ein? Wo immer die Abweichungen (Ecarts) nicht so groß werden, könnte es einen Platzer vermeiden und eine Progression nicht zu stark steigen lassen.
-
Dazu kann ich nichts sagen. Jegliches Spielen als einziger Gast war mir suspekt. Das lag vor allem auch an den mangelnden Deutsch des ganzen Personals. In Karlsbad wird praktisch kein Deutsch gesprochen. Und mit dem Tschechischem kam ich überhaupt nicht zurecht.
-
Im August 2019 war ich im Casino im Pupp von Karlsbad. Um 20:30 Uhr war ich der erste Gast an einem Samstag Abend. Vollkommen leer, gelangweilte Croupiers, die ja nichts zu tun hatten. Eine Stunde später hatte sich die Gästezahl auf ein halbes Dutzend erhöht, ohne meine Person.
-
Bei einer realen Jahrespermanenz mit 118.931 Coups kommt es zu 3346 Wiederholungen. Im Durchschnitt sollte jeder Zahl 3214 mal vorgekommen sein.
-
Hilfe bei der Erfassung von Zahlenfolge in Excel
topic antwortete auf Ivoire's Manu91 in: Excel Formeln und Makros, Programmier-Lehrgänge
Wo liegt eigentlich dein Problem? Nimm die Excel Funktion https://support.office.com/de-de/article/zählenwenn-funktion-e0de10c6-f885-4e71-abb4-1f464816df34 -
Entschuldigung. Wurde von mir korrigiert.
-
Hiermit möchte ich mal einen Marsch auf einfachen Chancen vorstellen, der mir schon seit Jahren die Grundlage für ein erfolgreiches Spielen bildet. Dieser Marsch wird nirgendwo beschrieben, allenfalls schon mal als "springender Marsch (Sauteuse)" bezeichnet, ohne dass er genauer beschrieben wird. Ich bezeichne meinen Marsch mal als "Ungeraden Marsch". Er hat die Eigenschaft, dass man alle ungeraden Serien gewinnt, also alle Einer-, Dreier-, Fünfer-, Siebener-, Neuner-Serien, usw. Die Intermittenzen bezeichne ich in diesem Zusammenhang als Einer-Serie, sie haben auch eine ungerade Anzahl. Wird mit gleich großer Stückzahl gespielt, was auch als Masse égale bezeichnet wird, so bringt beim ungeraden Marsch jede ungerade Serie einen Gewinn von einem Stück. Das kann sehr schnell gehen, wenn sich Intermittenzen anhäufen. Alle gerade Serien, wie Zweier-, Vierer-, Sechser-, Achter-, Zehner-Serien, usw. bringen beim ungeraden Marsch einen Verlust von zwei Stücken, beim Spiel mit gleicher Satzhöhe. Die Satzweise ist ganz einfach. Ist die vorhergehende Chance seit Auftreten der Gegenchance in einer ungeraden Anzahl vorgekommen, so wird gegen die vorhergehende Chance gesetzt. Ist sie in einer geraden Anzahl vorgekommen, so wird die vorhergehende Chance gesetzt. Ein Bespiel: R S R R R S R S R R S S R + + - + + + + + - - - - Das Seriengesetz für die einfachen Chancen besagt, dass es genauso viel Einer-Serien gibt, wie höhere, genauso viel Zweier-Serien wie höhere, genauso viel Dreier-Serien wie höhere, usw. Und weil das so ist, gleicht sich alles ideal aus. Einmal idealisiert dargestellt, gibt es bei 1024 Einer-Serien 1024 Einer-Serien (Intermittenzen) 512 Zweier-Serien 256 Dreier-Serien 128 Vierer-Serien 64 Fünfer-Serien 32 Sechser-Serien 16 Siebener-Serien 8 Achter-Serien 4 Neuner-Serien 2 Zehner-Serien 1 Elfer- oder höhere Serie Wenn man nun aus dieser Aufstellung die ungeraden und geraden Serien aufaddiert, so findet man exakt zwei Drittel ungerade Serien und zu einem Drittel gerade Serien. So muss das auch sein, sonst hätte der Spieler einen Vorteil. Wir halten uns noch einmal vor Augen, man verliert beim "ungeraden Marsch" bei jeder geraden Serie zwei Stücke und gewinnt 1 Stück bei einer ungeraden Serie. Fazit: Mit dem ungeraden Marsch gewinnt man auf keinen Fall, wenn man immer in gleicher Satzhöhe spielt. Wenn man aber nach dem Auftreten einer ungeraden Serie den Satz immer um ein Stück erhöht, dann holt man sich seine bisherigen Verluste viel schneller zurück, als dass man auf einen kompletten Ausgleich spielen würde, der keineswegs absolut eintreten muss. Es gibt zweifellos Permanenzabschnitte, bei denen es zu einer Anhäufung von geraden Serien kommt, so ca. 20 gerade Serien in Anhäufung. Um diese Verluste wieder auszugleichen, bräuchte man nun 40 ungerade Serien. Hat man allerdings moderat die Einsätze erhöht, so geht der Ausgleich viel schneller. Ich habe viele vollständige Jahrespermanzen auf allen einfachen Chancen untersucht. Der ungerade Marsch ist eine passable Satzweise in Zusammenhang mit einer moderaten Progression, um dauerhaft zu gewinnen.
-
Man nehme mal eine authentische Permanenz, die man im Jahr bespielen kann. Sagen wir 37.000 Coups. Das wären pro Tag, bei 360 Spieltagen im Jahr, 103 Coups, wohlgemerkt jeden Tag. Jede Zahl sollte 1000 mal vorgekommen sein. Der Zufall will es aber, dass einige Zahlen häufiger als 1000 mal und andere Zahlen weniger als 1000x erschienen sind. Für die Favoriten, also die Zahlen die häufiger als Durchschnitt vorgekommen sind, gilt, dass sie pro Rotation häufiger als 1x erschienen sind. Das bedeutet allerdings nicht, dass sie immer 1 x pro Rotation vorgekommen sind, sondern sie können auch mal eine Pause machen, die im Extremen bis hin zu 250 Coups betragen kann. Mit den sechs Spitzenreitern würde ein Spiel gelingen, indem man mindestens 35 mal auf diesen Favoriten setzt, und eine Pause macht, bis sie wieder erscheinen. Dass ich mal eine authentische Permanenz entdeckt hatte, wo der Doppelschlag auch so einen Favoriten darstellt, sei Zufall gewesen. Doch man halte sich vor Augen, es wird immer Favoriten geben, die über den Durchschnitt liegen. Und was Excel betritt: Zwar soll man rein theoretisch Millionen von Zellen füllen können, doch allein mit 100.000 Coups in einer Spalte und weiteren gefüllten Spalten zum Auswerten geht Excel so richtig in die Knie. Ein ständiges Auszählen von 100.000 Coups, welche Zahlen denn nun die Favoriten darstellen, ist kaum machbar.
-
Billig und unprofessionell. Ich rede grundsätzlich von einer authentischen Jahrespermanenz von schlappen 100.000 Coups. Deine Excel-Zufallszahlen von gerade mal 5000 Coups sagen nichts aus. Und man muss auch nicht sehr lange im Netz suchen, um heraus zu finden, dass die Zufallszahlen in Excel gar nicht so zufällig sind. Ich gebe dir einen Tipp: Nimm deine Zufallsformel und multipliziere sie mit der Zeit "JETZT()", und sieh zu, wie du das wieder auf eine Menge zwischen 0 und 36 hinkriegst.
-
Ich hatte das auch mal mit anhand einer Jahrespermanenz untersucht. Die ungünstigste Rotation hat exakt aller vorherigen Gewinne wieder aufgezehrt. Aber es geht auch auf Dauer erfolgreich: Man spiele exakt die vorherige Zahl en Plein mit 1 Stück, solange bis man 35 Coups lang keinen Gewinn erzielt hat. Mit anderen Worten, ein Spiel auf Doppelschlag. Ist wieder ein Doppelschlag erfolgt, spielt man weiter. Da ganze funktioniert, defínitiv. Es ist das gleiche Spiel, als würde man mit der selben Spielweise auf die Zahl spielen, die bereits am häufigsten vorgekommen ist.
-
Zunächst habe ich gesagt, mindestens einen Dreier, bei mindestens 163 ausfüllten Feldern. Häufig sind es viel mehr und es könnte auch ein Sechser sein. Ich mach mal eine andere Rechnung auf. Beim Lotto gibt es ja so tolle Voll- und Auswahlsysteme. Bei einem Auswahlsystem kann man 26 Zahlen ankreuzen, daraus werden 130 Felder generiert und du hast garantiert gewonnen, wenn 3 Zahlen aus deinen 26 ausgewählten gezogen wurden. Nun gibt es ja auch Spezialisten, die schaffen es, garantiert keine richtige Zahl bei 26 Auswahlzahlen angekreuzt zu haben. Die brauchen mit einem zweiten Schein nur die 26 (genau genommen 49-26=23) noch nicht ausgewählten Zahlen zu spielen. Dann haben die auf ihrem zweiten Systemschein 6 Richtige mit Zusatzzahl. Dass könnte 466.127 Euro Gewinn einbringen oder nur 200. Bei dieser ganzen Geschichte reden wir hier von einem Einsatz von ca. 200 Euro pro Ziehung. Also wer beim Roulette mehr riskiert ist dann beim Lotto besser aufgehoben.
-
Bleib beim Lotto. Dass man da immer verliert, fällt dort weniger auf. Es sei denn, man spielt insgesamt 163 Felder bei jeder Ziehung. Dann sind mindestens 3 Richtige dabei, bei jeder Ziehung. Wer diese Zahlenkolonnen haben will, kann mich gerne anscheiben.